基于STM32單片機的AES算法優化與實現

許韞韜，呂志剛，黃義國,2，李曉艷

(1.西安工業大學電子信息工程學院， 陜西 西安 710021；2.江蘇無線電廠有限公司，江蘇 南京 210012)

0 引言

當今社會，隨著時代的不斷進步，人類的科技生活已經逐步邁入信息化的時代。然而，人們在享受信息通信所帶來的便利和快捷的同時，難免會遇到信息泄漏或竊取事件，保障重要信息通信的安全性已逐漸成為社會關注的熱點。密碼學是保證信息通信安全的有效辦法之一，人們可以利用密碼學中的各種數據加密算法，對一些重要的數據信息進行加密處理，從而有效提高信息的安全防護能力，降低信息在通信過程中泄露的風險，有效保護人們的信息安全[1-2]。

在實際的加解密處理中，高級加密標準(advanced encryption standard，AES)是現階段通用的區塊分組式加密標準。其硬件實現方式相對于軟件實現，具有更高的物理安全性和運行速率。在密碼學中，對稱分組密碼算法能夠完成置換運算的基本結構就是S盒(substitution-box)。密碼學的不斷革新，推動了密碼破解技術的發展。由于各種攻擊方法相繼涌現，AES算法在密碼學的地位也受到了一定的沖擊。其主要原因在于，AES算法自身仍存在不足。諸如算法結構層次上具有一定的缺陷，加、解密的結構不對稱，擴展密鑰的安全等級不高等[3]。針對AES算法在密鑰擴展過程存在的不足，提出了一種優化方案，分別通過MATLAB仿真軟件和STM32處理器對優化后的AES算法進行了研究。該算法具有很好的安全性和可靠性。

1 AES算法及優化

1.1 算法概述

AES算法又稱Rijndael算法，是現階段加密方面使用最為廣泛的對稱分組式算法之一[4]。AES算法的制定是為了替代已被攻破的美國數據加密標準(data encryption standard，DES)算法。AES算法在算法結構上采用的是SPN結構，通過特殊迭代密碼，可以有效地抵御現有的多種密碼攻擊方式[5]。由此可見，AES算法的抗密碼能力要遠遠強于被淘汰的DES算法，同時AES算法還擁有良好的可擴展性。

AES算法作為現階段常用的對稱分組式加密算法，其明文分組的長度為128位。算法在加解密處理過程中所涉及的密鑰長度主要有AES-128、AES-192和AES-256三種，分別表示128位、192位、256位的密鑰長度。根據矩陣形式，使矩陣中的每個字節按照由上至下和由左至右的秩序進行排列，從而構成由16個字節組成的有序矩陣。通過這種方式，構成了AES算法分組的基本結構。AES算法對語音信息進行加密和解密的處理過程，其實質是由對應的矩陣進行相應的變化實現的。在矩陣進行變換的過程中得到的中間態稱為狀態矩陣。對這些狀態矩陣進行不同次數的迭代輪變換，可實現對信息的加密和解密處理[6]。根據密鑰長度的不同，AES算法在加密以及解密的兩個過程中[7]與之相應的所執行的迭代次數也不相同。三種加密算法的加密輪數如表1所示。

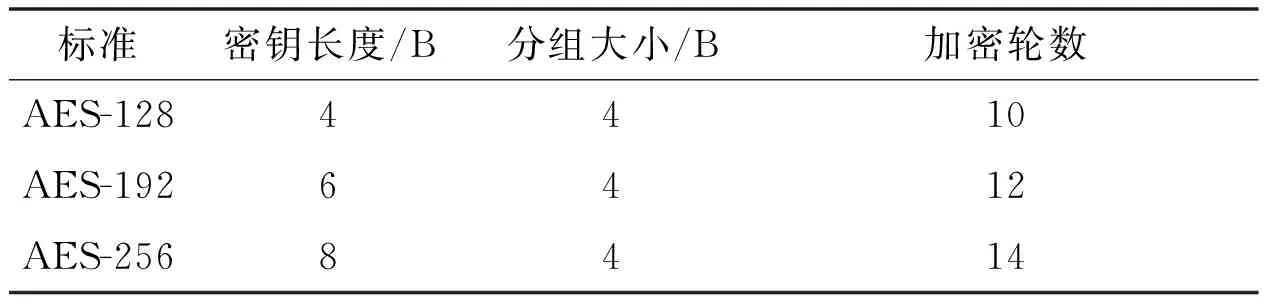
表1 三種加密算法的加密輪數

密鑰長度以及分組大小在運算過程中都是以字節為單位，而每個字節的長度為32位。AES算法在進行加解密的過程中，當使用的密鑰長度越長時，算法在加解密的過程中需要操作的加解密的輪數也會隨之變得更多。此時相應的算法安全性也變高，但缺陷是算法的運行效率會受到影響，解密所使用的時間變得更長。所以用戶需要根據實際的項目需求選擇合適的密鑰長度，達到相應的安全級別。由于語音數據量大、變化速率快，在確保AES算法的安全性的同時，實現盡可能高的執行效率。通過對幾種算法在運行效率以及算法安全程度的對比分析，最終選擇執行效率和安全性都相對較高的AES-128算法，實現對語音信息的加密以及解密操作。

1.2 密鑰擴展算法

利用初始密鑰進行迭代處理生成算法加解密所需要的子密鑰的過程就是密鑰的擴展。在這個過程中，需要用到密鑰擴展算法完成初始密鑰向子密鑰的轉換，然后將生成的子密鑰應用到算法的加解密過程中。選擇AES算法類型為AES-128，在完成一次明文向密文的轉換過程需要執行10輪運算。但是根據實際測試發現，運算速率還是無法滿足對語音數據的加密要求。通過查閱相關資料后，將10輪算法精簡至6輪運算，在保證算法安全性的基礎上，算法的運行速率也得到大幅提升。據此，AES算法完成6輪運算共產生896位密鑰。

假定選用Wi來表示密鑰矩陣K中的第i列對應的數值，根據密鑰擴展算法遞歸得到Wi的數值完全是由Wi-1和Wi-4決定的。AES算法在進行密鑰擴展的過程是依據式(1)和式(2)執行的。其擴展規則為：如果i的值不是4的整數倍時，只需要把Wi-1和Wi-4對應的數組進行異或變換就可以得到Wi；當i的數值為4的整數倍的時候，式(2)中的Wi-1需要通過函數“g”變換后得到結果，再將計算結果與Wi-4進行異或運算得到Wi。

Wi=Wi-4?Wi-1，i不是4的倍數

(1)

Wi=Wi-4?g(Wi-1)，i不是4的倍數

(2)

式中：Wi、Wi-1、Wi-4分別為密鑰矩陣K中的第i列、第(i-1)列、第(i-4)列所對應的矩陣。

AES算法在完成初始密鑰生成輪密鑰時要用到輪常量數組Rcon[i]。它是一個4×10常量數組，同時數組的每一列均含有4個字節。其中：Rcon[i]每列的高8位均是由數組RC[i]組成，余下的位都用0補充，即Rcon[i]=(RC[i],0,0,0)。密鑰擴展過程中的輪常量取值如表2所示[8]。

表2 輪常量取值

根據上述的密鑰擴展過程，以W0-3作為用戶設定的初始密鑰，通過密鑰擴展算法得到輪密鑰W4-7。密鑰擴展過程如圖1所示。

函數“g”是經過三個基本變換得到的復雜函數，即循環移位(RotWord)、字節代換(SubWord)和輪常量異或[11-12]。若輸入數據為W=(B0,B1,B2,B3)，通過RotWord變換后得到 (B1,B2,B3,B0)，再經過SubWord變換后得到(B1a,B2a,B3a,B0a)，最后通過與RC[i]異或運算得到g(W)，并將得到的結果g(W)運用于式(1)、式(2)的運算過程。

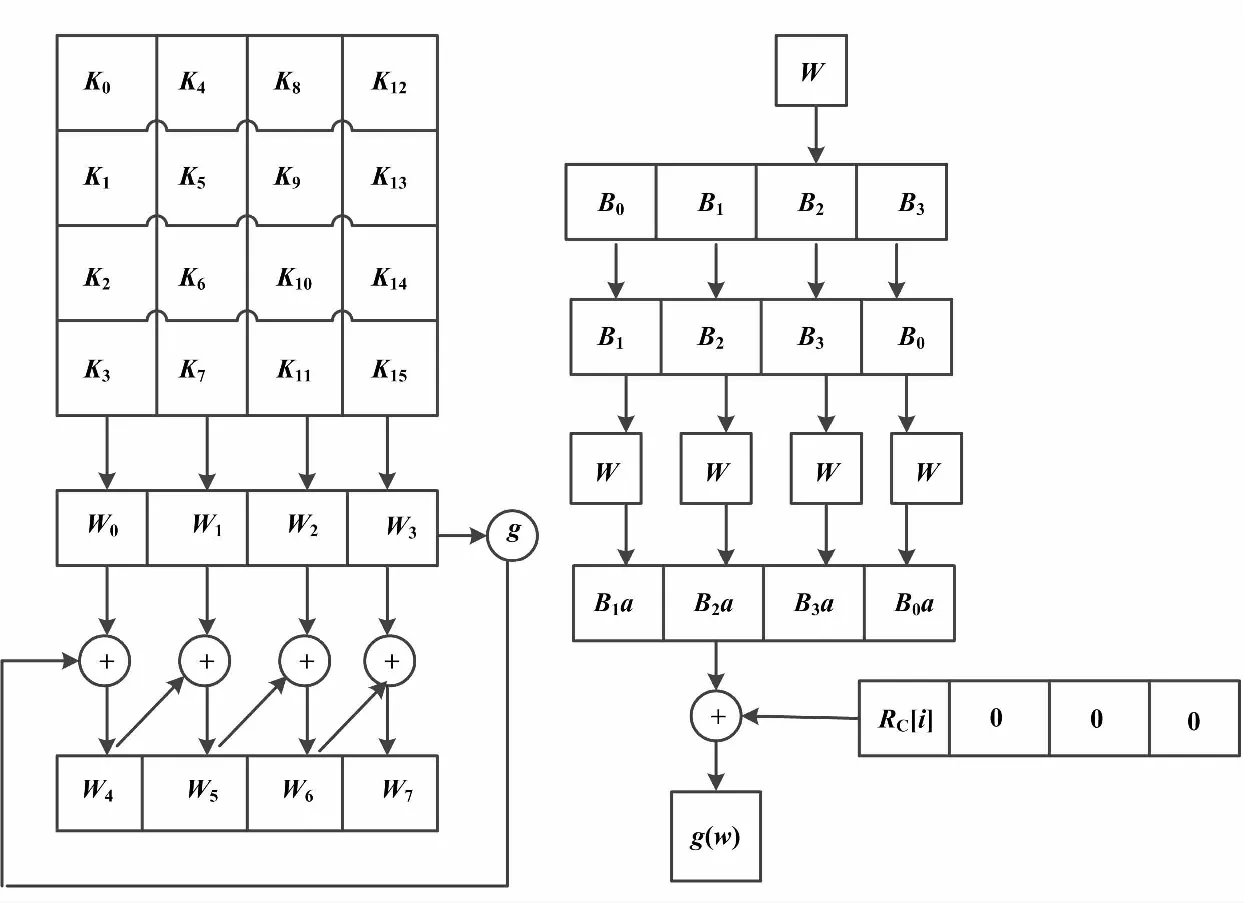
圖1 密鑰擴展過程圖

1.3 算法優化

在加解密的過程中，AES算法對語音數據信息進行加密以及解密所使用的輪密鑰均是通過初始的密鑰進行擴展得到的。因為這種擴展方式的存在，導致后續所生成的輪密鑰以及后續通過迭代生成的密鑰都與初始密鑰存在較強的關聯性。這種關聯性容易導致初始密鑰被逆向推出來，從而造成密鑰系統被破解的危險[9]。

通過查閱相關資料，并依據原始算法在對密鑰擴展中存在的不足，提出了AES算法的改進方案[10]。具體的改進方案為：首先通過對初始密鑰矩陣[W0,W1,W2,W3]進行行輸入、列輸出的置亂操作，然后生成狀態矩陣[A0,A1,A2,A3]；再對狀態矩陣與初始密鑰矩陣進行異或變化，得到后續生成子密鑰所必須的種子密鑰矩陣[W4,W5,W6,W7]；最后依據原始AES算法的密鑰擴展過程，以種子密鑰替代初始密鑰繼續完成生成子密鑰的操作，經過多次迭代后生成改進后算法所需要的所有的子密鑰。改進后的密鑰擴展過程如圖2所示。

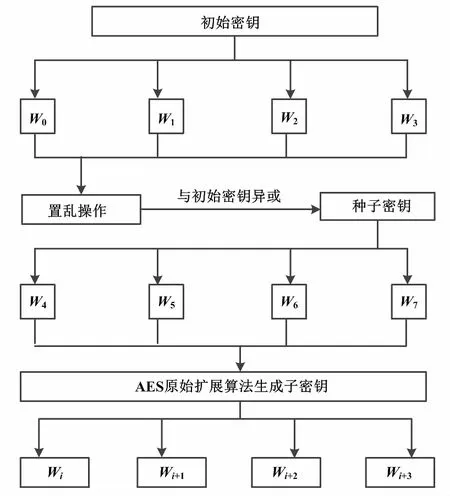
圖2 改進后的密鑰擴展過程圖

通過改進算法與原始算法在密鑰擴展的方式對比可知，改進后的算法通過對初始密鑰與輪密鑰進行列輸入與行輸出的置亂操作，可以有效降低初始密鑰和輪密鑰間的關聯性。其次，再將置亂后的兩個矩陣相異或變換。這個過程可以使得初始密鑰矩陣和種子密鑰矩陣之間只有對應的字之間有關聯。通過對兩個矩陣處理，進行異或變換可以防止出現破解的可能。最后，用得到的種子密鑰代替初始密鑰，經過密鑰擴展生成加解密過程所需要的全部子密鑰。通過分析發現，該優化方案不僅最大程度地繼承了原有密鑰擴展算法中的結構，而且加入的操作并沒有降低算法的執行效率。

在密鑰長度方面，密鑰長度是由種子密鑰[W4,W5,W6,W7]([W0,W1,W2,W3]與[A0,A1,A2,A3]的異或結果)決定的。因此對于破解者來說，想要利用子密鑰來推導出初始的密鑰，至少需要逆推232次；而想要破解整個密鑰系統，攻擊者至少要完成2128次窮舉[11]。由此可見，改進后的方案增強了原有算法的抗密碼分析能力。

在運行速度方面，由于改進的算法在原有的算法的基礎上加入異或變化，而對算法的執行效率會造成一定的影響。但是在實際的運算過程中，如果只是增加了兩個異或運算，在算法的整體運行速率上并不會產生太大的影響。同時，算法在處理信息的過程中，并沒有涉及很深的運算，因此在運行時間方面要遠小于子密鑰生成所需時間。另外，由于處理的語音數據在數據量和數據長度方面相對較大，算法本身并不需要進行頻繁的更換分組數據的初始密鑰，可以根據語音數據的傳輸周期進行適當的更換。因此，相對于原始算法在對密鑰擴展所使用的時間，改進后的算法在使用時間和運行效率方面都得到了很大的提升。

2 優化算法仿真分析

MATLAB是一種廣泛應用于數值分析、數據處理和算法開發的高級計算機語言。MATLAB平臺操作方便，同時擁有功能強大的工具箱和矩陣運算能力，在科學研究和工程設計領域都有普遍應用[12]。利用MATLAB對于數據處理的優勢，實現對改進后算法的可行性的仿真分析。

在進行MATLAB仿真中，可以使用平臺自帶的音頻讀入函數wavread()直接對輸入的語音樣本信息進行加密和解密操作。其偽代碼描述如下。

voice Path = [pathname filename];

[voice Origin,fs,bit] =wavread(voice Path);

//讀入一個語音文件

Is_voice Cip(i,:) = cipher (Is_voice Origin(:,i),w,s_box,poly_mat)

//語音加密

Is_voice Recover(i,:) = inv_cipher(Is_voice Cip(i,:),w,inv_s_box,inv_poly_mat,AESIndex);

//語音解密

改進算法對語音加解密的波形如圖3所示。改進算法對語音加解密的頻譜如圖4所示。

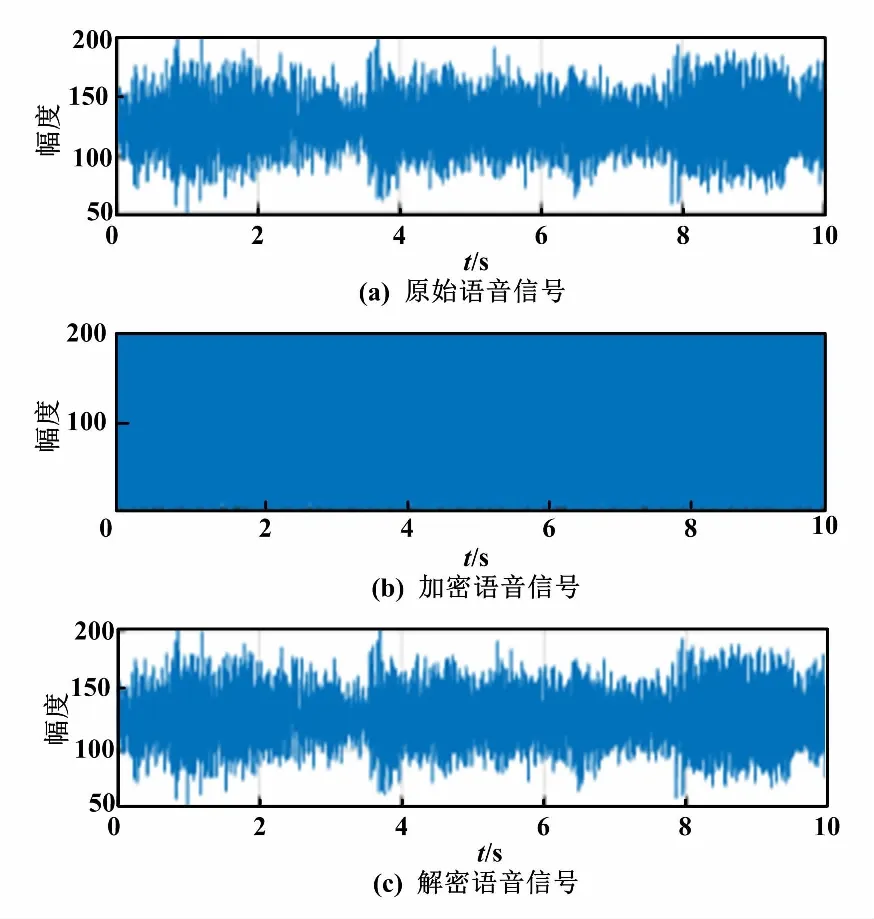
圖3 改進算法對語音加解密的波形圖

從圖3可以看出，原始語音采樣信號波形的波動變化較大，而經過改進算法加密后的語音信號被完全覆蓋了，因此很好地證明優化后的算法具備較好的混淆和擴散的特性。

從圖4可以看出，原始語音信號的頻譜幅度變化不是很均勻，但是通過AES算法加密后，獲得的密文信號的頻譜較為平坦。通過AES算法對加密的信息解密后得到的語音信號的頻譜與原始信號頻譜基本一致，幾乎保全了原始信號的全部數據量。因此可以得出，采用改進算法對語音數據加解密是可行的。改進算法在語音信號加解密過程中體現了較好的加解密特性。

3 優化算法STM32實現

為了進一步驗證改進AES算法的可實施性，將其移植到STM32硬件平臺上，對算法的性能和執行效率進行測試與分析[13]。在硬件平臺完成AES算法移植后，通過輸入語音信息并通過示波器對算法加密和解密效果進行驗證。

在計算機上選取一段可視的英文字符串作為明文數據，并將明文數據發送給STM32單片機。STM32將經過算法加密后的密文數據，通過串口通信上傳至計算機進行顯示。計算機得到的是一串雜亂無章的密文數據。根據計算機顯示的數據，需要加密的數據已經被STM32硬件平臺加密。此時，再將加密的數據下發至主控芯片進行解密處理，通過硬件平臺解密處理后的數據與原始數據對比發現，數據保持一致。根據試驗現象分析發現，AES算法在STM32硬件平臺上可以實現對字符串進行加解密的操作。通過后續對不同長度字符的硬件加解密測試，對測試數據進行對比分析發現，明文數據進行加密和解密處理后的數據與原始數據基本保持一致，驗證了AES算法的穩定性和可靠性。

4 結論

針對原有AES算法在密鑰擴展過程存在密鑰之間關聯性強的問題，提出了一種優化方案，通過對初始密鑰進行置亂和異或操作，降低了初始密鑰與輪密鑰之間的關聯性，可以在原算法的基礎上提高抗密碼攻擊能力。在對AES算法理論進行簡要闡述后，分析現代傳統AES算法存在的缺陷并作出算法的改進，在原有算法基礎上有效提高算法的安全性和運行效率。同時，通過MATLAB平臺對改進后的算法進行仿真。結果表明，改進后的算法提高了可靠性和安全性；通過在STM32硬件平臺上的實現，進一步驗證了優化算法的高效性和可實施性。