面向數據驅動的城市軌道交通短時客流預測模型

梁強升，許心越，劉利強

（1.廣州地鐵集團有限公司 運營事業總部，廣東 廣州 510330；2.北京交通大學 軌道交通控制與安全國家重點實驗室，北京 100044）

1 引 言

城市軌道交通以其運量大、速度快、可靠性高等運行特點，已成為人口密集大城市的首選交通方式［1］。我國城市軌道交通建設快速增長，誘發了客流的急劇上升［2］，導致軌道交通擁擠、服務質量下降。因此，如何分析管理城市軌道交通客流，特別是把握客流的短時變化規律已成為運營管理者提高城市軌道交通運行效率、緩解擁堵、提高服務質量迫切需要解決的問題［3］。

城市軌道交通客流短時預測方法主要分為經典的統計模型和機器學習模型。經典的統計模型主要包括自回歸綜合移動平均（ARIMA）和指數平滑模型，在早期得到了廣泛的應用［4］。例如，NI等［5］將線性回歸和ARIMA 模型相結合對紐約地鐵的短期客流進行了預測。WILLIAMS 等［6］基于季節ARIMA 模型預測交通流量。然而，這些統計方法大多屬于線性的時間序列模型，無法捕捉客流的非線性變化，導致其進行短時客流預測的誤差較大［7］。

為解決這一非線性預測難題，機器學習方法應運而生。機器學習方法包括支持向量機、貝葉斯網絡、k-鄰近算法、人工神經網絡等。例如，SUN等［8］提出了一種小波-支持向量機混合方法對北京地鐵系統的換乘客流進行預測。ROOS 等［9］提出了一種利用不完整歷史觀測數據預測短期客流的動態貝葉斯網絡方法。JIAO等［10］提出了一種基于貝葉斯組合和非參數回歸的改進卡爾曼濾波模型來預測北京地鐵13 號線高峰時段的客流。WEI 等［11］將經驗分解模式與前饋神經網絡相結合對短期客流進行預測，結果表明該模型的預測精度優于ARI?MA 模型。LI 等［12］提出用徑向基函數神經網絡預測單站客流。然而，所有這些模型都基于淺層結構，無法捕獲數據中的復雜非線性關系［13-14］。

近年來，循環神經網絡、長短期記憶神經網絡、門控遞歸單元神經網絡和卷積神經網絡由于在捕捉時空關系方面具有優越的性能而受到廣泛重視［15-17］。在時間預測方面，循環神經網絡利用輸入序列和時間步長之間的連續反饋來獲得時間相關性；而長短期記憶神經網絡和門控遞歸單元神經網絡，可以處理比循環神經網絡更長的序列［18］。同時，長短期記憶神經網絡和門控遞歸單元神經網絡都可以借助門控機制解決循環神經網絡中的梯度消失和梯度爆炸問題［17］。在空間預測方面，由于卷積神經網絡的參數共享機制和連接稀疏性，使得卷積神經網絡具有很好的空間信息特征。因此，結合長短期記憶神經網絡、門控遞歸單元神經網絡和卷積神經網絡進行客流預測時，可以綜合考慮客流的時空特征。例如，DU 等［19］提出一種深度不規則卷積殘差長短期記憶神經網絡對城市交通客流進行預測。DO 等［20］應用卷積神經網絡和門控遞歸神經網絡預測流量，該模型可以有效地提取動態時空特征。然而，這些既有的模型僅適用于單條線路的客流預測，無法考慮路網間的客流特征，難以實現對路網的客流預測。

近年來，一種擅長解決這類網絡空間相關性問題的圖卷積神經網絡方法被提出，并得到了廣泛關注。YU 等人［21］采用圖卷積神經網絡提取路網的空間相關性，從而對交通速度進行預測。雖然圖卷積神經網絡被證明具有較強的預測精度和可解釋性，但如何結合城市軌道交通自動售檢票系統（AFC）和時刻表數據利用圖卷積神經網絡方法進行短時客流預測的研究尚屬空白。

綜上，本文提出了一種新的融合循環門控單元的時空圖卷積神經網絡（GCGRU）模型來預測城市軌道交通的短時客流。本方法提出使用圖卷積神經網絡來描述短時客流的空間特征，特別是提出了基于旅行時間的鄰接矩陣構建方法，并進一步融合循環門控單元描述客流間的時間特征，形成了考慮客流時空演化關系的城市軌道交通短時客流預測模型，具有較強的預測精度和可解釋性。

2 數據驅動的短時客流預測方法

2.1 問題描述

設城市軌道交通網絡用1 個加權有向圖G=(V，E)表示：V為城市軌道交通車站集合，E為線路區間集合。設鄰接矩陣為A，矩陣中各個元素的值代表每2 個站點間的旅行時間；設站點特征矩陣為X：其中X的行數N為站點數量，列數P為車站的特征屬性（即時間步長）。歷史進站量為每個車站的特征屬性，xi是每個站點在第i個時間步長的進站量。

不同車站類型（樞紐、通勤、商業等）和土地性質差異會產生不同的客流導向，導致不同站點在不同時段有不同的客流特征。土地性質及站點類型等因素造成進出站量的變化，并可通過進站量來反映這些變化，因此進站量常被作為主要輸入變量進行出站量的預測。

某一車站的客流經過列車運輸分散到路網各個相關車站，不同車站的客流經過特定列車運輸到達同一個目的車站，因此車站的進站客流會影響到其他車站的出站客流。本文根據城市軌道交通路網中各站點的歷史進站量來預測未來的出站量。因此，城市軌道交通短時客流預測問題可轉化為根據鄰接矩陣A和節點的進站客流量特征矩陣X來學習映射函數f，即

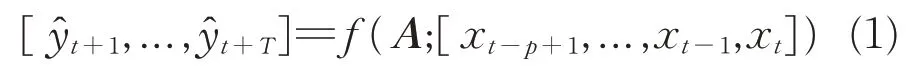
2.2 面向數據驅動的短時客流預測模型

本節提出面向數據驅動的短時客流預測方法分為2 部分：①用來提取序列空間特征的圖卷積神經網 絡GCN （Graph Convolutional Networks）神經網絡；②用來提取時間特征的門控遞歸單元神經網絡GRU（Gate Recurrent Unit）神經網絡。第1 部分的輸出作為第2 部分GRU 的輸入。具體模型框架如圖1所示。

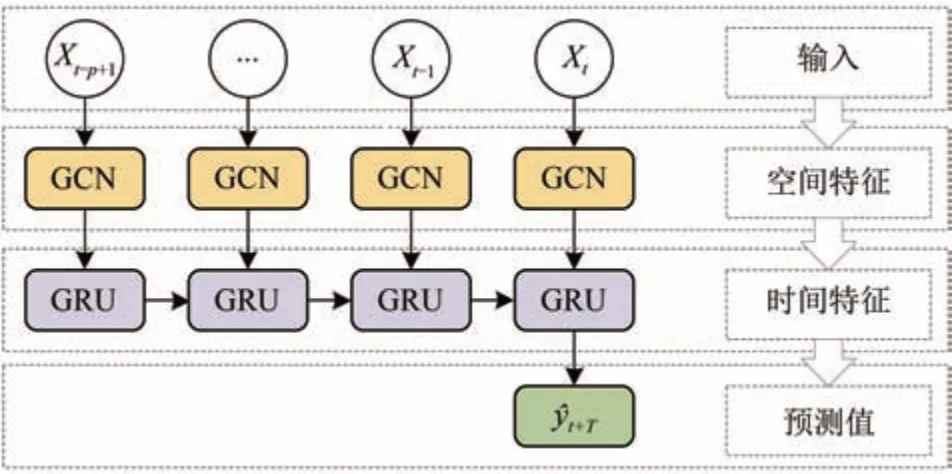
圖1 模型框架

2.2.1 空間圖卷積網絡模型

圖中G=(V，E)具有2 種特征：節點特征和結構特征（節點之間的依賴關系）。GCN 神經網絡有2 種：一種基于頂點域或空間域，另一種基于頻域或譜域。本文采用基于空間域的GCN 來學習圖的結構特征。

GCN 模型有2 個輸入：鄰接矩陣A和進站客流特征矩陣X。鄰接矩陣A的表達式為

式中：tij為乘客從車站i到車站j的平均旅行時間。

GCN 的層與層之間的傳播方式可表示為

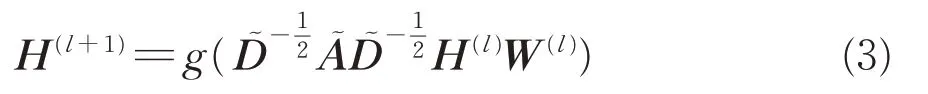
式中：H(l)，H(l+1)分別為第l層和第(l+1)層的特征矩陣；g為斜坡激活函數；為鄰接矩陣與單位矩陣的和，=A+I；為的度矩陣；W(l)為第l層的權矩陣。初始層H(0)的特征矩陣為進站客流量特征矩陣X，且g和可由下面公式計算

由于GCN 層的最佳數量是2～3，本文選取2層GCN模型，故可將式（3）重新表述為

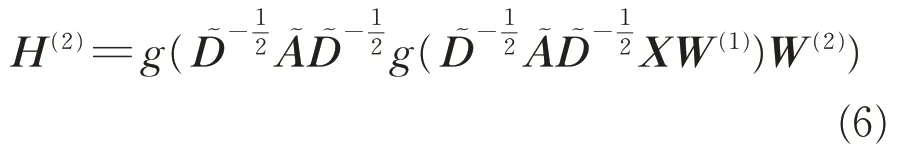
2.2.2 GRU模型

GRU用以捕捉預測數據間的時間信息，它有2個門：更新門（表示為zt）和重置門（表示為rt），如圖2所示。更新門決定了客流預測保留多少以前的狀態，重置門決定了新輸入與前一狀態融合的程度。更新門的值越大，則前一個時間步長內的信息被帶入的就越多。重置門的值越小，則前一時間步長內的信息越容易被忽略。

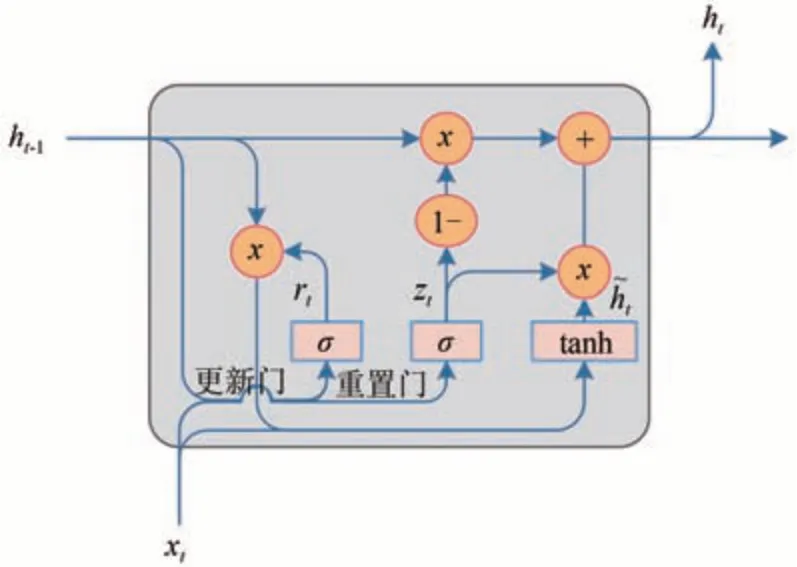
圖2 GRU的計算圖

GRU的輸入用矩陣X′=[x′t-P+1，x′t-p+2，...，x′t]表示，是H(2)（GCN模型的輸出）的轉置矩陣。

每個GRU的狀態計算如下。

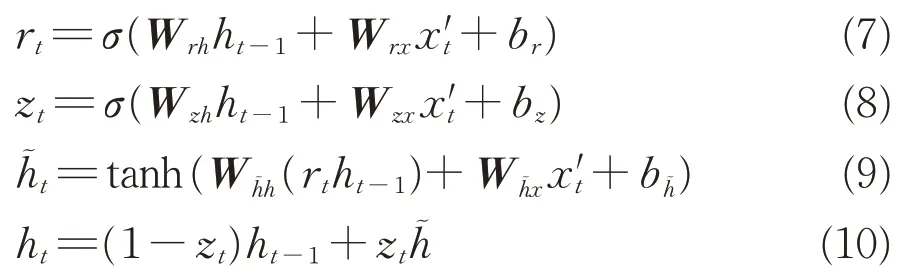
式中：Wrh，Wrx，Wzh，Wzx，Whh，Whx為加權矩陣，控制著隱藏層到相應的輸入的連接；ht-1為第t-1個時間步長的隱藏狀態；br，bz，為偏置項；為當前記憶內容；ht是第t個時間步長的隱藏狀態，也是GRU 的輸出；σ是sigmoid 函數，σ和tanh 是由以下公式定義的非線性激活函數。

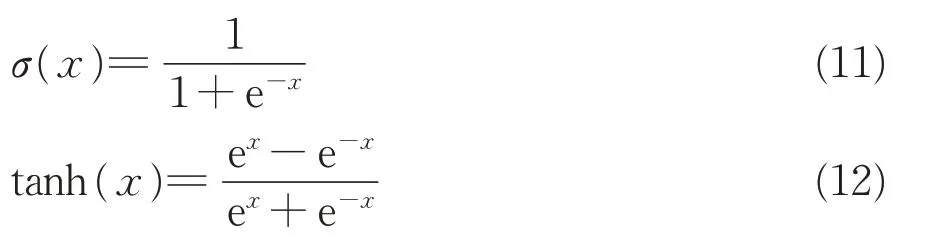
2.2.3 損失函數

在模型訓練過程中，目標是城市軌道交通網絡實際客流量與預測值之間的誤差最小化，即模型的損失函數為

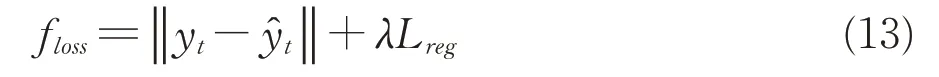
本文提出的模型具有以下優點：

（1）可以通過鄰接矩陣學習城市軌道交通網絡系統中各站點之間的空間相關性，解決了傳統CNN 模型不能預測網絡層次客流的問題。目前應用于道路網絡層次的GCN 都是基于地理距離來構建鄰接矩陣，而本文基于旅行時間來構建鄰接矩陣，能更準確地學習各站點之間的空間關系。

（2）采用的GRU 模型通過更新門和重置門對歷史客流信息進行篩選，以解決序列之間的依賴關系，實現對較長時間序列的精準預測。此外，GRU 中的2 個門控單元均采用了非線性函數，能夠有效識別客流中的復雜非線性關系。

（3）本模型結合GCN和GRU模型可以實現城市軌道交通全網的時空客流預測，與傳統只考慮時間關系的模型相比，本模型的預測精度更高、解釋性更強。此外，本模型采用數據驅動的方法來學習城市軌道交通網絡中的時空關系，具有較強的穩定性和魯棒性。

3 預測模型及分析

3.1 數據描述

選取廣州地鐵6 個重要的就業型站點為例，對客流預測模型進行有效性驗證。所選取的車站具有客流量較大或是重要的換乘站等特點，即：客村、楊箕、珠江新城、體育西路、公園前、琶洲，如圖3所示。預測數據采用2017年5月15日至5月27日的廣州地鐵路網數據、AFC 數據（見表1）和時刻表數據，這些數據含周末的客流量。基于以上數據構建預測模型相關的2個矩陣。

（1）描述城市軌道交通車站間空間關系的6×6鄰接矩陣。矩陣的行表示車站，矩陣中的值為乘客在站與站之間的平均旅行時間，可由時刻表數據確定。

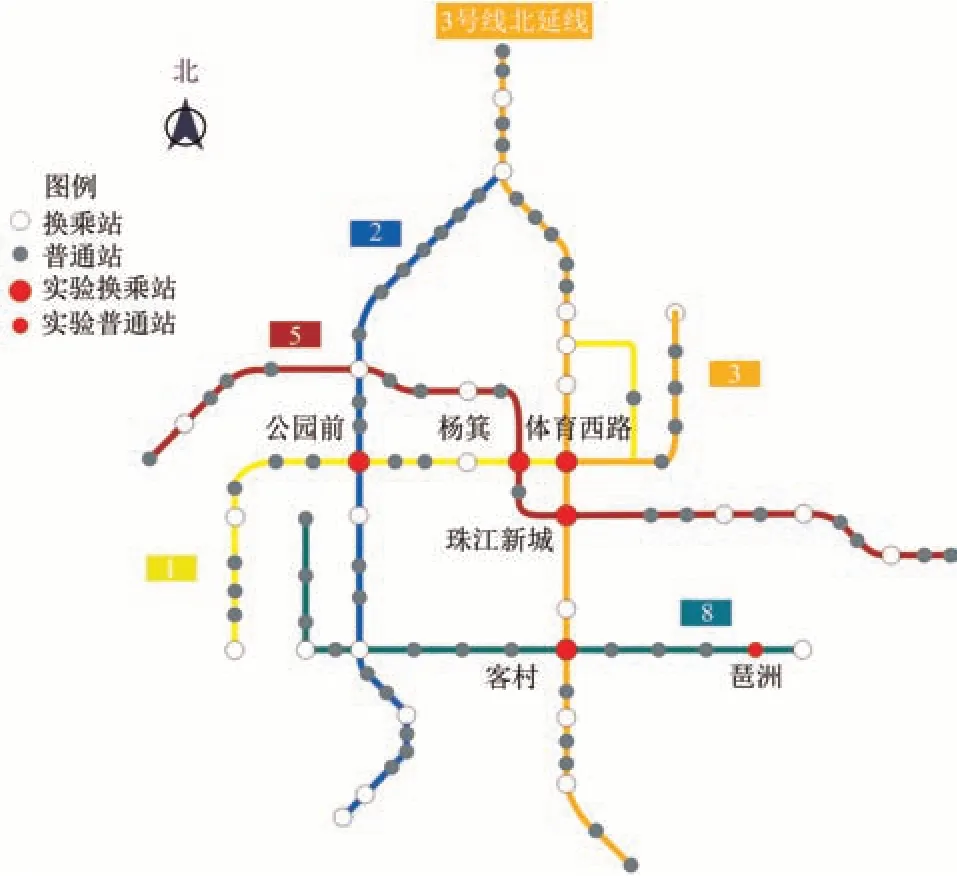
圖3 典型的廣州地鐵車站示意圖

（2）描述每個車站進站和出站客流隨時間變化的特征矩陣和標簽矩陣。矩陣的行表示一個時間步長內各站點的客流量，列表示在不同時間段內各站點的客流量。其中：客流量是根據AFC 數據進行15 min粒度統計后的量。進一步利用最小-最大規范化技術，將矩陣內的數值規范化到［0，1］范圍內。

表1 AFC數據樣本

3.2 評價指標

選取均方根誤差（SRMSE）、平均絕對誤差（SMAE）、精度（SACC）、決定系數（R2）和可釋方差得分（SVar）5 個評價指標來評價模型的性能，它們的計算公式如下。

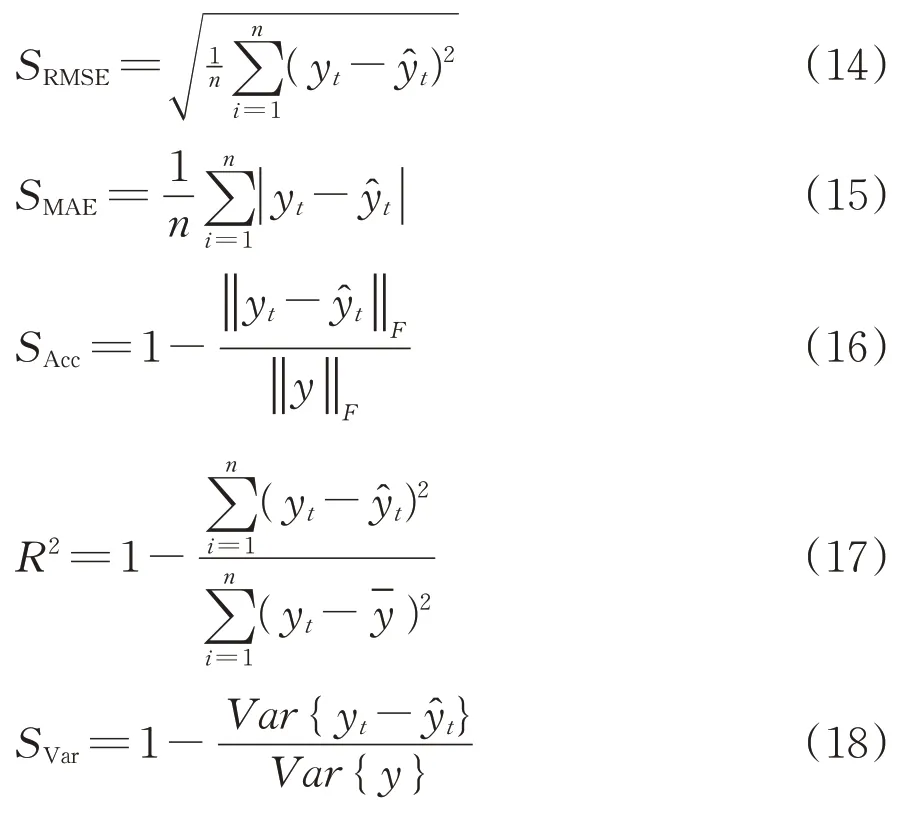
在上述評價指標中，SRMSE和SMAE都是用來度量預測誤差的，兩者都是絕對指標，且值越小，預測性能越好。SACC，R2和SVar都是相對指標，值越大，預測性能越好。

3.3 參數調整

GCGRU 模型的超參數主要包括學習率、批大小、訓練次數、隱藏單元數和正則化參數。在本次實驗中，學習率初始值設為0.001，并用Adam 優化器自動優化；批量大小一般設置成2 的n次方，批量大小越大，模型精度越低、訓練速度越快，通過手動調節并綜合考慮精度和訓練速度，最終將其設為64；當訓練次數達到2 000 時，模型的精度不再上升，因此將訓練次數設為2 000；將λ分別設定為0，0.1，0.01，0.001，0.001 5，0.002，當λ為0.001 5 時，模型精度達到最高，因此將λ設置為0.001 5。以上參數對模型5 個評價指標的影響都很小，因此不再進一步分析。

由于隱藏單元數對深度學習模型的5 個評價指標有很大的影響［14］，因此本文對不同數量隱藏單元下的GCGRU 模型進行了實驗（分別設定8，16，24，32），以獲取最優的隱藏單元數。實驗結果如圖4所示。隨著隱藏單元數的增加，SRMSE和SMAE先減少后增加，SACC，R2和SVar的值呈現相反的變化趨勢。當隱藏單元數為24 時，SRMSE和SMAE達到最小，SACC，R2和SVar的值同時達到了最大。因此，最優的隱藏單元數為24。

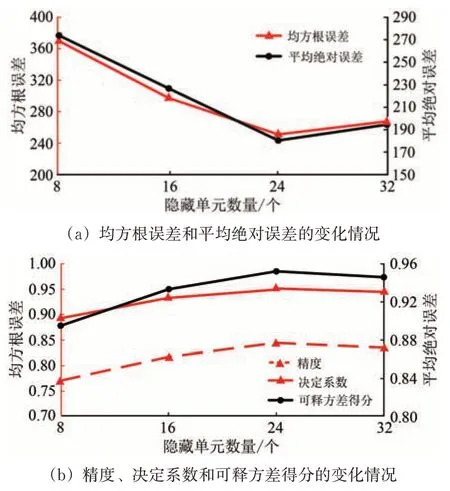
圖4 不同隱藏單元數下評價指標的變化

3.4 模型評價

選取以下模型作為基線模型進行對比分析。

（1）ARIMA 模型是典型的時間序列模型，擅于處理時間序列數據。該模型有3個整數型的參數p，d，q，該模型通過自動遍歷不同的p，d，q組合，確定最優組合為：p=1，d=1，q=1。

（2）支持向量機（SVR）：SVR 是經典的機器學習模型，它利用歷史數據對模型進行訓練，得到輸入和輸出之間的關系，因此常用于預測客流。選取帶有線性核的SVR模型作為比較模型。

（3）前饋神經網絡（BP）： BP 模型是基本的神經網絡模型，能夠處理非線性關系。BP 模型有學習率（自動調節）、批量大小、訓練次數、正則化系數λ以及隱藏單元數5 個參數，其調節過程與3.3節所敘方法一樣。調參結果為：批量大小為64，訓練次數為2 000，λ為0.001 5，隱藏單元數為24。

（4）GRU：GRU 是深度學習模型，具有捕捉時間信息的能力。GRU 的參數與BP模型一樣，調節結果為：批量大小為64，訓練次數為2 000，λ為0.001 5，隱藏單元數為24。

本文在不同預測步長下利用以上各種模型進行了客流預測，結果見表2。

3.4.1 整體預測結果

首先，將本文提出的GCGRU 模型與其余4 個模型（ARIMA，SVR，BP 和GRU 模型）的SRMSE進行了比較，不同模型的SRMSE比較結果如圖5所示。對于15 min 的預測步長，GCGRU 的SRMSE分別比ARIMA，SVR，BP和GRU 模型的SRMSE降低了80.5%，77.4%，33.7%和28.9%。因此，本文提出的GCGRU 比4 個對比模型的預測誤差都低。

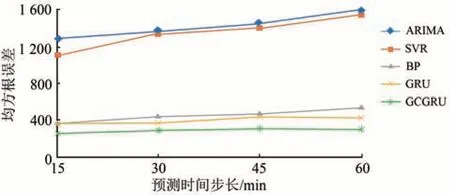
圖5 5個模型的均方根誤差比較結果

其次，將GCGRU 模型與不具備時間信息捕捉能力的非線性模型（SVR 和BP 模型）進行了比較分析。從表2中可以看出，SVR 模型的SACC太小以至于可被忽略，因此，只將GCGRU 模型的精度SACC與BP 模型和GRU 模型進行對比，如圖6所示。對于15 min 的預測步長，GCGRU 模型的SACC分別比BP 模型和GRU 模型的SACC提高了10.4%和8.1%。因此，本文提出的GCGRU 模型比SVR模型和BP模型的預測精度都高。

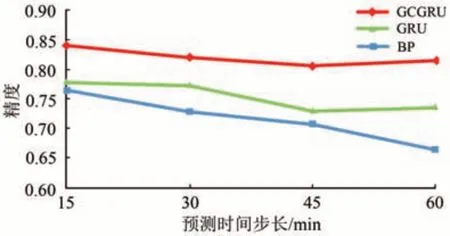
圖6 模型精度比較

最后，將GCGRU 模型與不具備空間信息捕捉能力的GRU模型進行了對比，結果如圖7和圖8所示。對于15，30，45 和60 min 的預測時間步長，GCGRU 模型的SRMSE比GRU 模型分別降低了28.9%，21.4%，29.8%和29.8%，SACC分別提高了8.1%，6.3%，10.9% 和10.6%。因此，GRU 和GCN 融合模型實現了數據中時空關系的高效挖掘，預測效果比既有的GRU模型好。

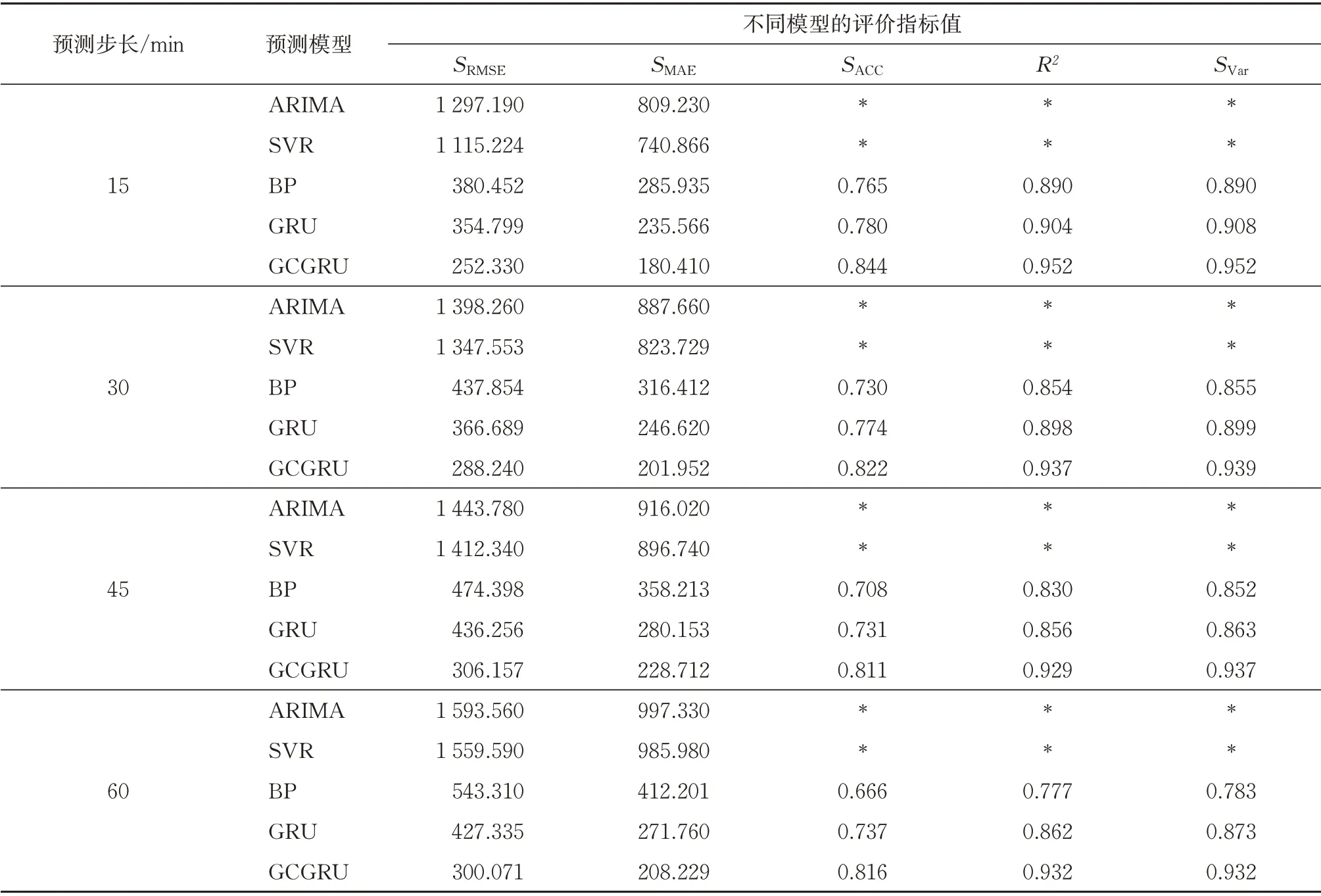
表2 GCGRU模型和基線模型預測性能的比較結果

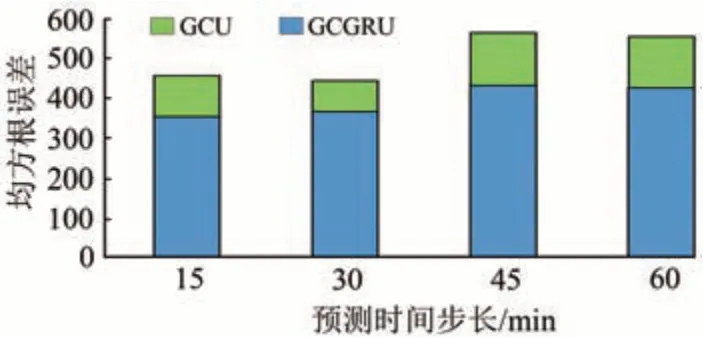
圖7 GCGRU模型與GRU模型的均方根誤差比較

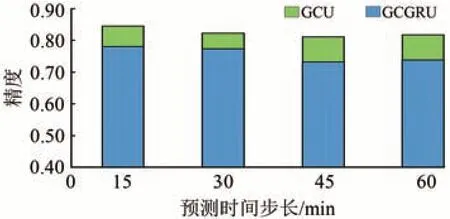
圖8 GCGRU模型與GRU模型的預測精度比較

綜上，與所有基線模型相比，本文提出的GCGRU模型在不同的評價指標和預測時間步長情況下的表現性能都最好。

3.4.2 單個車站預測性能

將GCGRU 模型與GRU 模型在每個車站的預測性能進行了進一步的比較分析，得到圖9和圖10。由圖可知，對于每個車站而言，GCGRU 模型的SRMSE比GRU 模型的都低，R2GRU 模型的也高；特別在公園前車站，GCGRU 模型與GRU 模型的SRMSE差距最大，前者相對于后者降低了47.8%；在體育西路車站，GCGRU 模型與GRU 模型的R2差距最大，前者相對于后者提升了23.9%。此外，GCGRU 模型預測結果中琶洲站的SRMSE最高，R2最低。這主要是因為琶洲車站附近有展覽中心，經常會有展覽活動，因此預測效果不是很好，未來需要進一步挖掘時空關系和外在因素。

圖9 GCGRU模型和GRU模型在不同車站的均方根誤差比較

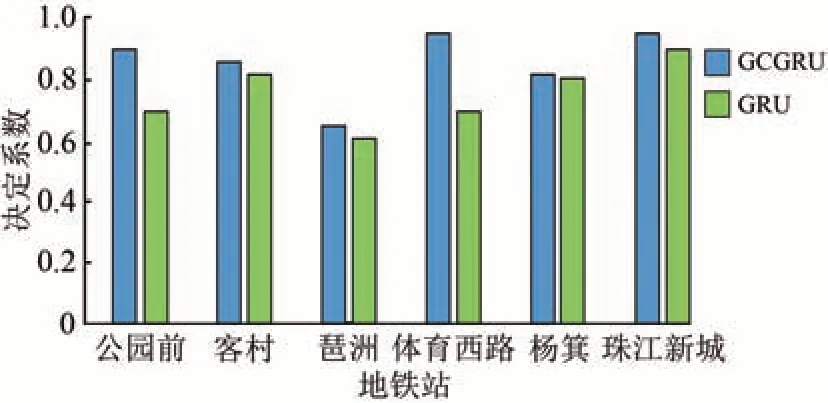
圖10 GCGRU模型和GRU模型不同車站決定系數比較

圖11為6 個車站的2017年5月客流擬合圖。由圖可知：琶洲站和珠江新城站的客流呈單峰趨勢，且都為早高峰；其余車站都呈現早晚雙峰趨勢。進一步分析，在琶洲站，GRU 模型在高峰時期的預測值比真實值低，如圖11（c）所示；而在楊箕站，GRU 模型在高峰時期的預測值又比真實值高，如圖11（e）所示。因此，GCGRU 模型的預測效果優于GRU模型。

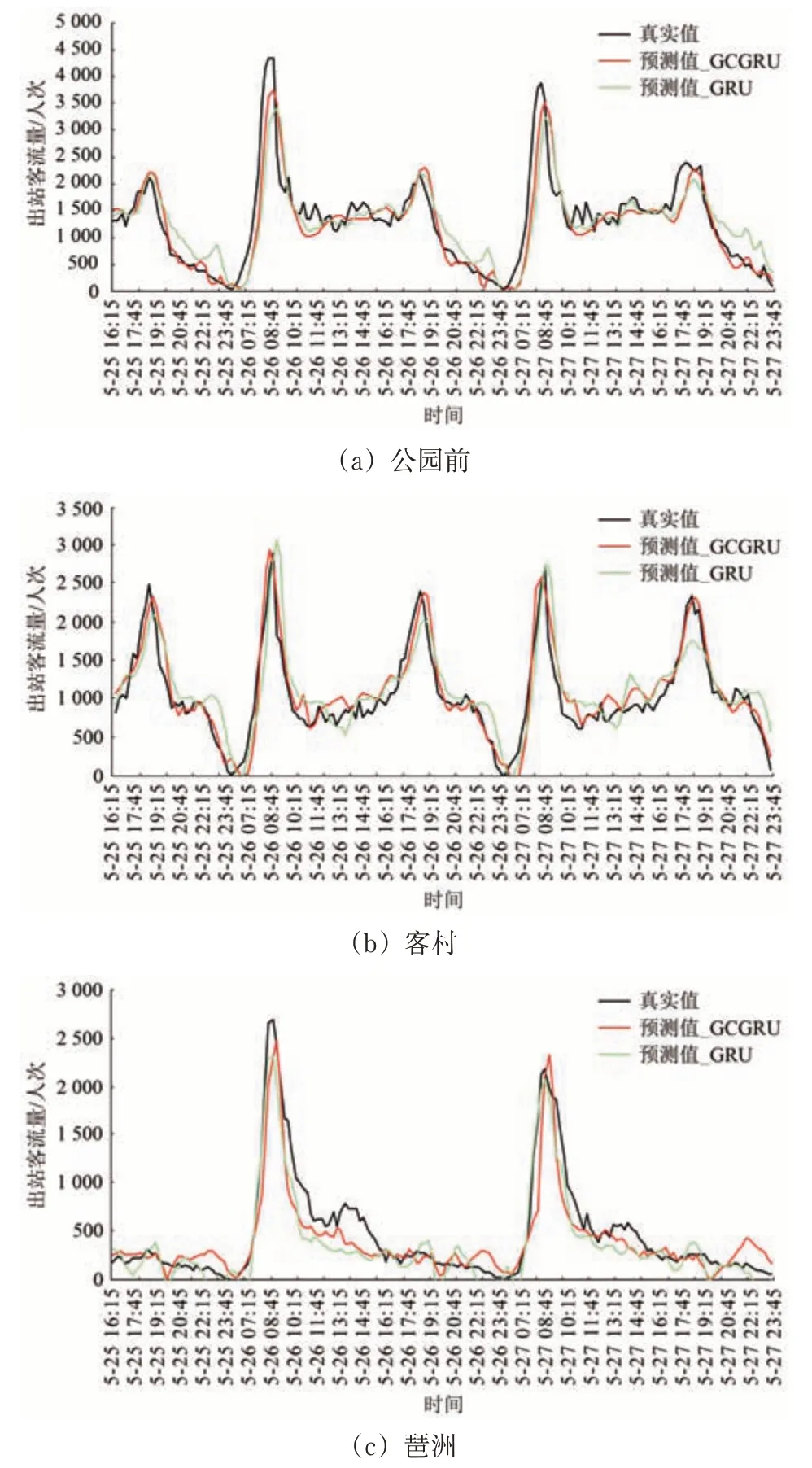
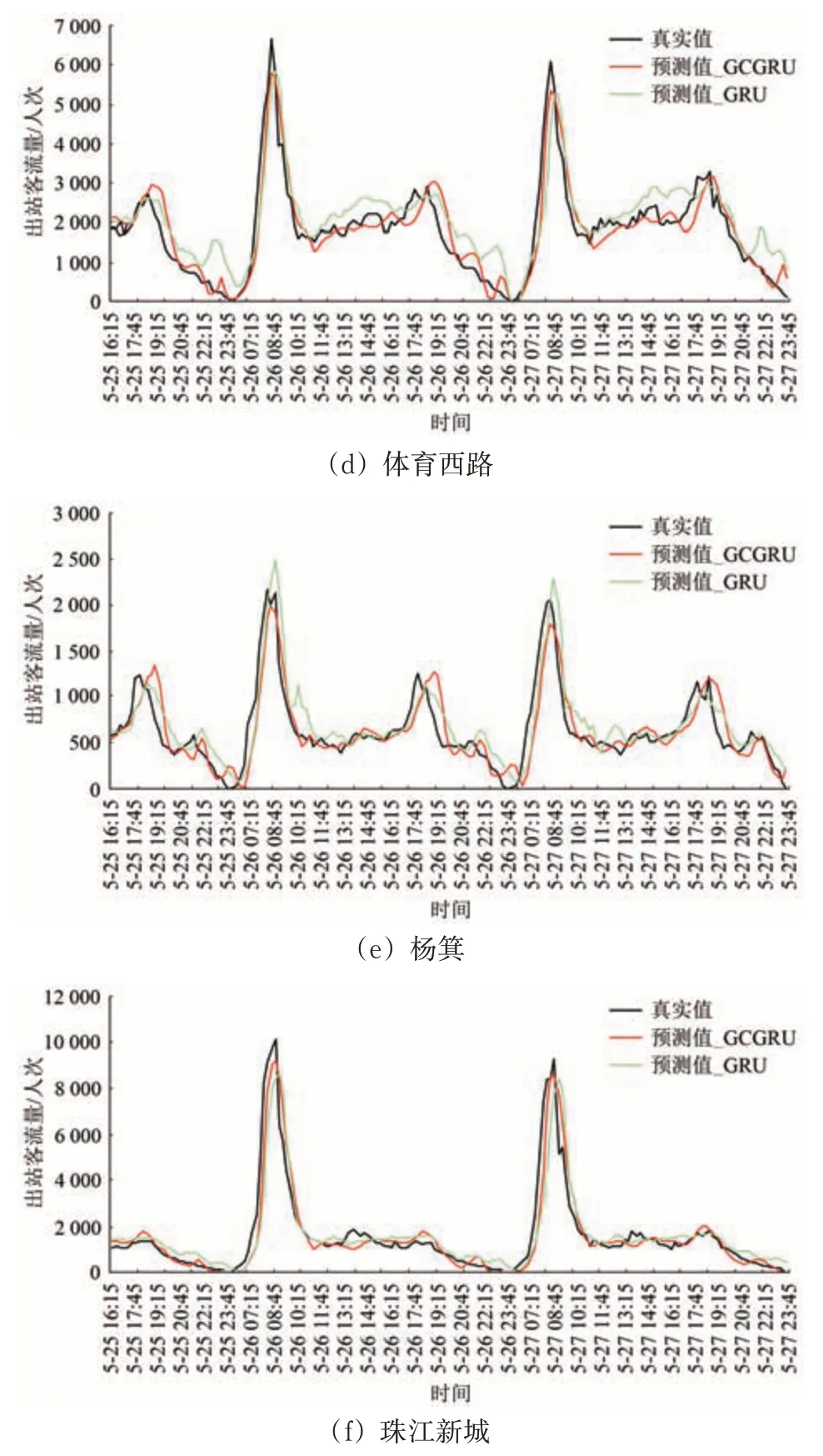
圖11 不同車站的客流擬合曲線圖

3.4.3 鄰接矩陣影響

為了驗證旅行時間鄰接矩陣的有效性，將GC?GRU 模型與地理鄰接矩陣的模型進行了比較。令基于地理鄰接矩陣的模型為GCGRU*，比較GC?GRU 與GCGRU*在不同預測步長下的SRMSE與SACC，如圖12所示。針對15，30，45 和60 min 的預測步長，GCGRU 比GCGRU*的SRMSE分別減少了6.1%，2.7%，2.4%和5.3%；SACC分別增加了0.8%，1.0%，1.0% 和3.0%。由此可見，GCGRU 的預測性能更好，因此基于旅行時間構建的鄰接矩陣更適合于城市軌道交通網絡的短期客流預測。

4 結 語

圖12 GCGRU與GCGRU*預測的均方根誤差和精度比較

本文提出了1 種新的融合循環門控單元的時空圖卷積神經網絡模型（GCGRU）來預測城市軌道交通短時客流。循環門控單元用以提取時間特征，圖卷積神經網絡用以提取空間特征。以廣州地鐵路網6 個車站的短時客流預測為例進行模型的有效性驗證。結果表明，該模型的預測性能優于ARI?MA，SVR，BP 和GRU 等基線模型，對于整體預測結果來說，精度至少提高了6.3%，最多可提高80.5%。對于單站客流預測結果來說，精度至少提高了1.4%，最多可提高23.9%。因此，本文提出的模型能夠有效地刻畫各車站客流間的時空演化關系，具有精度高、解釋性強等特點，可以較好地為城市軌道交通日常客流組織和管理提供輔助決策。

本文提出的模型是1 個靜態的空間卷積網絡模型，其鄰接矩陣不會隨著時間而改變。但實際上，各站點之間的空間關系會隨時間變化。因此未來可嘗試將動態的GCN與GRU相結合來預測客流。本文提出的模型目前只考慮了鄰接矩陣和進站客流對出站客流的影響。實際上，出站客流還受到周期、時段以及天氣等因素的影響，未來可將這些因素考慮到模型中，以提高模型精度。此外，未來本模型還可以考慮應用在進站量預測上。