基于時間序列ARIMA模型的高職高專院校生師比預測

于明星

(朝陽師范高等專科學校 信息工程系，遼寧朝陽122000)

0 引言

隨著我國經濟的迅速發展，高職高專階段的生源數量顯著提高，高校的招生數量也隨之升高.高職高專教育已由穩定發展期過渡到新探索時期，學生數量的持續增加和畢業生質量的下滑受到社會的普遍關注.為了實現教育大眾化、現代化、公平化，教育部頒布了系列文件[1],其中2004年印發的《普通高等學校基本辦學條件指標》中就招生規模及招生條件等多項指標作出了規定，明確指出在校生人數與專任教師比率不應超過18∶1.生師比是反映高職高專院校辦學質量的一項重要指標[2]，是高等教育大眾化進程中質量建設的基礎，是一流大學守望精英教育質量的傳統，是高等教育大眾化進程中大學質量改革的理性判斷[3].高職高專院校在積極擴招的態勢下，在校生數量急速增長，但專任教師數量增幅卻跟不上節奏，嚴重影響了高職高專教育的教學質量.通常生師比比值與教學質量具有反比關系，文獻[4]通過分析2003～2013年間全國普通高校生師比的數據發現，國家重點建設大學及985工程大學的生師比較低，并針對高校生師比現狀，提出了一些改善生師比的對策.文獻[5]利用遺傳算法優化的BP神經網絡模型對未來幾年普通高校的生師比進行了預測.文獻[6]利用數據平臺建立了高職院校生師比狀態函數，進而通過數據函數值來分析院校的辦學質量及辦學規模等.

目前，已有較多研究關注生師比這一指標，大多集中于本科院校的現狀及對策上的分析，而對高職高專院校生師比指標的預測研究相對不足，這影響著我國高職高專教育的招生及可持續性的健康發展.本研究中通過分析教育部高職高專院校的生師比數據，結合自相關系數表和偏自相關系數表來判斷初始數據的平穩性，分析出自回歸分量階數p和移動平均分量階數q，進而確定相應的ARIMA(p,d,q)模型，通過該模型來預測未來幾年高職高專院校生師比指標.

1 ARIMA數學模型

ARIMA(全稱Auto Regressive Integrated Moving Average)模型，即自回歸移動平均模型，由Box-Jenkins于20世紀70年代提出的是一種時間序列分析法[7]，其基本思路是對初始數據進行時間上的階數平移而形成一個隨機序列，用以描述這個隨機序列的屬性模型就是ARIMA模型.該模型可以利用時間序列的過去值去分析未來值，在預測農產品價格[8]、交通事故[9]、網絡流量[10]和電氣負荷[11]等多方面具有廣泛的應用.ARIMA模型中有三個參量，分別為自回歸分量階數p、差分次數d和移動平均分量階數q，通常用ARIMA(p,d,q)表示[7].

結合高職高專院校不同研究數據的特點，構建最優的ARIMA預測模型.定義研究數據觀測值zt滿足

zt=λ1zt-1+λ2zt-2+λ3zt-3+…+λpzt-p+vt

(1)

式中：λt—— 回歸參數，其中i=1，2，…，p為滯后變量數；vt—— 白噪聲過程.則線性數據觀測值zt就是p階自回歸模型，表示為AR(p).

白噪聲vt用滯后算子表示為

vt=Λ(L)zt=(1-λ1L-λ2L2-…-λpLp)zt

(2)

式中：Λ(L) —— 自回歸算子.

自回歸算子變式為

(3)

當特征方程滿足Λ(L)=0時，AR模型在p階平穩.

若研究數據觀測值zt滿足

zt=vt+θ1vt-1+θ2vt-2+θ3vt-3+…+θqvt-q

(4)

式中：θ1,θ2,…，θq—— 參數；vt-q——t-q時所對應的白噪聲.研究數據觀測值zt就是q階移動平均模型，表示為MA(q).

式(3)變形為

zt=Θ(L)vt=(1+θ1L+θ2L2+…+θqLq)vt

(5)

式中：Θ(L)——移動平均算子.

移動平均算子特征方程為

Θ(L)=1+θ1L+θ2L2+…+θqLq=0

(6)

移動平均算子變式為

(7)

那么,研究數據觀測值

(8)

式中：k1,k2,…，kq——常數.

當特征方程滿足Θ(L)=0，MA模型在q階可逆.

ARMA模型由AR模型和MA模型組合構成，表達式為

zt=λ1zt-1+λ2zt-2+λ3zt-3+…+λpzt-p+vt+θ1vt-1+θ2vt-2+θ3vt-3+…+θqvt-q

(9)

綜合式(2)和式(5)，ARMA模型可變形為

Λ(L)zt=Θ(L)vt

(10)

若時間序列不具有平穩性，則需要對不平穩模型進行差分處理，那么此ARMA模型就是ARIMA模型.

為了分析數據的變化率情況，引入增比指標，其表達式為

(11)

式中：zi——第i年的數據；zi-1——第i-1年的數據.

其基本過程為：

(1)根據初始高職高專院校教育統計數據的自相關系數表和偏自相關系數表判定序列的平穩性，通常初始的數據為不平穩的時間序列.

自相關系數計算公式為

(12)

偏自相關系數計算公式為

(13)

(2)若初始的統計數據為非平穩的時間序列，且具有一定的變化趨勢，則對該組數據進行一階差分處理，如果一階差分后的數據依然為非平穩的時間序列，則進行二階差分處理，一般差分次數控制在2次之內.

(3)根據時間序列模型判定規則[7]，建立合理的時間序列模型.若偏自相關系數呈截尾性，自相關系數呈拖尾性，則移動平均分量階數為0，自回歸分量階數為p；若偏自相關系數呈拖尾性，自相關系數呈截尾性，則移動平均分量階數為q，自回歸分量階數為0；若偏自相關系數呈截尾性，自相關系數呈截尾性，則移動平均分量階數為p，自回歸分量階數為q.

(4)利用步驟(3)確定的ARIMA(p,d,q)分析初始數據，得出預測結果.

ARIMA模型能夠依據變量自身的變化規律，利用外推機制判斷出研究對象的變化情況,通過處理預測目標的時間序列，獲得事物隨時間變化的演變特性及規律，從而預測事物未來的發展方向.ARIMA模型的基本適用條件是要求預測的數據滿足平穩性特征，即個體值要圍繞均值小幅波動，存在某些周期規律特性，且不存在明顯的變化趨勢(若出現明顯變化趨勢，則需要對預測數據進行差分處理).高職高專院校的在校生數量和專任教師數量隨著年份的增加而不斷變化，雖然在每個季節的數量都不盡一致，但卻存在某種規律性，每一年周期內在校生數量和專任教師數量的波動趨勢大致相似，具有連續性和周期性，故適用ARIMA模型進行預測.

2 高職高專院校現狀分析

表1為高等教育院校規模變化表，數據來源于教育部網站公布的2009～2017年全國教育事業發展統計公報[12～20].由表1可知：高職高專院校數量比本科院校要多；本科院校數量從2009年開始逐年上升，高職高專院校數量從2009～2017年也穩步提升；2012年以前高職高專院校的增長幅度較大，2012年以后其增長幅度落后于本科院校，但自2017年開始，增長幅度再次超過本科院校.

表2為高等教育專任教師數量變化表，數據來源于教育部網站公布的2010～2017年全國教育事業發展統計公報[13～20].由表2可以發現:本科院校專任教師數量比高職高專院校專任教師數量多;本科院校專任教師數量從2010年開始逐年上升，高職高專院校數量從2010～2017年也穩步提升;2015年以前本科院校專任教師增比要大于高職高專院校，自2015年開始，高職高專院校專任教師增比幅度大于本科院校;就總體趨勢來看，本科院校專任教師增比處于下滑趨勢，高職高專院校專任教師增比處于穩步上升趨勢.

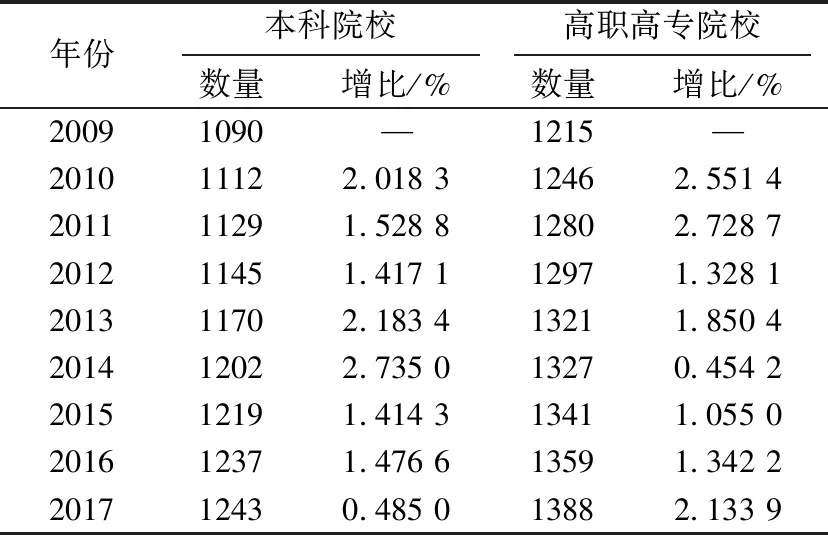
表 1 高等教育院校規模變化表

表3為高等教育在校生數量變化表，數據來源于教育部網站公布的2010～2017年全國教育事業發展統計公報[13～20].由表3可以看出:本科院校在校生數量比高職高專院校在校生數量多;本科院校在校生數量從2010年開始逐年上升，高職高專院校在校生數量從2010～2017年也穩步提升;在2013年以前，本科院校在校生增比要大于高職高專院校，自2014年以后，高職高專院校在校生增比幅度大于本科院校;就總體趨勢來看，本科院校在校生增比處于下滑趨勢，高職高專院校在校生增比呈上升趨勢.表1～表3中出現的增比指標按式(11)計算.

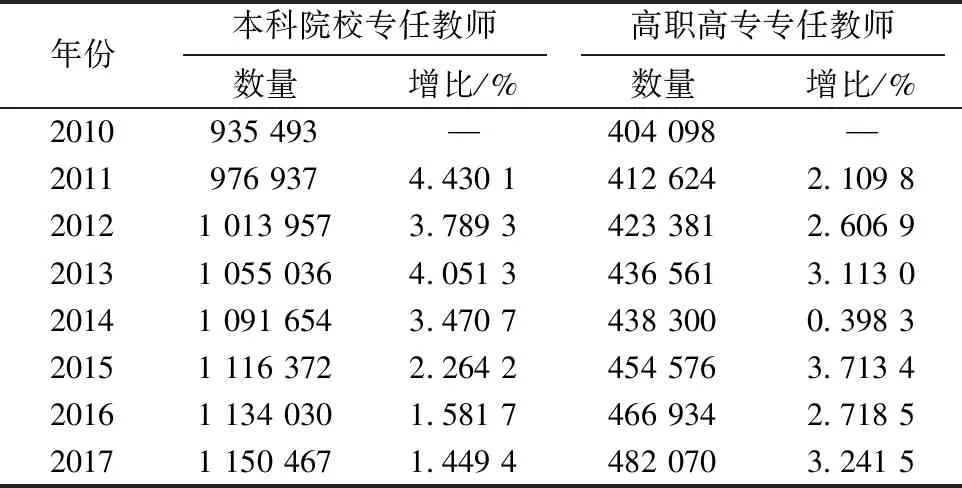
表 2 高等教育專任教師數量變化表

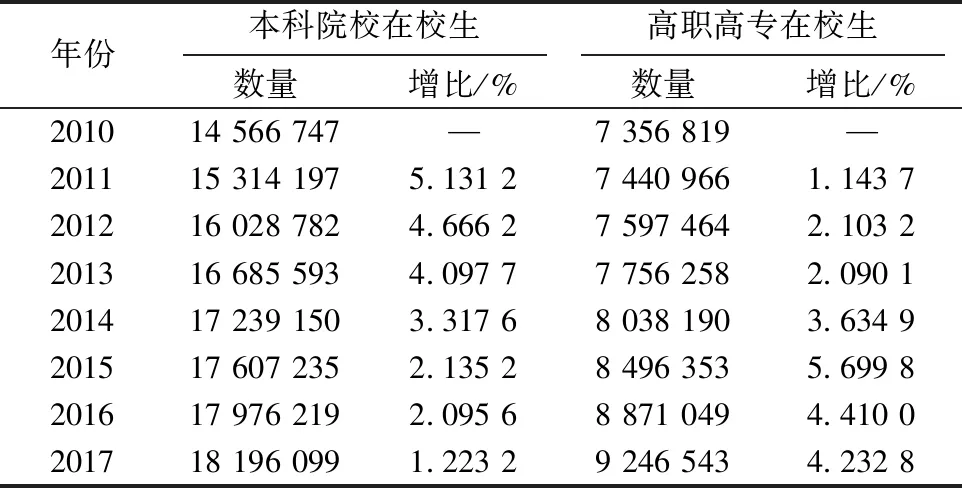
表 3 高等教育在校生數量變化表

3 ARIMA模型應用

本文從教育部2009～2017年度全國教育統計資料中獲取了高職高專院校規模、專任教師數量、在校生數量的基本數據，這些數據真實且按時間順序排列，具有時間序列特征，能夠反映某類現象的統計指標，且存在時間性和周期性，故借助應用比較成熟的時間序列模型ARIMA進行研究.

表4為高職高專院校專任教師數量數據的相關系數分布表，其中ACV表示自相關系數值，PACV表示偏自相關系數值.若自相關系數值在標準差寬度范圍內，則表明數據落入隨機區間內部，為穩定的時間序列.初始分布的標準差寬度為0.39，一階差分的標準差寬度為0.54.由表4得出，初始的ACV在滯后6階時，自相關系數值在隨機區間外部，需要對初始數據進行差分處理.一階差分后的自相關系數和偏自相關系數若全部落入隨機區間內部，經一階差分后的數據為平穩時間序列，那么自回歸分量階數p為0，差分次數d為1，移動平均分量階數q為0，那么選用的時間序列模型為ARIMA(0,1,0).

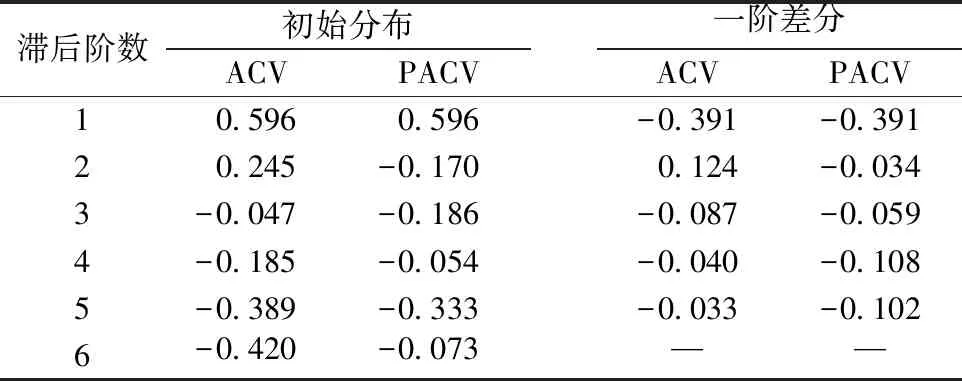
表 4 高職高專院校專任教師數量數據的相關系數分布表

表5為高職高專院校在校生數量數據的相關系數分布表.初始分布、一階差分和二階差分的標準差寬度分別為0.36、0.45和0.56.由表5可知:第1階、第5階和第6階自相關系數值在隨機區間外部，數據為不平穩的時間序列；第1階偏自相關系數在隨機區間的外部，從第2階起全部落入隨機區間內部，表現出截尾性，自回歸分量階數p為1.但是，已由自相關圖判斷出該數據為非平穩時間序列，需要進行平穩化處理.經一階差分后，滯后第1階和第4階的自相關系數在隨機區間外部，則移動平均分量階數q為4，滯后第2階及以后的偏自相關系數均落入隨機區間內部，則差分次數d為1，自回歸分量階數p為1，那么選用的時間序列模型為ARIMA(1，1，4).考慮到收集樣本數量較少，滯后階數過多可能影響預測結果的準確度，本文將對一階差分后的數據再次進行差分處理.二階差分后，所有階數的自相關系數和偏相關系數均落入隨機區間內，呈拖尾性，經二階差分后的數據為平穩時間序列，自回歸分量階數p為0，差分次數d為2，移動平均分量階數q為0，則選用的時間序列模型為ARIMA(0,2,0).

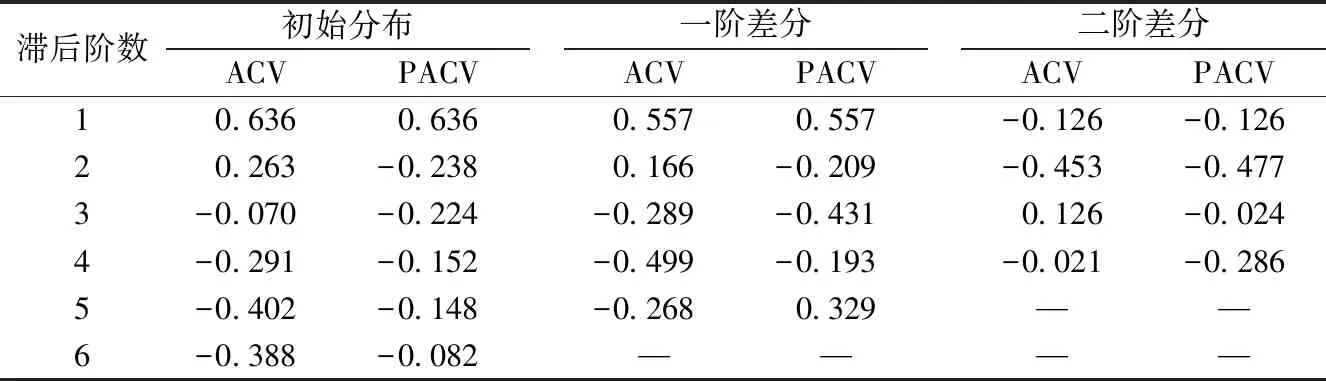
表 5 高職高專院校在校生數量數據的相關系數分布表

4 預測結果分析

通過ARIMA(0,1,0)模型對高職高專院校專任教師數量進行時序分析，其預測結果如表6所示，下限值指的是置信區間下限，上限值指的是置信區間上限.由表6可知，預測模型結果均在顯著性水平0.05的置信區間內，預測結果具有較高的可信度.預測結果顯示,2018年、2019年和2020年的專任教師數量分別為488 748人、499 613人和510 478人.從整體分布情況來看，高職高專院校專任教師數量在未來幾年依然會保持持續增長的趨勢.通過ARIMA(0,2,0)模型對高職高專院校在校生數量進行時序分析，其預測結果如表6所示，預測模型結果均在顯著性水平0.05的置信區間內，具有較高的可信度。預測結果顯示，2018年、2019年和2020年在校生數量分別為9 622 037人、9 997 531人和10 373 025人.從整體分布來看，高職高專院校在校生數量在未來幾年依然保持持續增長態勢.值得說明的是，為考察專任教師和在校生數量預測值的可信度，進行了相對誤差百分比的評價計算，從數值上來看均不到5%，表明預測結果滿足預測精度.

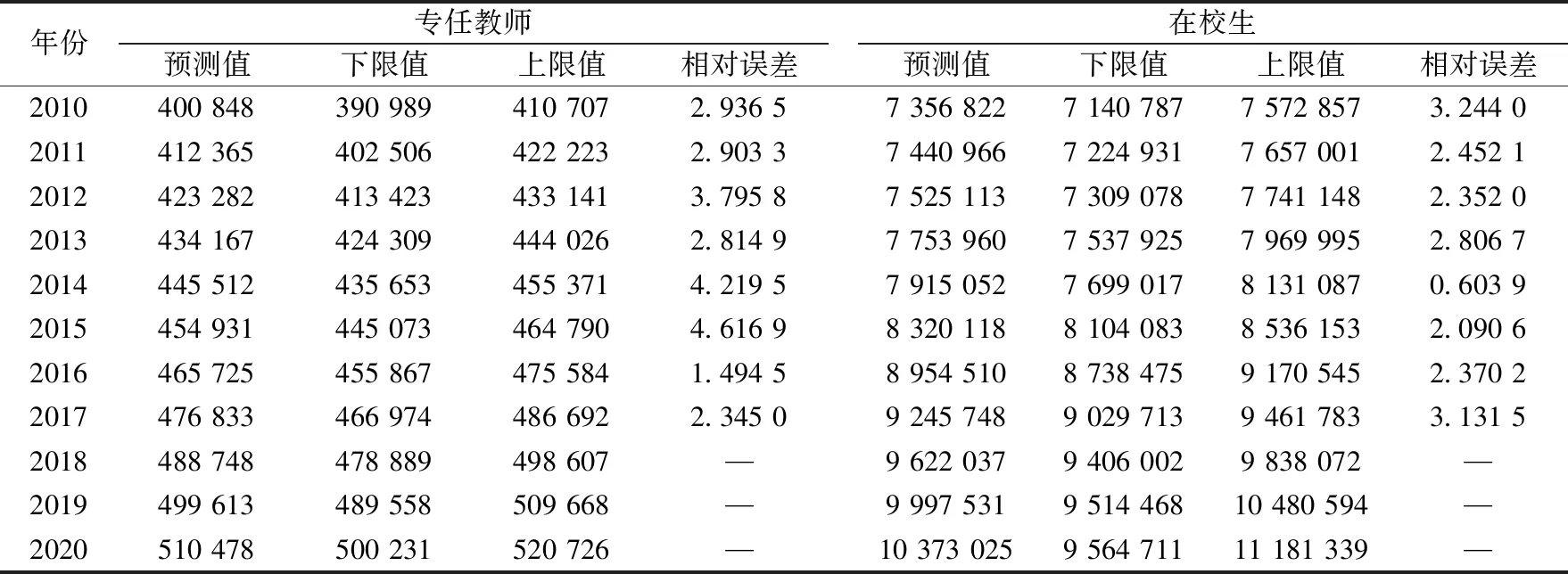
表 6 高職高專院校專任教師和在校生預測結果表

普通高校生師比定義為在校生數量與專任教師數量之比，教育部[2004]2號文件規定高等教育院校生師比的標準為18∶1，本文通過ARIMA模型預測結果計算了未來幾年高職高專院校的生師比，如表7所示，給出了高等教育院校生師比預測值對照結果.由表7可以看出：本科院校的生師比一直低于16∶1；高職高專院校生師比在2013年以前基本上接近于18∶1，但從2014年開始增速加快，在2017年生師比達到19.18∶1.預測模型結果顯示：2018年生師比為19.69∶1，2019年生師比為20.01∶1，2020年生師比位20.32∶1.生師比是判斷世界頂尖大學的基本標準.泰晤士報上的大學排名，把生師比作為考量的重要指標.英國《獨立報》編輯湯姆·門德爾松說過，“一所大學的學者越多，學生就會得到更多的關注，那么學生與教師的交流頻率更多，他們在學習過程也會獲得更有價值的內容”.創建一流的大學需要一流的師資力量，生師比數據就是一個需要考量的關鍵指標，教師越多，所營造的學術氛圍和教學環境越好.英國《衛報》認為：生師比應考慮的是從事教學工作的教職員工，不包括從事少許教學工作的研究人員.生師比是反映大學教學質量的重要指標，良好的生師比是提升高職高專學生就業質量的基礎保障.在未來的幾年里，高職高專院校還需要保障良好的師資團隊，控制生師比，為高職高專院校的可持續發展提供基本的保障.

表 7 高等教育院校生師比預測值對照表

5 結論

高職高專院校的生師比指標關乎學校教育的質量，合格生師比指標為18∶1，限制招生生師比指標為22∶1.本文結合時間序列ARIMA模型對高職高專院校未來幾年的生師比進行預測，得出結論如下：(1)就整體趨勢而言，高職高專院校數量增幅較快，且其專任教師和在校生數量增比要高過于本科院校；(2)初始的高職高專院校教育統計數據是真實的，具有時間序列特征，但是多數為不穩定時間序列，需要進行一階或二階差分處理；(3)高職高專院校2018年生師比為19.69∶1，2019年生師比為20.01∶1，2020年生師比為20.32∶1.結果表明：未來幾年內高職高專院校生師比呈上升趨勢，將超過合格指標，為師資隊伍建設及制定招生計劃提供理論參考.