基于數學表征的小學數學錯題類型及對策研究

[摘 要] 低年級學生數學表征能力低，面對數學問題易產生解題困惑。針對低年級學生數學解題能力薄弱的現狀，對數學錯誤開展研究。在調查分析學生目前數學錯題類型的基礎上，以數學表征理論為基礎，分析各領域錯題的成因，提出了提升數學表征水平的教學建議。

[關鍵詞] 數學表征;小學數學;數學錯題

[作者簡介] 張夢茜（1995—），女，江蘇蘇州人，碩士學歷，上海市華江小學初級教師，研究方向：小學數學。

[中圖分類號] G622? ? [文獻標識碼] A? ? [文章編號] 1674-9324（2020）31-0001-03? ? [收稿日期] 2020-02-11

小學低年級在整個義務教育階段處于根基，學生開始學習日常生活中需要的數學，也就是計數、度量并解決簡單的實際問題[1]。低年級學生數學表征水平不高，數學知識被學生內化后在頭腦中的表征往往不像教材上的知識那樣脈絡分明，難以擺脫以表現為憑借的具體形象表征[2]。目前基于表征水平視角下有關小學生錯題的分析還不多，本文就數學學習起步階段的錯題類型及成因進行分析，探究小學低年級學生表征水平現狀。

一、小學低年級數學錯題類型

研究主要采用調查研究的方法。根據上海市小學生學習數學知識的板塊，將此次調查分為三個領域，分別是計算、概念、問題解決。被試學校為上海市一所公辦小學，教學成績在該區公辦小學中處于中上等水平，被試家庭的社會經濟狀況處于該區中等水平。研究者依據一年級小學生的數學學習水平對其進行測試，有效統計被試人數為277人。

（一）計算領域

此次測試計算領域涉及20以內不進位加法和不退位減法、20以內進位加法和退位減法以及20以內數和算式大小的比較等內容。根據各領域的測試內容，統計該部分測試內容的主要錯誤類型、各錯誤類型占此類型題目錯誤總數的百分比，其中有部分學生會在同類型測試內容中出現兩種或兩種以上的錯誤類型。

從表1可以看出，在20以內加減法中，占比最多的是變式計算中運算順序錯。變式口算貫穿整個小學階段，平時練習中口算的運算順序掌握后，一旦出現變式口算練習，學生會出現從右往左計算的錯誤。符號識別錯誤在加減法計算中占比達23.07%。數和算式大小的比較中，錯誤類型最多的是計算錯誤，加減法中變式計算產生困難的學生在此通常也會產生錯誤。

（二）概念運用

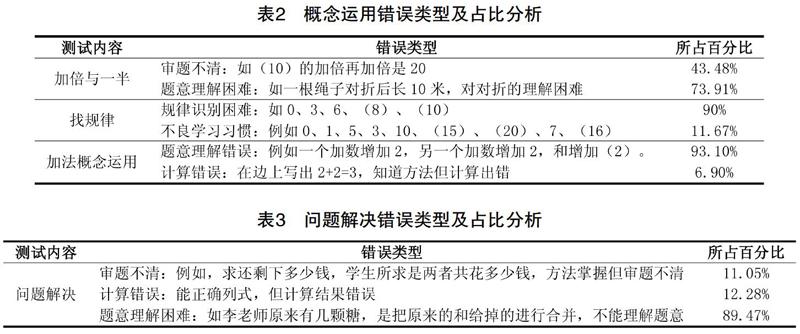
概念運用部分涉及加倍與一半、找規律、加法概念運用等題目，為了區分學生的表征水平設計的題目均有一定難度。試題能反映學生的多種表征方式及思維的多角度性，例如：一根繩子對折后長10米，這根繩子原來長（? ）米;（? ）的加倍再加倍是20等。

在加倍與一半內容中，同時產生兩種類型錯誤的人數最多，其中大部分學生是由于題意理解困難而產生錯誤，另有43.48%的學生是由于審題不清做錯的。在找規律內容不少學生對于不那么明顯的規律顯然是有些束手無策。加法概念并不是直接給出算式口算，而是根據加法各部分名稱及含義進行解答，學生因題意理解錯誤的出錯率較高。

（三）問題解決

滬教版的教材所選材料貼近學生的生活現實，在教材和平時課堂中注重從生活中發現和提出簡單的數學問題[3]。此次測試安排的內容有合并問題、求部分問題、加減混合問題等。由于問題解決部分所涉及的錯誤類型是有共通性的，所以僅進行問題解決部分的錯誤分類，不再細化。

此次測試的問題情境都貼近學生的生活，是學生在日常生活中所接觸過的。問題呈現的情境與學生的知識經驗較為接近，可以讓學生在其中尋找解決問題的線索[4]。小學低年級所涉及的問題解決類型雖是有限的，但從中能看出不少問題。由于學生情境表征、圖式表征等發展不足，問題解決領域出現的錯誤較多。

二、基于數學表征錯題成因分析

（一）計算領域錯題成因分析

1.具體形象思維較重，符號表征局限于淺層。低年級學生才開始接觸數學符號，對“+”、“-”符號的含義還沒有形成固定的模式。在變式口算中，低年級學生較易產生錯誤，除了對運算順序掌握的熟練程度外，另一個重要原因是變式口算中存在大量用符號表示數的情況，如：（? ）+5=9。在此題中，（? ）表示其中一個未知的加數。

2.不能正確把握數學知識的因果關系，關系表征處于較低水平。數學是一門研究“關系”的學問，整數加減法的學習還與學生的歸納、概括、推理能力的發展相關，這涉及學生關系表征的發展水平。數學運算的產生源于事物數量間關系的分析處理，例如，減數小于或等于被減數，其含義是集合A對它的子集B作差集時所得出的基數。關系表征發展水平低的學生無法正確解題。

3.思維變通性缺陷，語詞表征發展不成熟。低年級學生詞匯量較少，雖然此次測試由測試者依次讀題，但對題目表達的具體含義理解是有困難的。如在比大小中讓學生在（? ）中填上最大的數時，有不少學生僅填上了合適的數。

（二）概念運用錯題成因分析

1.數學知識間的練習呈間斷狀態，關系表征的發展尚未成熟。與計算領域一樣，概念運用具有較高的邏輯性。如“一根繩子對折后長10米，原來長多少米”，這類問題體現了數學的推理和結論的嚴密性。關系表征要求學生把握事物的抽象關系，對事物種屬關系及經驗的因果關系進行分析和理解。

2.由于年齡特征和知識水平，方法表征具有局限性。數學學科具有高度的系統性，知識銜接緊密，其完整、嚴密的特點需要學生具有良好的方法表征水平。對于運算要求有一定的合理性，對于知識的宏觀層面，需要學生使用方法表征進行內部再現。

3.高級表征方式的缺乏。概念運用產生錯誤的學生，數學表征處于較低水平。數學的一個突出特點是高度概括和抽象數量關系及空間形式[5]，這種抽象的特點要求學生具有圖式表征、符號表征等高級表征方式。低級表征方式不進一步發展，會產生解題障礙。

（三）問題解決錯題成因分析

1.不能結合數學知識與生活經驗，解題時缺乏情境表征。良好的情景表征能夠幫助學生將題目中的信息抽象成具體的情境。解題成功的學生頭腦中的情景較為豐富，且有一定結構化、層次化，便于提取和運用，在此基礎上進行分析更易獲得解題成功。解題錯誤者對于情境的描述是錯誤的。

2.不能選擇合理的方法解題，圖式表征發展緩慢。圖式表征以畫簡圖的方式建立問題的視-空模型和其中的數量關系圖式，采用這種表征能夠直接跳過中間的情境表征環節，直接進入問題解決過程。學生可以在空白處用畫簡圖的方式達到對題意的理解。圖式表征水平較低的學生不能準確根據題意畫圖，甚至由于缺乏應變能力不能選擇此類表征方式。

3.脫離具體實物的符號表征水平較低。在圖式表征的基礎上，抽象表征方式發展較好的學生會抽象出數學對象的本質，在解題中用數學符號表示數學對象。此次測驗的問題解決并不都是平時學生接觸的類型，學生在面對復雜異于所熟知的數學問題時會感到掙扎，因為在學校教授的策略僅需要找到并應用正確的公式或策略來回答結構良好的算法問題[6]，而符號表征能夠幫助學生發展解決結構異常的問題的能力。

通過對數學學習優秀學生和困難學生的比較研究還發現：數學學習困難者表征方式較為單一，與優秀學生有一定差距。良好的數學表征方式能夠將問題解決最重要的部分及數量關系放在突出位置。比較而言，學習優秀者偏向于選擇圖式表征、關系表征、符號表征，對于數學問題中信息的表征較為全面和準確;數學學習困難學生偏向于使用語詞表征、關系表征，較為關注數學問題中局部的細節，缺乏問題整體性的把握。高級表征方式能夠幫助學生在思維過程中以判斷、推理的形式，反映數學問題的本質屬性和內在的規律。

三、思考與建議

數學表征是整理數學信息、形成結構思想的重要手段。提升數學表征水平，促進學生數學表征多樣化，是義務教育階段教師需要重視的。在教學中，要有目的、有計劃地對學生的數學表征進行訓練，踏踏實實把提升表征水平的工作貫穿到數學學習的全過程中。

（一）在數學基本活動中促進數學表征抽象發展

數學基本活動經驗源于日常生活經驗，并在此基礎上升華。活動中，首先，需要有明確的數學目標，指導學生對具體實物操作、觀察與思考，借助直觀模型分析數量間的關系是感知認識的基礎[7]。其次，數學現實是表層的經驗活動，從與生活直接相關的現實出發，逐步引導學生抽象表征，脫離生活原型到達上層的數學現實。有了對數學現實的完整認識過程，鼓勵學生使用其他表征方式闡述對數學現實的認識，促進數學表征多元化。

（二）在數學問題解決中鍛煉學生高級表征能力

文字表達的數學問題涉及生活相關的數學情境或模擬情景，且融合于各個領域之中。這些關于數的擴展的問題應用于現實，與之相關的是關系表征、符號表征等高級表征的能力。數學課堂中要注重數學情境的多元化，以數量相依關系，采用形式化的數學符號和語言，以關系表征和符號表征的方式表達出數學結構[8]。低年級學生使用最多的是關系表征，關系表征是用科學的抽象概念揭示事物的本質表達，認識數學問題的結果。解題時關系表征往往不會單獨出現，與之相伴的是符號表征。從解決問題方法多樣性的角度出發，畫實物圖、列表的方法都可以成功解題;從數學表征水平出發，使用抽象的符號表征解決問題更具有一般性，是較高層次的思維發展。小學低年級已經大量出現符號表征，如數的運算、大于等于小于、用Ο￡表示數或公式等。培養學生習慣、喜歡和善于運用符號表征，是提升學生高級表征能力的重要方面。

（三）從多角度、多方面、多維度進行多元表征

小學低年級學生對于數學內容的理解呈孤僻、間斷狀態。對于數學知識的理解，如概念、公式、符號停留在表象的理解，知識間的串聯是忽視的，重內涵而輕外延，因此多元表征也是反映學生思維品質的重要方面。教師要幫助學生逐步建立和完善思維的整理結構、知識的整體架構，準確把握數學知識之間的因果關系。多元表征會幫助學生進行綜合推理。教師在教學時可以引導學生使用關系表征理清邏輯線索，將問題的條件和中間環節緊密串聯，再使用符號表征恰當選擇數學符號。借助符號可以將邏輯關系表現得簡單明了，保證推理運算的有效進行[9]。

參考文獻

[1][7]張奠宙.小學數學研究[M].北京：高等教育出版社，2009.

[2]張夢茜.小學數學“解決問題的策略”表征水平的研究[D].揚州：揚州大學，2019.

[3]中華人民共和國教育部.數學課程標準（2011年版）[M].北京：人民教育出版社，2011：11.

[4]張夢茜.小學數學高年級“圖形與幾何”錯題類型分析及對策研究[J].數學學習與研究，2018（24）：125.

[5]劉翔平.學習障礙兒童的心理與教育[M].北京：中國輕工業出版社，2019：125.

[6]C.A.Ogilvie.Changes in students' problem-solving strategies in a course that includes context-rich，multifaceted problems[J].Physics education research，2009（5）：2.

[8][9]孔凡哲，曾崢.數學學習心理學[M].北京：北京大學出版社，2012.