基于多層卷積網絡的圓弧快速檢測算法設計

張智凡，于鳳芹

(江南大學 物聯網工程學院，江蘇 無錫 214000)

0 引 言

圖像處理技術在地理信息、建筑、電子、機械等領域中得到了廣泛應用，特別是對工程圖紙的理解與識別過程，更是極大地依賴于圖像處理技術[1]。而在工程圖紙理解與識別中，最主要的基礎圖元就是圓弧，因此對圓弧進行準確迅速的檢測是工程圖紙理解與識別領域的一個關鍵問題，也是工件尺寸測量領域的一個重要問題[2]。

圓弧檢測的基礎算法是霍夫變換算法。隨機霍夫變換可以克服計算量大[3]、占用內存大、無法在線實時檢測的缺點，但是由于隨機抽樣會產生很多無效點集，會增加搜索時間并且降低在復雜背景圖像中的檢測效率和精度[4]。概率霍夫變換可以解決前兩種算法耗時的問題，在選擇擬合點時采用了隨機抽取的方式，并加入了計數器，當直線被擬合出的次數達到一定閾值時取出這條線并完成擬合，增加了檢測實時性[5]。有學者在霍夫變換算法的基礎上提出了一系列優化的圓弧檢測算法，文獻[6]通過找出可能位于圓外邊界上與圓相切的線段，根據切線段估計圓心半徑，得到候選圓集合并進行數據合并，對每一個候選圓進行跟蹤檢測來判斷其為圓或弧。但該方法在匹配切線的過程中確定候選圓，易導致誤檢情況的發生。文獻[7]提出了一種利用統一多尺度深卷積神經網絡進行快速目標檢測的方法，但是該方法的檢測精度存在一定的影響范圍，難以保證整體的高準確性。文獻[8]利用確定的橢圓中心為匹配參考點逐行匹配圓弧特征點，然后利用改進的RANSAC算法排除誤匹配對，但是計算量大，匹配成功率偏低。

針對現有方法中存在的誤檢率較高、檢測效率低的問題，文中提出一種基于多層卷積網絡的圓弧快速檢測算法，以提高圓弧檢測算法的計算效率與準確度。首先基于多層卷積網絡進行圓弧信息的聚類存儲，并將缺損比例在三分之一以下的圓弧排除，再對其他圓弧進行全局聚類。該過程減小了噪聲和缺損圓弧的干擾，提高了圓弧檢測效率。然后以圓弧的圓心所在區域為依據對圓心閾值區域進行重構，獲取圓弧閾值區間。最后對閾值區間進行優化，并對圓弧進行擬合和去偽，實現圓弧的快速檢測。

1 基于多層卷積網絡的圓弧快速檢測算法設計

1.1 圓弧檢測原理

大量物體具有圓弧輪廓，可以通過檢測圓弧來識別物體的存在，并可利用其實現產品質量評估、提高生產效率等。圓弧檢測的基本原理是在對圓弧圖像識別的基礎上，對圓弧特征信息進行提取、儲存、分析和判斷，并優化霍夫變換算法，實現對圓弧的檢測。

一般情況下，對圓弧圖像的識別需借助機器視覺技術，其識別過程如圖1所示。

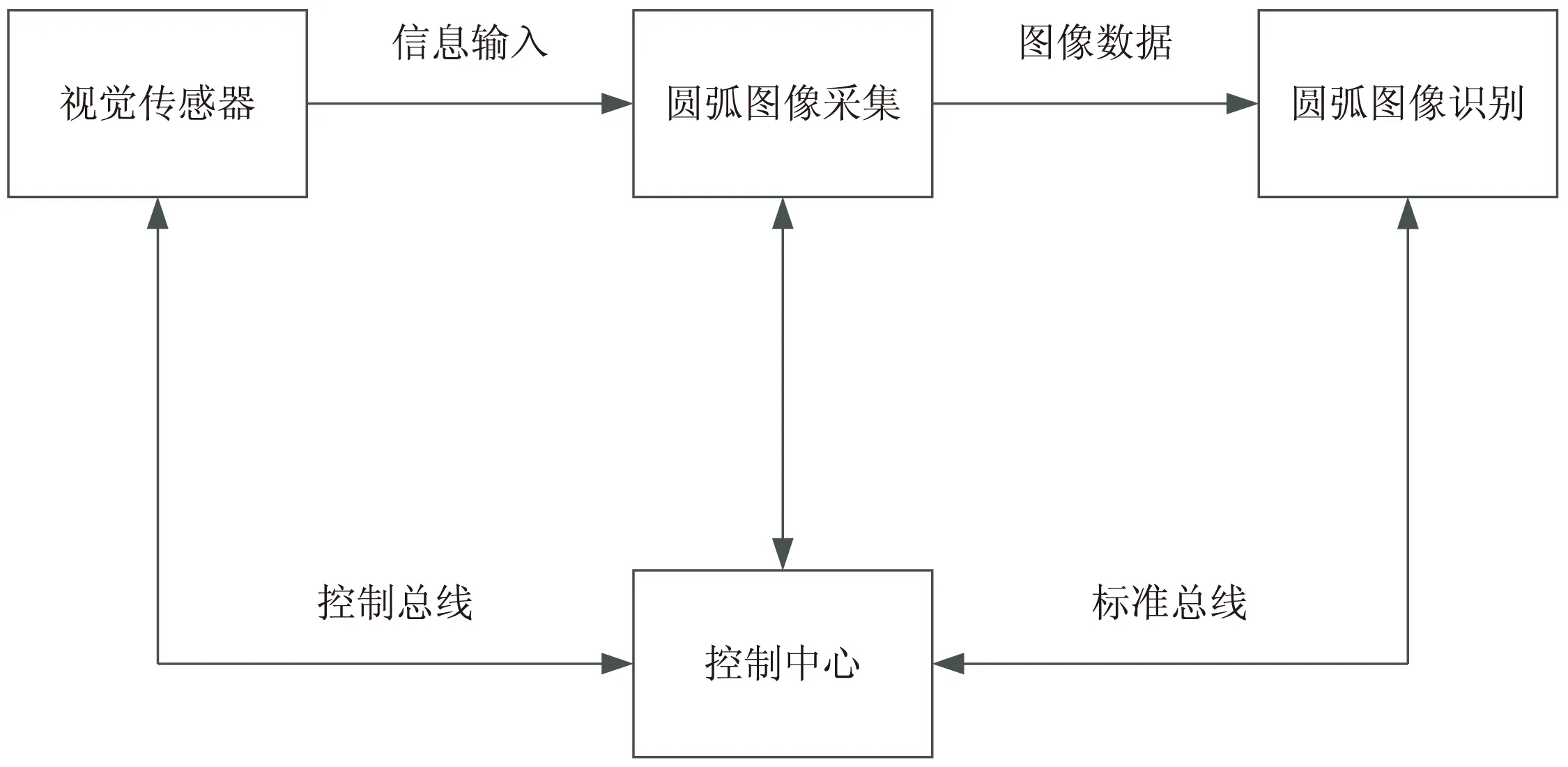
圖1 基于機器視覺技術的圓弧圖像識別過程

在此基礎上，從機器視覺的識別結果中提取圓弧的特征信息，并將其中夾雜的噪聲濾除，對目標圖像的信息加強，再對其進行提取、儲存、分析和判斷，繼而對基礎的霍夫變換算法進行優化，完成對圓弧信息的檢測。其中，霍夫變換算法是利用圖像空間和霍夫參數空間的線-點對偶性，把圖像檢測過程由圖像空間轉換到參數空間中進行。

1.2 基于多層卷積網絡的特征點提取及圓弧信息的聚類存儲

首先利用多層卷積網絡實現圓弧信息的聚類存儲[9]。多層卷積網絡是一種可用于進行圖像特征識別的感知器模型，其中包括卷積層、Maxout層、池化層和全連接層。其中，卷積層用于提取特征，Maxout層利用Maxout激活函數實現信息篩選，池化層用于選擇特征，全連接層用于分類。在多層卷積網絡中，在兩個及以上的卷積層后才會存在一個池化層，即卷積層串聯。這是一種優化操作，即通過增加卷積層數來縮小卷積核的尺寸，從而減少網絡參數，增加多層卷積層中的非線性操作，使多層卷積網絡對特征信息的學習能力更強。

利用多層卷積網絡對圓弧信息進行訓練，從中提取圓弧的特征信息，并以此為依據對圓弧信息進行聚類存儲[10]，具體步驟如下：

①利用卷積核掃描所輸入的圖像，逐個掃描圖像中的所有像素點。在掃描過程中將最先找到的特征像素點記錄為p，并自上而下對其進行初始化檢測，規定其初始化值為0[11]。

②分別檢測p上方位的右、中、左三個位置，當檢測到對應位置的特征像素點后將其記錄為q1，并在數組中儲存q1的坐標位置，將其像素值初始化為0。對p左、右兩方位的像素點進行檢測，檢測到像素點后對其進行標記并儲存坐標點位置，檢測不到像素點時則退出聚類[12]。

③分別檢測p下方位的右、中、左三個位置，當檢測到對應位置的像素點后將其記錄為q2，并在數組中儲存q2的坐標位置，將其像素值初始化為0。按照步驟②中的方法對q2的左、右兩方位的像素點進行檢測。

④分別對p左、右兩個方位的像素點進行檢測，將檢測到的像素點分別記錄為q3、q4，并在數組中存儲q3、q4的坐標位置，將其像素值初始化為0。按照步驟②中的方法對q3、q4的8個方位的像素點進行檢測。

⑤以方位標記為依據，當方位標記是上方位時，進行步驟②的操作，當方位標記是下方位時進行步驟③的操作，當方位標記是左右方位時進行步驟④的操作[13]。

不斷重復上述步驟即可在卷積層中得到圓弧圖像的特征信息，經過Maxout激活函數篩選得到特征圖，然后在池化層池化這些特征。池化操作是為了進一步減少網絡參數，防止多層卷積神經網絡過擬合。然后在全連接層輸出標記特征結果，如下所示：

(1)

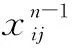
根據上述特征輸出結果進行聚類及存儲，其過程如下：

·隨機選取k個特征像素點作為初始中心點，即共有k個類；

·計算其余特征像素點到這k個中心點的距離，從中選擇距離最小的中心點；

·重新計算k類的質心作為新的中心點；

·迭代步驟2和3，直到達到最大的迭代次數，輸出聚類中心集并在數組中存儲。這樣，通過聚類方向自帶的慣性作用即可加速圓弧的檢測，并且能夠將數目較少的孤立像素點當做噪聲信息直接過濾[14]。

1.3 圓弧全局聚類

完成圓弧信息的聚類存儲后，對圓弧進行全局聚類，即把不相接的、一個橢圓中的圓弧劃分至一處。將缺損比例在三分之一以下的圓弧排除，對其他圓弧進行全局聚類，聚類依據為包含像素點的具體數量。如圖2所示，圓弧a1為待聚類的對象，首先對a1的搜索區域進行定義，對圓弧a1與搜索區域中的圓弧進行全局聚類。該搜索區域的定義為圓弧a1的弦J3、J4,切線τ1、τ2以及圖像邊界所構成的區域。接下來對搜索區域內能夠與圓弧a1進行全局聚類的其他圓弧進行搜索：過圓弧a1的末端點與首端點作與J3、J4平行的直線，當該直線與切線τ1、τ2相交時可獲得兩個交點，當其他圓弧的首端點與末端點都位于搜索區域之內，即說明該圓弧位于圓弧a1的搜索區域內[15]。

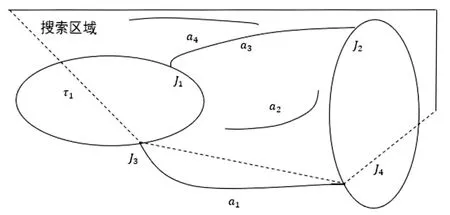
圖2 圓弧搜索區域定義

利用弧中心、弦中心距離條件對圓弧是否屬于同一橢圓進行確定：

(2)

‖Pm/2,1Pn/2,2‖>‖C2Pm/2,1‖

(3)

如圖3所示，C1、C2、C3分別代表弦b1、b2、b3的中點;Pm/2,1、Pn/2,2、Ps/2,3分別代表圓弧a1、a2、a3的中點;m、n、s分別代表圓弧a1、a2、a3的點數，當下標不能整除時可進行四舍五入。通過式(2)、式(3)可排除搜索區域內不屬于一個橢圓的圓弧。

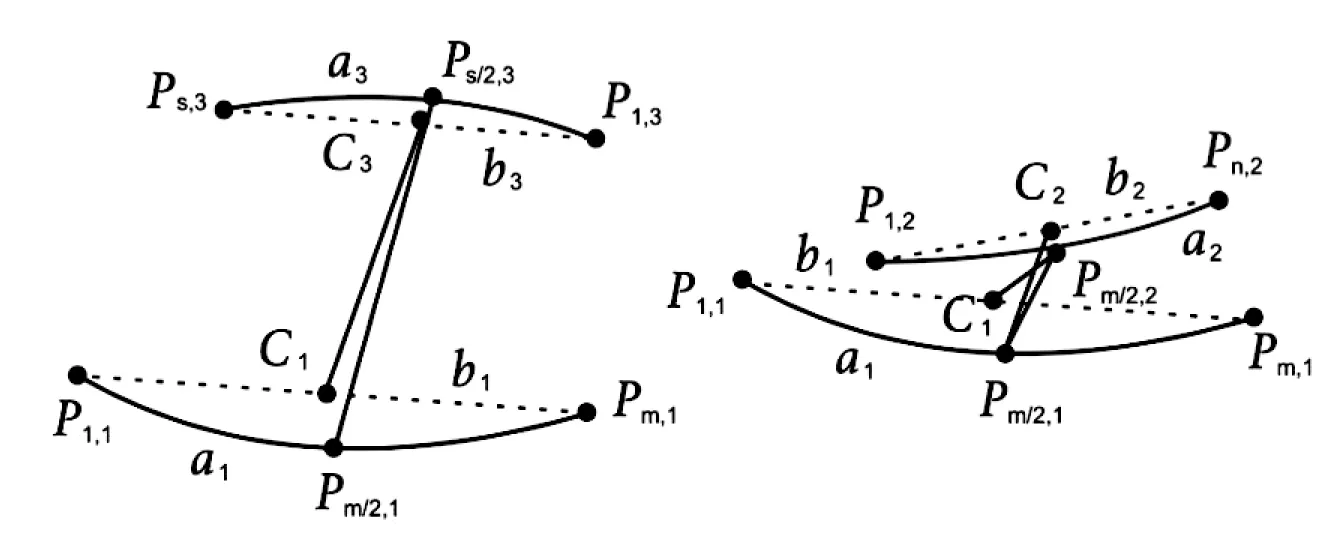
圖3 去除圓弧a2

1.4 圓弧閾值區間的獲取、優化

完成圓弧全局聚類后，對其進行閾值區間獲取[16]。以圓弧的圓心所在區域為依據對圓心閾值區域進行重構：在數組中利用三弦比例對圓弧上最短的采樣點間隔長度進行確定，并按照順序獲得n組采樣點以對圓心分布區域進行計算，其中分布如圖4所示。在計算時，每次都需要在參數空間中對對應的格子累加器進行加一操作。對參數空間中持有最大累加值的格子位置進行統計即可獲得圓弧的圓心所在區域。對該區域的縱坐標與橫坐標進行分布范圍記錄，以計算圓心區域的構筑邊長，計算公式如下：

(4)

其中，L表示圓心區域的構筑邊長；H表示橫坐標分布范圍的差值；V表示縱坐標分布范圍的差值；Hu、Hb表示橫坐分布范圍的橫縱坐標；Vu、Vb表示縱坐標。構筑以圓心為中心，邊長為L的正方形區域即為圓弧的閾值區間。

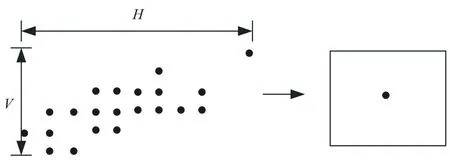
圖4 閾值區間示意圖

完成圓弧閾值區間獲取后，需要對其閾值區間進行優化，并對圓弧進行擬合和去偽，以實現圓弧的快速檢測[17]。其中閾值區間的優化策略如表1所示。

表1 閾值區間優化策略

而圓弧的擬合和去偽需要對候選弧對與圓弧的有向邊界列進行提取，并利用最小二乘法對候選圓的參數(p,q,r1,r2,θ)進行計算。并對候選圓上是否存在邊界像素進行判斷：

(5)

當di的值不屬于圓弧的閾值區間時，將候選圓排除。直到各個圓弧都找到對應的圓，完成圓弧的擬合和去偽，實現圓弧的快速檢測。

1.5 基于多層卷積網絡的圓弧快速檢測算法步驟

基于多層卷積網絡的圓弧快速檢測算法的檢測過程如圖5所示。

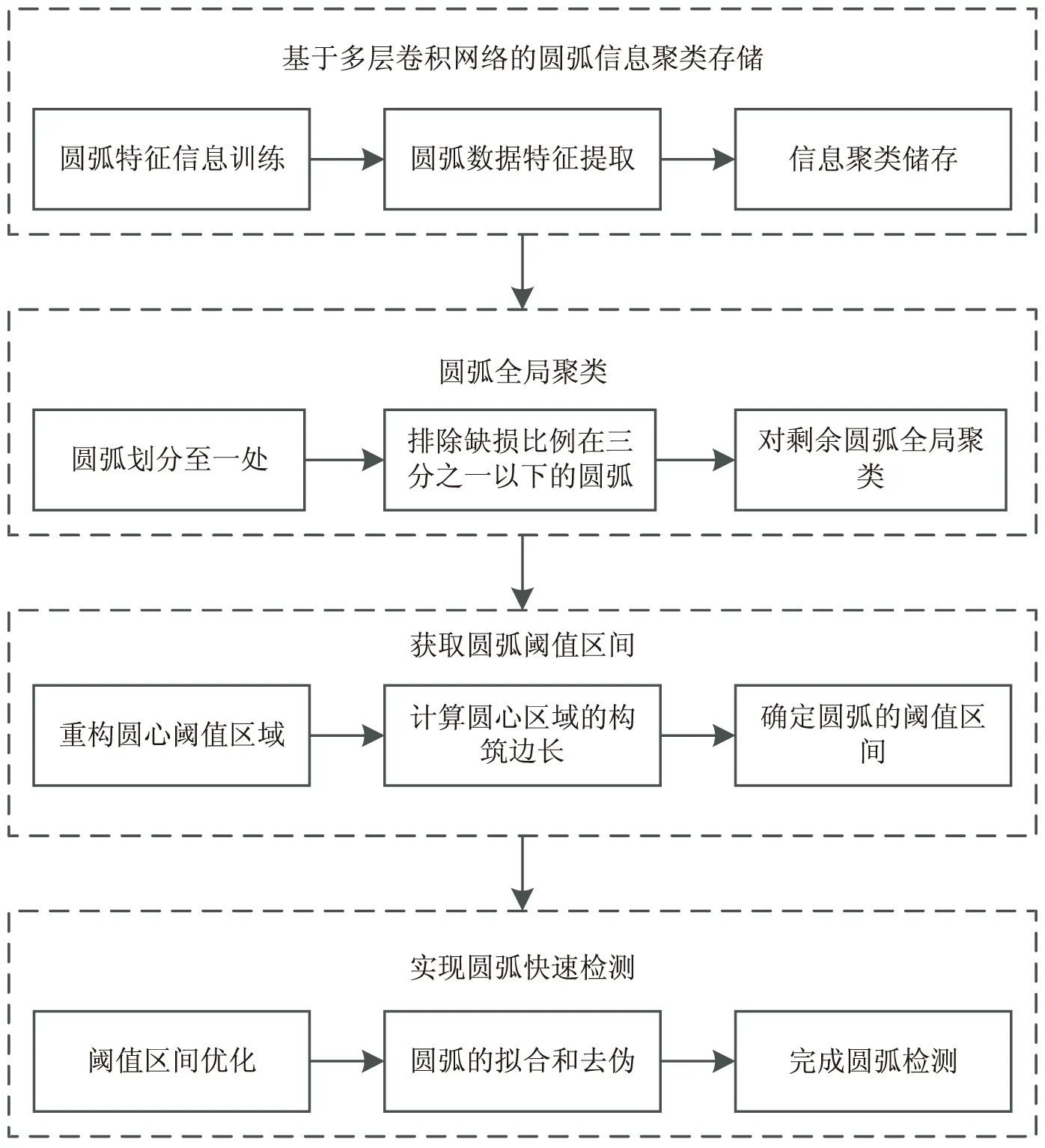
圖5 基于多層卷積網絡的圓弧快速檢測過程示意圖

根據圖5可知，所設計的基于多層卷積網絡的圓弧快速檢測算法首先是借助于多層卷積網絡實現了圓弧信息的聚類存儲，然后利用圓弧聚類方向自帶的慣性作用將數目較少的孤立像素點過濾掉，并對其他圓弧進行全局聚類。在此基礎上重構圓心閾值區域，獲取圓弧閾值區間，并對閾值區間進行優化，對圓弧進行擬合和去偽，完成對圓弧的快速檢測。

2 仿真實驗結果與分析

為了檢測提出的基于多層卷積網絡的圓弧快速檢測算法的有效性，設計如下實驗，將該方法與文獻[6]中的基于切線段匹配的快速圓弧檢測算法、文獻[10]中的基于邊界聚類的圓弧檢測算法進行對比。

2.1 實驗環境

算法運行的環境為MATLAB 8.0的程序開發環境、Windows 7的操作系統、3G DDRII的內存、2G雙核處理器、Technology AMD Turion 的CPU。

在GREC2013測試集中對工件的擬合圖片進行選取，圖片尺寸為512×512，共6張，利用基于多層卷積網絡的圓弧快速檢測算法、基于切線段匹配的快速圓弧檢測算法和基于邊界聚類的圓弧檢測算法對其中的圓弧進行檢測，觀察不同算法的誤檢情況和檢測耗時，比較其性能的優劣。

2.2 實驗結果與分析

(1)誤檢率對比。

利用基于多層卷積網絡的圓弧快速檢測算法、基于切線段匹配的快速圓弧檢測算法和基于邊界聚類的圓弧檢測算法進行圓弧檢測的識別結果如圖6所示。

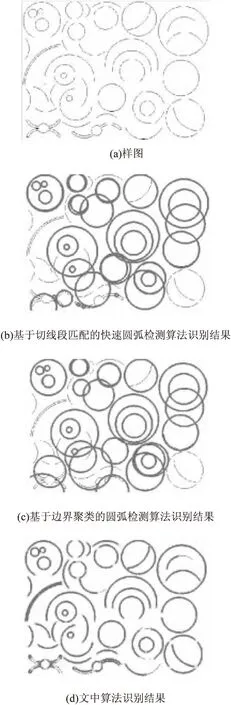
圖6 不同算法的檢測識別結果

分析圖6可知，文中所提算法的檢測結果明顯要優于另外兩種算法，檢測結果與樣圖相符，且噪聲較小、清晰度更高。

為進一步驗證所提算法的準確性，對比不同圓弧檢測算法的誤檢率，對比結果如表2所示。

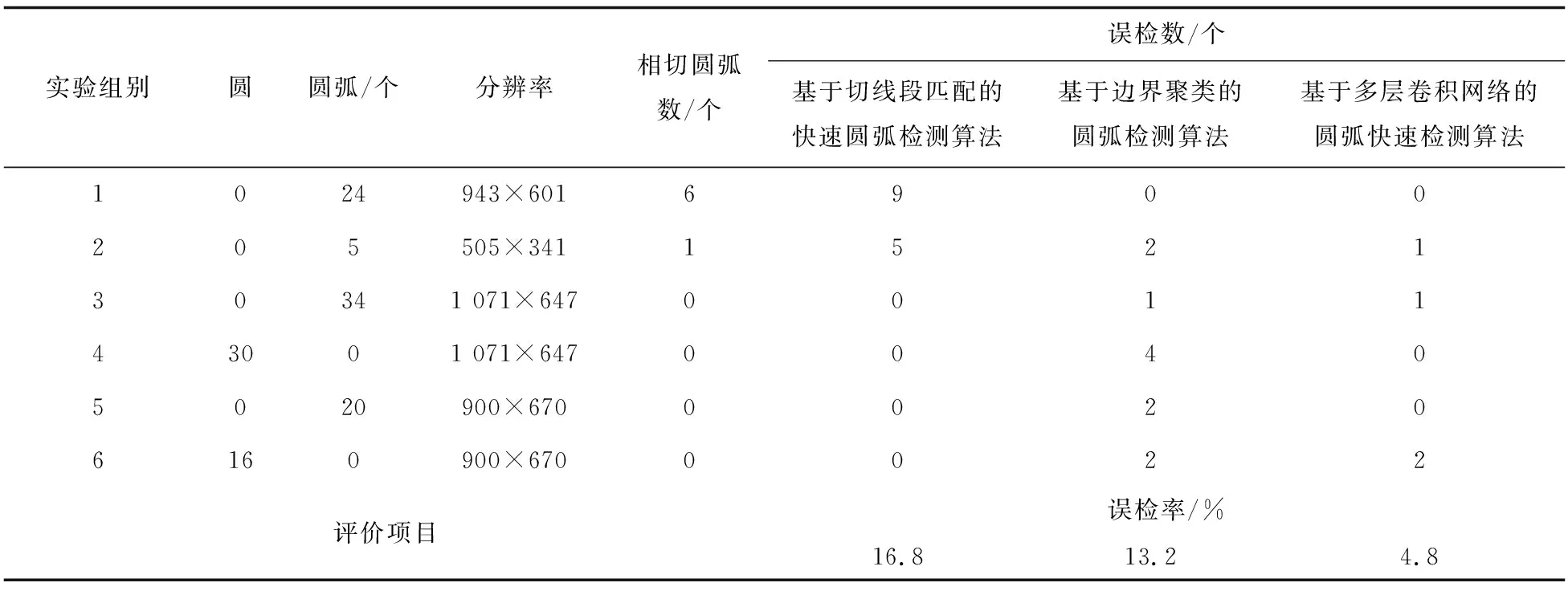
表2 誤檢率對比結果

根據表2中數據可知，基于切線段匹配的快速圓弧檢測算法的誤檢率為16.8%，基于邊界聚類的圓弧檢測算法的誤檢率為13.2%，基于多層卷積網絡的圓弧快速檢測算法的誤檢率為4.8%。通過比較可知，所提圓弧檢測算法的誤檢率在三種算法中最低，能夠實現對圓弧的準確檢測。

(2)檢測精度對比。

在一個目標檢測過程中，檢測結果的質量可從召回率和精度兩方面進行評價。召回率和精度成反比例關系，召回率越高則檢測精度越低。因此為驗證所提圓弧檢測算法檢測結果的精度，測試不同算法的召回率，得到對比結果如表3所示。

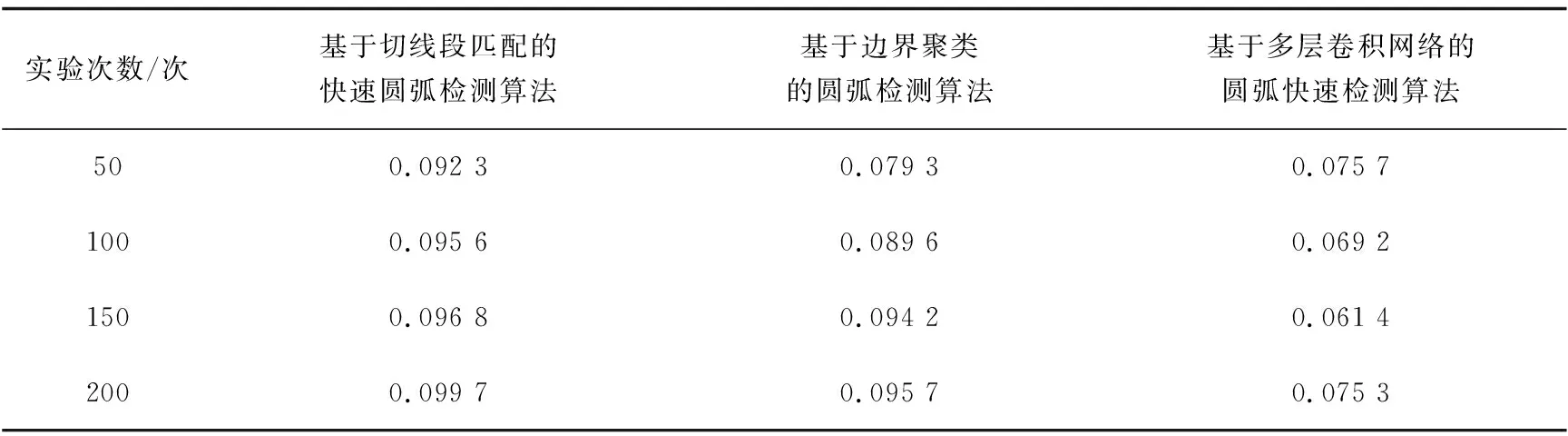
表3 不同圓弧檢測算法的召回率對比 %

分析表3可知，隨著迭代次數的增加，不同算法檢測結果的采集召回率也在不斷發生變化。基于邊界聚類的圓弧檢測算法召回率的變化幅度在三種算法中最大，但是召回率比基于切線段匹配的快速圓弧檢測算法略小。所提算法的召回率在三種算法中始終最低，證明該算法的檢測精度最高。

(3)檢測效率對比。

為檢驗所提圓弧檢測算法的檢測效率，測試相同實驗次數下不同算法的檢測耗時，結果如圖7所示。

圖7 不同圓弧檢測算法檢測耗時對比

分析圖7可知，隨著實驗次數的不斷增加，不同圓弧檢測算法的檢測耗時也相應發生變化。基于邊界聚類的圓弧檢測算法的檢測耗時僅在最初時少于所提的基于多層卷積網絡的圓弧快速檢測算法，而基于切線段匹配的快速圓弧檢測算法的檢測耗時始終大于文中算法。對比結果表明，文中算法所用的檢測時間最少。通過上述實驗可知，所提圓弧檢測算法的檢測精度最高，因此可證明所提算法具有較高的檢測效率。

3 結束語

基于多層卷積網絡的圓弧快速檢測算法通過圓弧信息聚類存儲、圓弧全局聚類與獲取圓弧閾值區間實現了圓弧快速檢測，其檢測速度高于傳統圓弧檢測算法，并且誤檢率遠低于傳統圓弧檢測算法，實現了圓弧檢測領域速度與效率的提升，對圓弧檢測領域具有重大的意義。