一種基于標準差的K-medoids聚類算法
鄧玉芳,張繼福
(太原科技大學 計算機科學與技術學院,山西 太原 030024)
0 引 言
聚類分析是數據挖掘[1]、模式識別[2]等領域的重要研究內容之一,在識別數據的內在結構方面具有重要的作用[3],并已廣泛地應用在金融分析、疾病診斷、假新聞檢測[4]、農業災害預測等實際問題中。聚類分析是一種常用的無監督數據挖掘方法[5],可將數據集劃分成若干個簇,目標是使在同一個簇里的數據相似度盡可能得高,不同的簇之間的數據相似度盡可能得低,由此根據數據信息將數據劃分為若干簇,揭示數據的原始分布。K-medoids算法[6]是一類基于劃分的聚類分析方法,具有對孤立點敏感度低和良好的魯棒性等優點,并已得到了廣泛應用。
目前,大多數K-medoids聚類算法,由于初始聚類中心點的選取和中心點迭代更新等原因,存在著聚類精度和效率較低,且需要額外設置參數等不足。文中利用標準差選擇候選初始聚類中心,給出了一種K-medoids聚類分析算法。該算法首先利用標準差定義了初始中心點候選集度量公式,有效地避免密集程度較低的樣本點,尤其是孤立點作為初始聚類中心;其次采用從兩個初始中心點逐步增加中心點直到K個中心點的方式,從初始中心點候選集中確定初始中心點,避免初始中心點選擇在同一個聚類簇;然后按照將數據樣本歸屬于最近的中心點的原則,形成初始聚類簇;再次更新聚類中心點,直到與上一次的聚類誤差平方和相同,形成聚類簇;最后采用UCI數據集和人工數據集進行實驗,驗證了該聚類算法的有效性。
1 相關工作
聚類分析是將數據集劃分成若干個簇,在簇里的數據對象的相似度盡可能高,不同簇之間的數據對象的相似度盡可能低。常用的聚類分析算法大致分為:基于劃分的方法、基于密度的方法、基于層次的方法、基于網格的方法、基于模型的方法[7],以及基于子空間的方法[8-10]。K-medoids算法由于是以簇中心的實際樣本對象作為簇中心點,從而有效地降低了對于噪聲數據和孤立點的敏感性。K-medoids聚類算法在選擇初始中心點時,有可能選為離散點或異常點,容易使聚類過程陷入局部極值,同時也需要不斷地迭代更新聚類中心點,因此聚類效果和效率較差。
K-medoids聚類算法經典的PAM算法思想是:選取數據集中實際樣本對象來代表類簇中心,首先隨機選擇K個初始中心點,將剩余的所有非中心點樣本分配到與其最為相似的聚類簇中,計算聚類代價函數。其次選取一個非中心點樣本作為新的中心點替換原來的中心點,然后計算替換中心點后的聚類代價函數,如果聚類代價函數減少,則由新的中心點替換原來的中心點,形成新的K個中心點,按此方式不斷地進行中心點的迭代更新,直到聚類代價函數不再降低,沒有可以替換的中心點為止。目前K-medoids聚類分析的研究成果主要集中在如下三方面。
(1)初始聚類中心點選取。
Park等人提出了快速K-medoids算法[11],按照密度排序,采用前K個樣本點作為初始中心點。在更新中心點時采用了K-means,相比PAM算法在計算量上有所降低,在效率上有所提高。但是因為采用的選取初始中心點的方式會導致選取的初始中心點可能在一個聚類簇,因此不能很好地選擇出分布在不同簇的初始中心點,使得聚類效果的準確性不高。馬箐等人提出了基于粒計算的K-medoids聚類算法,采用了粒度概念[12],該聚類算法給出了新的樣本相似度函數,并定義了類簇中心,利用等價關系產生粒子,然后依據粒子包含樣本的數據量大小來定義粒子密度,最后選擇密度較大的前K個粒子的中心樣本點作為K-medoids聚類算法的初始聚類中心,改進K-medoids聚類算法的初始中心隨機選取對聚類結果的影響,從而提高K-medoids聚類算法的效率。謝娟英等人[13]提出了密度峰值優化初始中心的K-medoids聚類算法,該聚類算法首先需要做出決策圖,然后根據決策圖來確定初始中心點,但是同樣也會出現初始中心點選擇在同一個簇的情況。Yu等人[14]提出了INCK聚類算法,該聚類算法從部分符合要求的數據樣本中確定聚類中心,提高了聚類結果的準確性,但是在找尋符合要求的樣本時存在參數的選取問題,而參數的選取會影響聚類結果的準確性。為此,文中定義了新的初始中心點候選集,在原始數據上進行聚類。
(2)迭代更新聚類中心點。
Chu等人[15]推導了一個新的不等式,該不等式可用于最近鄰搜索問題。提出了基于新不等式,先前的中心點指標,內存利用,三角形不等式準則和部分距離搜索的四種基于K-medoids算法的搜索策略。顏宏文等人[16]提出了基于寬度優先搜索的K-medoids聚類算法。該算法利用粒計算初始化獲取K個有效粒子,從粒子中選出K個中心點作為初始中心點。之后分別對K個粒子中的對象建立以中心點為根節點的相似對象二叉樹,通過寬度優先搜索遍歷二叉樹迭代出最優中心點。宋紅海等人[17]提出了基于優化粒計算下微粒子動態搜索的K-medoids聚類算法。該算法是在優化的粒計算前提下,提出了基于微粒子動態搜索策略,以初始中心點作為基點,形成一個微粒子,在微粒子內部,采用離中心點先近后遠的原則進行搜索,有效地縮小搜索范圍,提高了聚類準確率。余冬華等人[18]提出的SPAM算法中在總結的三角不等式的基礎上提出了2個加速定理,其中一個定理適用于一次交換一個中心點的情況,另一個加速定理是第一個定理的擴展,可適用于一次交換多個中心點的情況。同時SPAM算法存儲樣本到其聚類中心的距離和中心點之間的距離,以提高效率。
(3)聚類分析的并行化。
在處理海量數據信息時面臨的內存容量和CPU處理速度的問題上通常采用并行化來處理。Jiang等人[19]實現了基于Hadoop分布式計算平臺上的K-medoids聚類。每個提交的作業都有許多迭代的MapReduce程序,在Map階段每個樣本被分到距離中心最相似的那個簇。在comebine階段計算每個簇的中心點,在reduce階段計算新的中心點。當新中心點和原來的中心點相同時停止迭代。Zhao等人[20]通過引入Canopy算法和Max-Min距離算法改進了原始的K-Medoids算法,并選擇了K個點作為聚類的初始中心。然后使用MapReduce計算框架來并行化算法,改進的聚類算法不僅具有良好的加速性能,而且提高了聚類的準確性和收斂性,在處理大規模數據方面具有很大的性能優勢。賴向陽等人提出了一種MapReduce架構下基于遺傳算法的K-Medoids聚類[21]。利用遺傳算法的種群進化特點來改進K-Medoids算法的初始中心敏感的問題,然后將遺傳K-Medoids算法再結合MapReduce并行,提高算法效率。王永貴等人提出了一種基于Hadoop的高效K-Medoids并行算法[22]。該算法通過改進初始中心點選擇和中心點替換策略這兩個方面提高聚類精度。利用Hadoop計算平臺結合基于Top K的并行隨機抽樣策略,實現了高效穩定的K-Medoids并行算法,之后又通過調整Hadoop平臺,實現了算法的進一步優化。
綜上所述,近些年來很多研究者都對聚類分析做了一定的研究。K-medoids算法作為一種基于劃分的聚類分析方法,以實際樣本點作為簇中心點,從而有效地降低了對于噪聲數據和孤立點的敏感性,具有良好的魯棒性。但是在選擇初始中心點時,有可能選為離散點或異常點,使得聚類準確性不高。迭代更新中心點需要大量距離計算,使得聚類效率較低。
2 基本概念
聚類分析任務是將給定數據集劃分成多個簇,使簇中的數據對象盡可能相似,不同的簇之間的數據對象差異性大,可采用歐氏距離來衡量數據對象之間的相似性[23]。假設數據集X={x1,x2,…,xn},樣本數為n,每個樣本的維數是p,第i個樣本的第a個屬性值表示為xia。參照文獻[13]兩個樣本間的歐氏距離,給出樣本xi與xj之間的歐氏距離,公式如下:
(1)
其中,d(xi,xj)表示樣本xi與xj的距離,i=1,2,…,n,j=1,2,…,n。
參照文獻[14],聚類誤差平方和、數據集的標準差和每個樣本的標準差公式分別定義如下:
(2)
其中,oi表示第i個簇的簇中心點,ci表示第i個簇,而x是屬于第i個簇的樣本點。數據集的標準差定義如下:
(3)
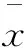
每個樣本的標準差公式如下:
(4)
其中,vi就是每個樣本的標準差值。
3 基于標準差的K-medoids聚類分析
3.1 初始中心點候選集
K-medoids聚類算法中初始中心點的選取影響最終的聚類結果。初始中心點選擇在接近最終聚類中心點區域時,聚類結果的準確性相對較高且迭代更新中心點的次數較少。當初始中心點選擇為嚴重偏離最終聚類中心區域的樣本或者孤立點時,聚類過程容易陷入局部極值,聚類結果準確性較低且迭代更新中心點的次數較多。在K-medoids聚類算法中,初始中心點選擇已成為提高聚類分析效果和效率的關鍵因素。
標準差在概率統計中最常使用統計分布程度上的測量,標準差定義為方差的算術平方根,反映數據的離散程度。標準差越小,反映數據分布比較密集,標準差越大,反映數據分布比較離散。聚類中心點的密集程度是較高的,所以中心點樣本的標準差相對是較小的。相反的孤立點樣本的密集度是較低的,孤立點樣本的標準差相對是較大的。對于上一章節給定的數據集X,依據式(3)和式(4),將每個樣本xi的標準差vi與整體數據集的標準差v進行比較,當vi小于v時,表明xi在分布密集程度相對較高的區域,因而成為聚類中心點的可能性要大;當vi大于v,表明xi在分布密集程度相對較低的區域,因而成為初始中心點的可能性要低。但是不能排除當vi略大于v時,樣本xi是中心點的可能性,所以以大于v的所有樣本的平均標準差作為初始中心點候選集的上界。從而既可以使密集程度較大的樣本點在初始中心點候選集內,又可以使離散程度不太大的樣本點也在初始中心點候選集里。
為了避免孤立點或者密集度較低的樣本點被選為初始中心點,同時也為了使初始中心點被選為密集度較大的樣本點,定義了初始中心點候選集,以進一步提高聚類的效果和效率。當樣本的標準差小于超出數據集標準差的所有樣本的平均標準差時,該樣本點就有可能是初始中心點,初始中心點候選集sm的定義如下:
sm={xi|vi≤v',i=1,2,…,n}
(5)
其中,v'是vi大于v的所有vi的均值。
在K-medoids聚類分析中,不必從全部數據對象中選擇初始中心點,僅從初始中心點候選集中選擇即可,從而有效地提高了聚類中心點選取效率和效果。
3.2 聚類分析
在K-medoids聚類算法中,初始中心點選擇尤為重要。在初始中心點的選取上,為了避免選取到孤立點作為初始中心點,同時又為了選取到密集程度較大的樣本點作為初始中心點,文中利用式(5)定義的初始中心點候選集,從初始中心點候選集選取初始中心點,并迭代更新,其聚類過程參考INCK聚類算法由如下兩步來實現。
首先在初始中心點候選集中選取兩個初始中心點,并迭代更新兩個初始中心點。在選擇第一個初始中心點o1時,選取距離到所有樣本點距離之和最小的樣本點作為中心點,公式如下:
(6)
其中,樣本xi到所有樣本點的距離之和di的公式如下:
(7)
第二個初始中心點o2的選取為初始中心點候選集中距離第一個初始中心點最遠的樣本點,使初始中心點盡可能地選擇在不同的聚類簇中,避免出現在同一聚類簇里,公式如下:
(8)
然后按照就近原則聚類,把所有的樣本點歸屬于距離最近的中心點,計算聚類誤差平方和,之后更新每個簇中心,使每個簇內新中心點距離其簇中所有樣本的距離之和最小,公式如下:
(9)
其中,cj表示第j個聚類簇,xl要和xi一樣是屬于cj,如果xl不屬于cj,則不將其與xi的距離算在內。用新中心點代替原中心點,然后聚類計算聚類誤差平方和,若與上一次聚類誤差平方和一樣則不再更新中心點,否則繼續更新中心點。
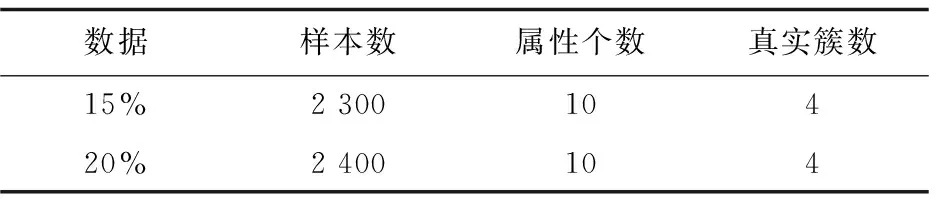
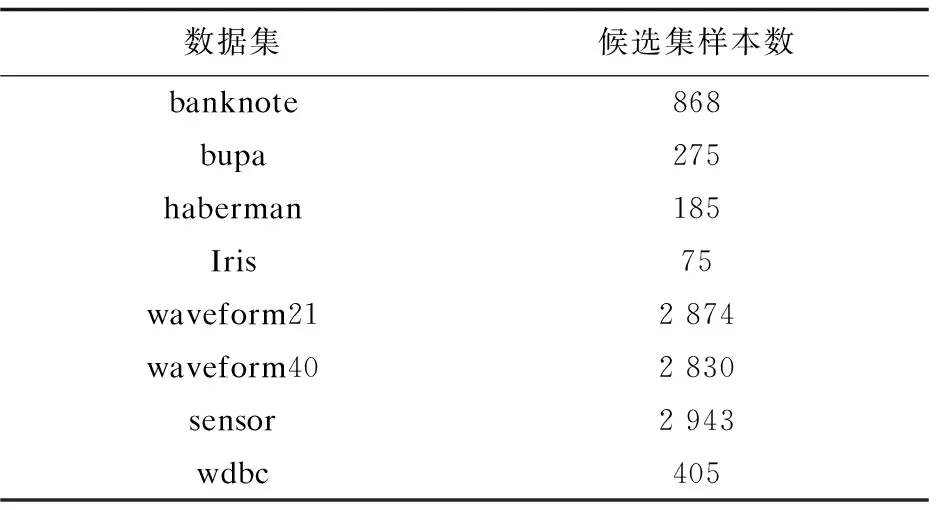
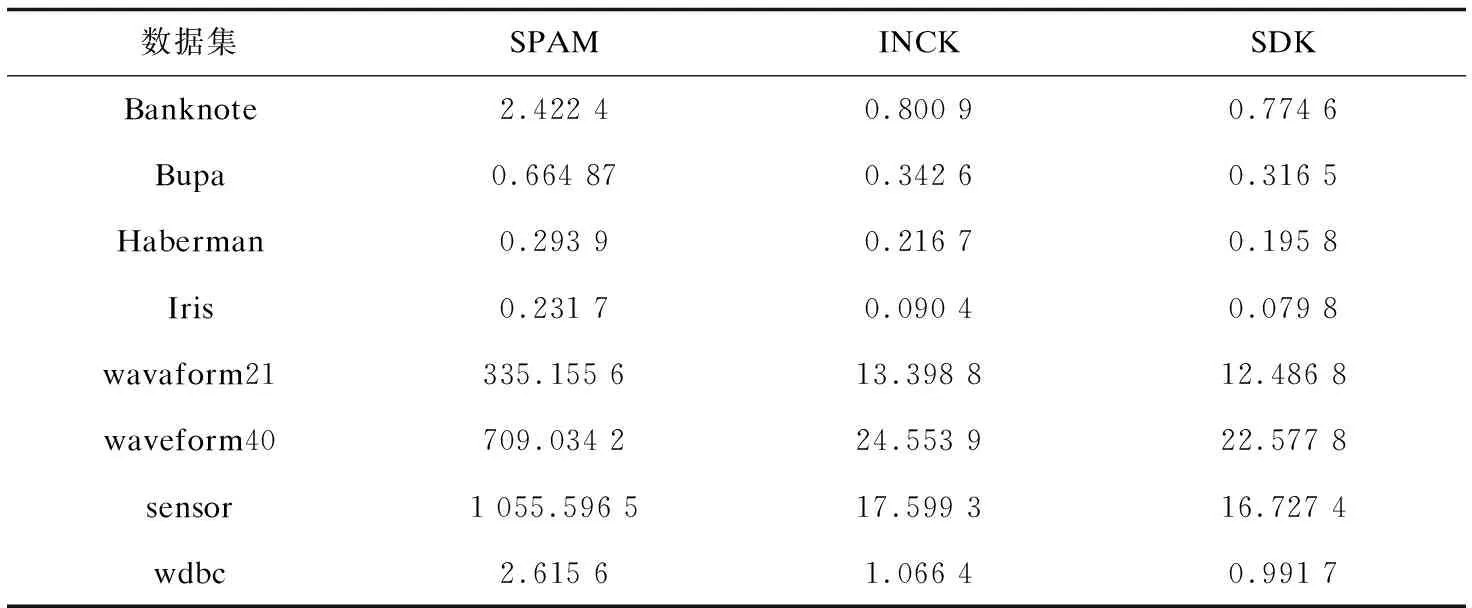
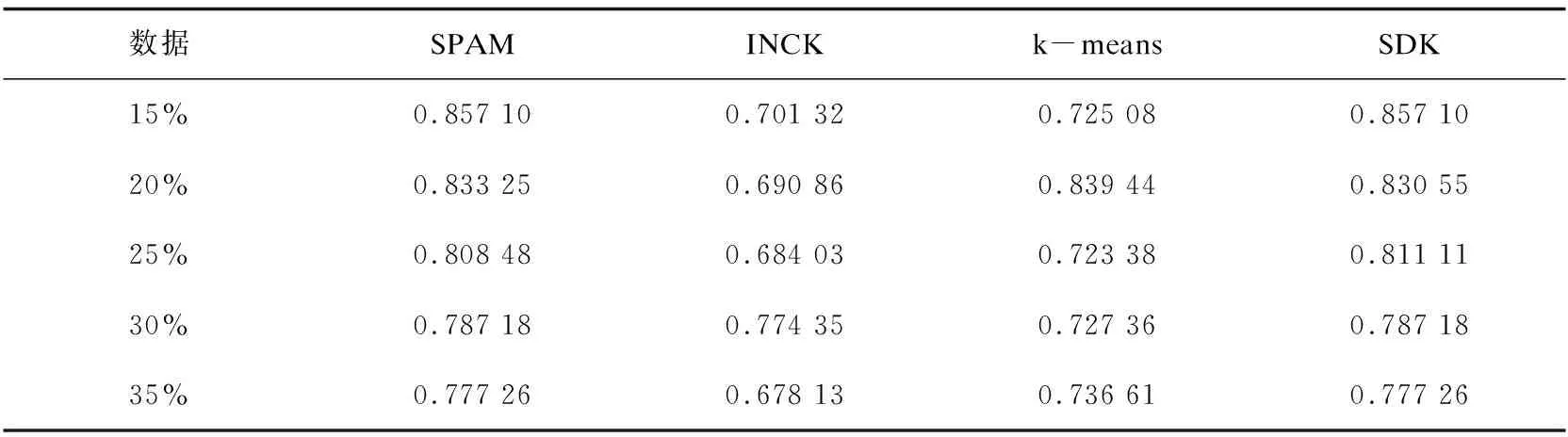
其次從初始中心點候選集中,選取其余的k-2個初始中心點。假設已經得到g(2≤g (10) (11) 然后聚類迭代更新中心點。按此方式逐步增加初始中心點直到確定k個中心點,并得到最終聚類結果。 根據上一小節聚類分析的基本思想,基于標準差的K-medoids聚類分析算法偽代碼描述如下所示。 算法1:SDK聚類算法(standard-deviation-based K-medoids clustering algorithm) 輸入:數據集X,簇數k 輸出:k個聚類簇 (1)sm=getsm() (2)fori=1 tondo (3) forj=1 tondo (4)根據式(7)得到di (5) end for (6)end for (7)fori=1 tosdo (8)根據式(6)得到第一個初始中心點o1,s為初始中心點候選集大小 (9)end for (10)fori=1 tosdo (11)根據式(8)得到第二個初始中心點o2 (12)end for (13)Cluster() (14)fori=1 tondo (15)按照式(2)計算聚類誤差平方和E (16)end for (17)Update(); (18)ifk>2 then (19) forg=2 tok-1 do (20) forj=1 tosdo (21)根據式(10)和式(11)得到第g+1個初始中心點 (22) end for (23) Cluster(); (24) forh=1 tondo (25)按照式(2)計算聚類誤差平方和E (26) end for (27) Update(); (28) end for (29)end if 算法2:getsm() 輸入:數據集X 輸出:初始中心點候選集sm (1)fori=1 tondo (2) forj=itondo (3)計算得到樣本間距離d(xi,xj) (4) end for (5)end for (6)fori=1 topdo (7) forj=1 tondo (9) end for (10)end for (11)fori=1 tondo (12)根據式(3)得到數據集標準差v (13)end for (14)fori=1 tondo (15) forj=1 tondo (16)根據式(4)得到每個樣本點的標準差值vi (17) end for (18)end for (19)fori=1 tondo (20)根據式(5)得到sm; (21)end for 算法3:Update() 輸入:g個中心點 輸出:更新后的g個中心點和g個聚類簇 (1)While true do (2) fori=1 tondo (3) forj=1 tondo (4)按照式(9)找到更新后的中心點 (5) end for (6) end for (7) Cluster(); (8) forh=1 tondo (9)按照式(2)計算聚類誤差平方和newE (10) end for (11) if newE==E then (12) break; (13) else (14) E=newE (15) end if (16)end while 算法4:Cluster() 輸入:g個中心點 輸出:g個聚類簇 (1) fori=1 tondo (2)d=d(xi,o1) (3) setlabeli=1 (4) forj=2 tokdo (5) newd=d(xi,oj) (6) if newd (7) setlabeli=j (8)d=newd (9) end if (10) end for (11) end for 在SDK聚類算法中,由算法2計算樣本間距離的時間復雜度是o(n2),計算均值的時間復雜度是o(np),計算數據集的標準差的時間復雜度是o(n),計算所有樣本的標準差的時間復雜度是o(n2),計算初始中心點候選集的時間復雜度是o(n),在算法1中計算di的時間復雜度是o(n2),選取初始中心點的時間復雜度是o(ks)。在算法4中,樣本聚類的時間復雜度為o(nk),因此整體的聚類時間復雜度是o(nk2),在算法3中,假設更新中心點的最大迭代次數是t次,則更新中心點的時間復雜度是o(tn2),所以整體的更新中心點的時間復雜度為o(tkn2),因此SDK聚類算法的整體的時間復雜度是o(n2+np+n+n2+n+n2+ks+nk2+tkn2),最終時間復雜度表示為o(n2+tkn2+nk2)。 實驗環境:Intel(R) Core(TM) i5-8265U CPU,8 G內存,windows10操作系統,eclipse作為開發平臺,采用java語言實現SDK聚類算法。文中為驗證SDK聚類算法的準確性以及魯棒性,選用SPAM聚類算法,INCK聚類算法和經典的聚類算法k-means[24]在UCI數據集和人工數據集上進行實驗驗證。在對準確性的驗證上采用了Rand指數還有F-measure值這兩個評價指標。在驗證SDK聚類算法的聚類效率時,與同樣是K-medoids聚類算法的SPAM聚類算法、INCK聚類算法進行實驗對比。在實驗中SDK聚類算法、SPAM聚類算法以及經典k-means聚類算法的參數只需要k值,INCK聚類算法除了需要設定參數k值外,還需要一個額外的參數λ。 文中在實驗中采用了UCI數據集,用來分析比較不同聚類算法的準確性和效率。在實驗中采用的所有數據集的名稱,數據的樣本數,樣本屬性個數和真實的簇數如表1所示,其中sensor表示的是sensor_readings_24數據集。同時為了實驗分析聚類算法的魯棒性,采用了Matlab工具,隨機生成了5組符合正態分布的人工數據集。在每組數據集分為4類,每類有500個數據樣本,屬性維度是10維的基礎上,分別增加15%、20%、25%、30%、35%的噪聲數據,從而形成5組人工數據集。表2為生成人工數據集的各種具體參數。按照表2給出的參數,隨機生成了5組人工數據集,生成的5組人工數據集的具體的樣本數,屬性個數以及真實的簇數如表3所示。 表1 UCI數據集 表2 生成人工數據集的參數 表3 人工數據集 續表3 在SDK聚類算法中,由于采用了初始中心點候選集,所以聚類初始中心點選擇不必從全部的數據樣本中去確定,并且更為準確且有效。在實驗驗證中各個數據集的初始中心點候選集的樣本個數如表4所示。 表4 初始中心點候選集 由表4可以看出,在實驗中采用的所有數據集的初始中心點候選集樣本數相較于原來整體數據集都減少了,從而在確定初始中心點時,不必從全體數據中尋找,減少了計算量,有效地提高了聚類效率。 為了驗證SDK聚類算法的聚類效果,實驗采用SDK聚類算法與SPAM聚類算法和INCK聚類算法以及k-means聚類算法在UCI數據集上進行了聚類精度的實驗對比,其中實驗結果數據采用了各算法運行10次的平均值。 從圖1和圖2的結果可以看出,無論是Rand指數還是F-measure值,表現最好的是SDK聚類算法,因此整體上,聚類的準確性最高的是SDK聚類算法。SDK聚類算法的聚類準確性相對較好主要是因為在對初始中心點的選取上,避免了選取孤立點為初始中心點,同時又盡可能地避免選取的初始中心點在同一個簇的情況,并且使初始中心點選在密集度相對較高的樣本上,因而聚類準確性上表現較好。 圖1 真實數據集上Rand指數的值 圖2 真實數據集上F-measure的值 采用表1所示的UCI數據集,與同樣是K-medoids算法的SPAM聚類算法和INCK聚類算法進行實驗對比,驗證SDK聚類算法的效率。實驗結果如表5所示,其中取10次運行結果的平均值作為實驗結果。 由表5可知,SDK聚類算法效率是最高的,而SPAM聚類算法效率是最差的,INCK聚類算法的效率居中。其主要原因是SDK聚類算法采用了初始中心點候選集的方式,確定中心點的時候不必從全部樣本中選擇,在更新中心點時和INCK聚類算法一樣采用了快速K-medoids的方式,而SPAM聚類算法采用的是PAM聚類算法的中心點更新方式,從全部數據樣本中查找中心點,所以SDK聚類算法在計算量上相對減少。除此之外,SDK聚類算法和INCK聚類算法采用了存儲樣本之間距離的方式,之后用到直接調用即可。SPAM聚類算法雖然也采用存儲距離的方式,但是只存儲樣本點到其中心點的距離和中心點之間的距離,在之后用到其他兩個樣本之間的距離時都要重新計算。因此SDK聚類算法和INCK聚類算法都減少了不必要的距離的重復計算,而SPAM聚類算法需要重復計算距離。所以整體上SDK聚類算法和INCK聚類算法的效率都要比SPAM聚類算法要高,而文中SDK聚類算法的效率是最高的。 表5 聚類算法運行時間 s 為了驗證SDK聚類算法的魯棒性,采用表3所示的人工數據集,將SDK聚類算法,SPAM聚類算法,INCK聚類算法和k-means聚類算法進行了實驗對比分析,其中實驗結果選取了各算法運行10次結果的平均值。表6是Rand指數的實驗結果,表7是F-measure的實驗結果。 表6 人工數據集上的Rand指數 表7 人工數據集上的F-measure 從表6和表7可知,在4個聚類算法中,SDK聚類算法和SPAM聚類算法的魯棒性表現相近且表現較好,INCK聚類算法的魯棒性是最差的。SDK聚類算法的魯棒性保持良好的主要原因是SDK聚類算法采用了初始中心點候選集,在選取中心點的時候,盡量避免不合適的數據被選為中心點。 利用了標準差反映數據分布離散程度的原理,定義了初始中心點候選集,從初始中心點候選集中選取初始中心點,避免孤立點或者密集度較低的樣本點被選為初始中心點,同時也使初始中心點選為密集度較大的樣本點。在UCI數據集及人工數據集上進行了實驗驗證,其實驗結果驗證了該算法的有效性。下一步的工作主要是對SDK聚類算法的并行化。
3.3 聚類分析算法
3.4 時間復雜度分析
4 實驗結果及相關分析
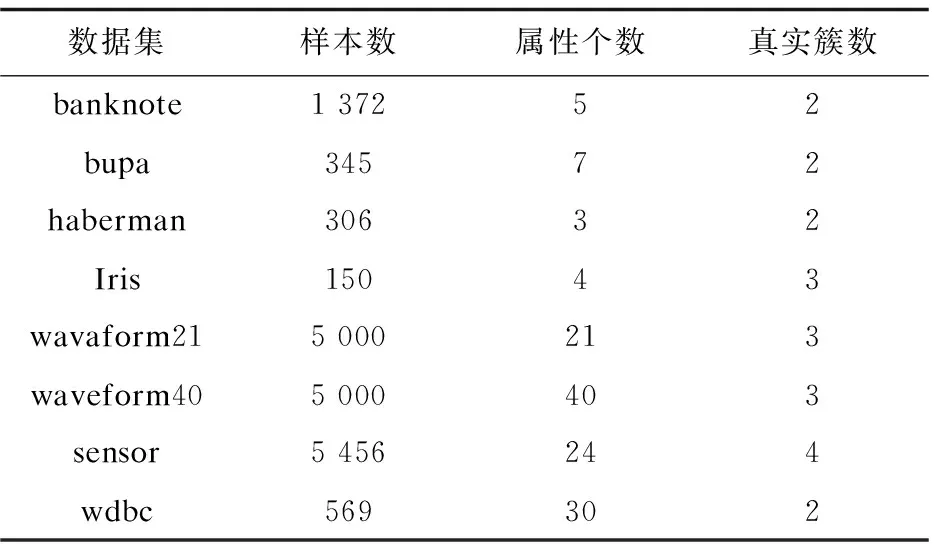
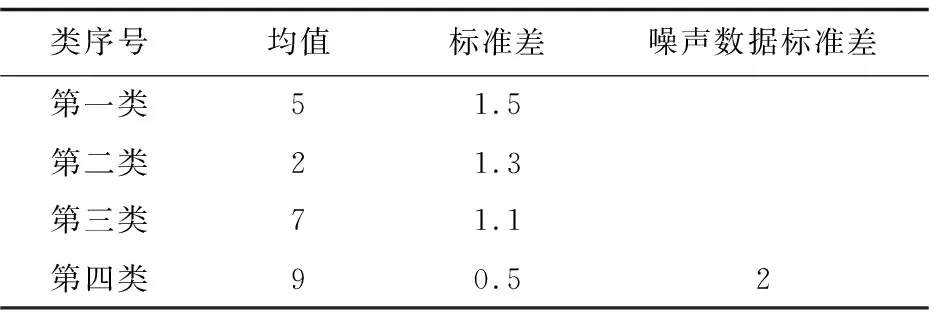
4.1 數據集

4.2 初始中心點候選集
4.3 聚類精度


4.4 聚類效率
4.5 聚類魯棒性

5 結束語

