卡箍動力學特性研究

呂金華，臧朝平，許本勝, 2，劉忠華，張讓威

(1. 南京航空航天大學 能源與動力學院，江蘇 南京 210016； 2. 桂林航天工業學院 機械工程學院，廣西 桂林 541004)3. 中國航空工業集團 沈陽發動機設計研究所，遼寧 沈陽 110000)

0 引言

航空發動機外部管路主要用于輸送燃油、滑油和空氣等介質，是發動機附件系統的重要組成部分。在航空發動機的使用過程中外部管路常發生斷裂、漏油等故障，振動是管路斷裂的主要原因和誘導因素[1]。卡箍是在航空發動機外部管路中起增強管路剛度、緊固管路位置的重要零件，卡箍對管路系統振動特性具有重要影響[2]。

馮凱等人利用有限元法分析了不同數量、位置的卡箍對管路固有頻率的影響，并以此為依據進行了管路調頻[3]。劉偉等人將卡箍視為末端固定的平移約束彈簧單元，討論了卡箍數量和剛度對管路系統動力學特性的影響[4]。KWONG A H M等人采用遺傳算法對管路卡箍布局進行了優化，并用試驗驗證了其理論的可靠性[5]。目前的研究多集中于卡箍布局對管路特性的影響，而忽視了對卡箍自身動力學特性的研究。

本文首先對卡箍直管系統在不同擰緊力矩下進行模型試驗，研究擰緊力矩對卡箍剛度的影響；其次對卡箍處于不同位置的直管系統進行試驗和仿真研究，驗證本文得到的卡箍剛度與擰緊力矩的函數關系，對管路系統設計具有重要的指導意義。

1 基于測試數據辨識卡箍剛度及相關性分析

基于模態試驗數據辨識卡箍剛度的流程如圖1所示。對卡箍直管系統進行模態試驗，利用試驗數據對卡箍直管系統有限元模型中的剛度參數進行修正，使有限元模型的分析結果與試驗結果的誤差滿足要求，獲得可以反映實際卡箍動力學特性的剛度參數。對卡箍直管系統在不同擰緊力矩下進行模態試驗，利用試驗數據辨識卡箍在不同擰緊力矩下的剛度參數，得到卡箍剛度與擰緊力矩的函數關系。

圖1 基于測試數據辨識卡箍剛度流程

相關性分析的主要目的是分析有限元模型和實際結構之間的誤差程度，以判斷是否需要對有限元模型進行修正。如果有限元模型與實際結構之間的相關性較差，說明有限元模型無法準確反映實際結構的動力學特性，需要對模型進行修正。常用的相關性分析評判標準有頻差，模態置信準則為MAC。

頻差為有限元模型的仿真固有頻率與實際結構對應的試驗頻率之間的差異，表達式為：

(1)

其中：fi為有限元模型的第i階仿真頻率;fit為實際結構的第i階固有頻率。

工程上，模態置信準則(MAC)被廣泛應用為模態振型的相關程度。MAC值公式為：

(2)

MAC值的取值范圍為0～1，一般認為，MAC值超過0.6可以認為兩階振型是相關的，MAC值低于0.2，則可認為兩階振型是不相關的。

2 擰緊力矩對卡箍剛度影響

2.1 卡箍直管系統在不同擰緊力矩下的模態試驗

本文研究的卡箍直管系統如圖2所示。直管為不銹鋼管，長400 mm，外徑為9.5 mm，內徑為7.5 mm。直管左端伸進夾具40 mm，卡箍距離直管右端40 mm，卡箍擰緊力矩為1 Nm。整個實驗在鑄鐵平臺上完成，最大程度地降低了環境的影響。

圖2 卡箍直管系統

卡箍直管系統模態試驗如圖3所示。由于卡箍結構的不對稱性，分別在水平、豎直兩個方向對卡箍直管系統進行模態試驗。在直管表面從固支處每隔40 mm布置1個測點，共布置10個測點。在1號測點左邊附近激勵，用多普勒激光測振儀逐個采集各個測點的速度響應數據[6-7]。通過水平、豎直兩個方向的模態試驗，可以得到卡箍直管系統在1 Nm擰緊力矩下的前3階模態頻率和模態振型，分別如圖4和表1所示。卡箍直管系統1、3階振型為水平彎曲，2階振型為豎直彎曲。

圖3 卡箍直管系統模態試驗

圖4 卡箍直管系統前3階模態振型

在2～7 Nm范圍內，以1 Nm為步長，共取6個擰緊力矩值，分別作為圖3中卡箍的擰緊力矩，重復上述試驗，得到卡箍直管系統分別在1～7 Nm擰緊力矩下的前3階模態頻率，如表1所示。

表1 卡箍直管系統在1～7 Nm擰緊力矩下的前3階頻率

各階頻率隨著擰緊力矩的增大而增大，且都在6 Nm處趨于穩定。比較卡箍直管系統分別在1 Nm和7 Nm擰緊力矩下的各階頻率，1階提高了4.31%，2階提高了4.98%，3階提高了5.38%。這說明擰緊力矩對卡箍的剛度具有明顯的影響。

2.2 卡箍直管系統的建模

卡箍直管系統有限元模型示意圖如圖5所示。直管由40個梁單元組成，單元截面為同心圓，內徑為7.5 mm，外徑為9.5 mm。梁單元材料參數如表2所示。考慮到直管的加工誤差，根據直管的實際質量，對直管的密度進行了修正。

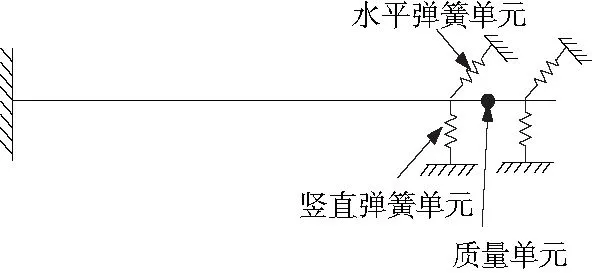
圖5 卡箍直管系統示意圖

表2 梁單元材料參數

由2.1節試驗可知，卡箍直管系統1、2階振型相似，方向不同，但是頻率相差較大，這說明卡箍的水平剛度與豎直剛度相差較大。因此，本文建立水平彈簧單元和豎直彈簧單元以分別考慮卡箍的水平剛度、豎直剛度。卡箍對管路的實際約束接近于固支約束，但是僅在卡箍中間位置建立一個水平彈簧單元和豎直彈簧單元無法限制管路的轉動自由度。因此本文在卡箍的左右兩側各建立一個水平彈簧單元和豎直彈簧單元來模擬卡箍對管路的實際約束。同時在卡箍的中間位置建立一個質量單元以考慮卡箍的質量。為了簡化分析，認為卡箍左右兩側同方向上的彈簧單元參數一致，如表3所示。

表3 卡箍簡化模型中的單元參數

在直管左端施加固支約束，對卡箍直管系統有限元模型進行模態分析，得到前3階模態頻率如表4所示。與卡箍直管系統在各個擰緊力矩下的試驗結果對比如表5所示。1階模態的最小頻差為-6.49%，2階模態的最小頻差為4.22%，3階模態的最小頻差為-31.59%。這說明有限元模型中的卡箍剛度參數無法反映實際卡箍在各個擰緊力矩下的剛度特性，需要對其進行修正。

表4 卡箍直管系統模態分析結果

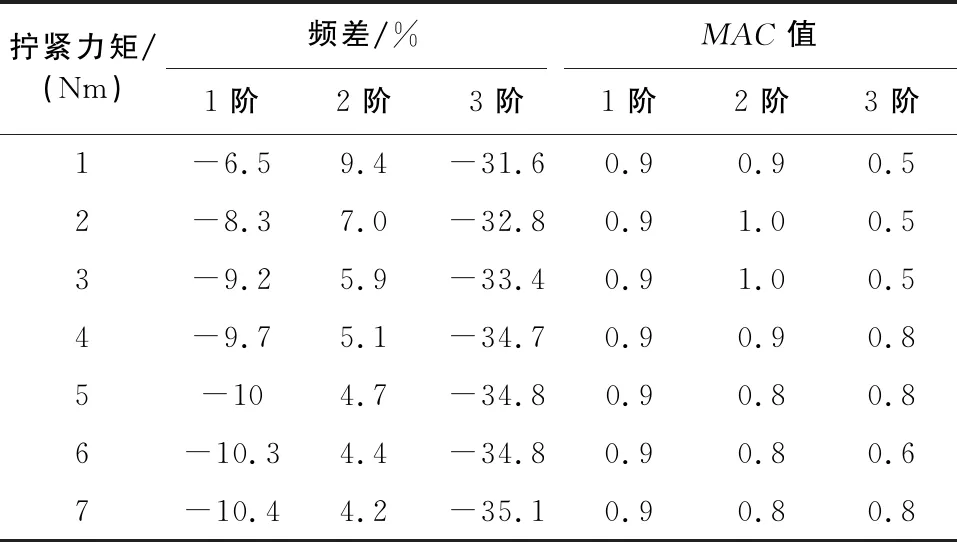
表5 卡箍直管系統模態分析結果與試驗結果對比

2.3 模型修正

以卡箍直管系統的試驗頻率作為修正目標，對卡箍直管系統有限元模型中卡箍的水平、豎直剛度進行修正，辨識卡箍在各個擰緊力矩下的水平、豎直剛度，如表6所示。

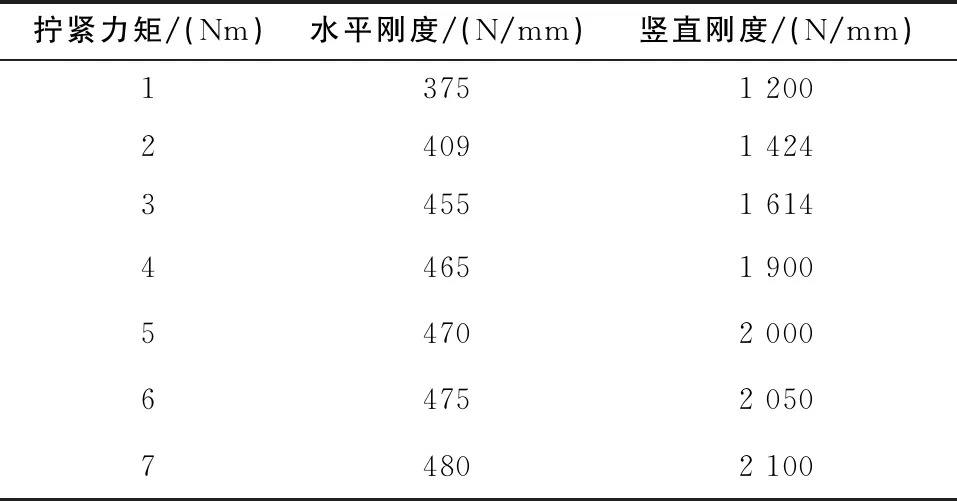
表6 卡箍在不同擰緊力矩下的剛度參數

修正后卡箍直管系統在各個擰緊力矩下的模態分析結果與試驗結果對比如表7所示。

表7 修正后卡箍直管系統的模態分析結果與試驗結果對比

修正后卡箍直管系統有限元模型在各個擰緊力矩下的模態分析結果與試驗結果的最大頻差為4.87%。除了1～3 Nm擰緊力矩下的第3階模態振型的MAC值較低，其余MAC值都在0.8以上，這說明修正后的卡箍剛度參數可以反映實際卡箍在各個擰緊力矩下的剛度特性。

通過表6可以得到卡箍水平、豎直剛度與擰緊力矩的函數關系，分別如式(3)、式(4)所示。

(3)

(4)

式中：kshuiping為卡箍水平剛度；kshuzhi為卡箍豎直剛度；M為擰緊力矩。

3 卡箍位置對管路系統特性影響

3.1 卡箍位置對管路系統特性影響的試驗研究

分別將圖2中卡箍向左平移到距離管路右端80 mm、120 mm、160 mm、200 mm、240 mm、280 mm的位置，重復卡箍直管系統在不同擰緊力矩下的模態試驗，得到將卡箍置于不同位置處直管系統在不同擰緊力矩下的水平、豎直基頻，從而建立簡單直管系統水平、豎直基頻與卡箍位置關系曲線，如圖6所示(本刊系黑白印刷，有疑問之處可咨詢作者)。

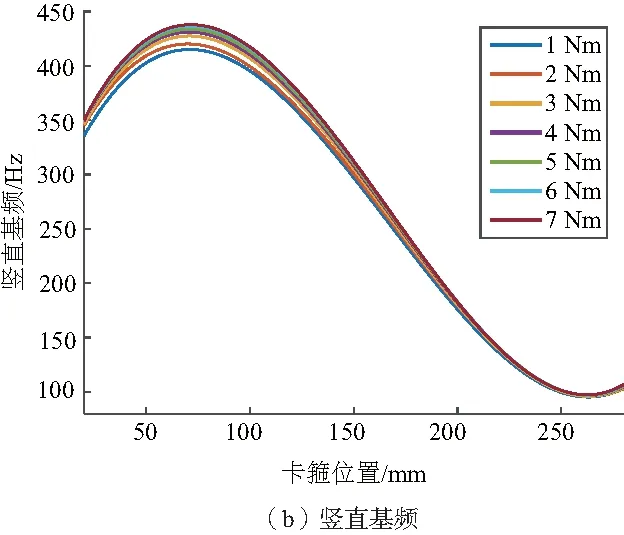
圖6 卡箍直管系統水平、豎直基頻與卡箍位置的關系

隨著卡箍向左端固支處接近，卡箍直管系統在不同擰緊力矩下的水平、豎直方向的基頻都是先增大后減小。當卡箍距離直管右端64.1 mm時，直管系統在各個擰緊力矩下的水平基頻達到最大；當卡箍距離直管右端69.5 mm時，直管系統在各個擰緊力矩下的豎直基頻達到最大。

3.2 卡箍位置對管路系統特性影響的仿真研究

基于2.3節得到的卡箍水平剛度、豎直剛度與擰緊力矩的關系，仿真不同卡箍位置的管路系統在不同擰緊力矩下的模態實驗，得到不同卡箍位置的管路系統在不同擰緊力矩下的前2階仿真頻率，與試驗結果對比如表8所示。

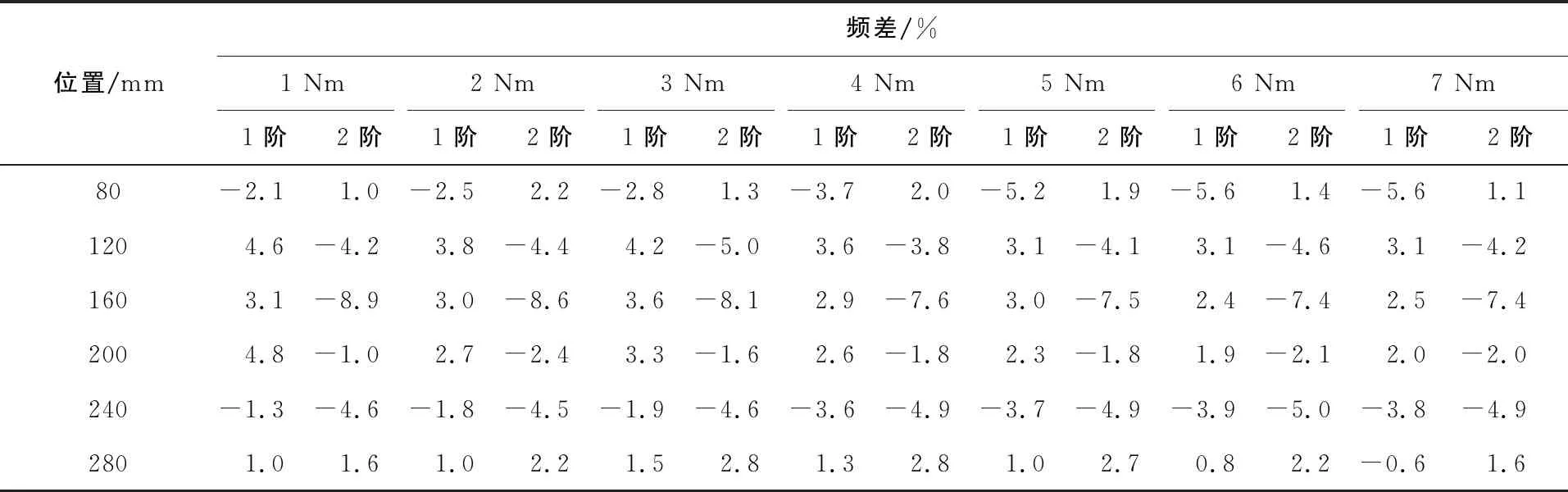
表8 不同卡箍位置管路系統在1～7 Nm擰緊力矩下的前2階仿真頻率與試驗頻率對比

水平方向基頻的最大誤差為-5.6%，豎直方向基頻最大誤差為-8.92%，絕對值都在10%以內，且絕大多數頻差的絕對值都在5%以內。這說明2.3節得到的卡箍水平剛度、豎直剛度與擰緊力矩的函數在直管任何位置都適用。

4 結語

本文通過卡箍直管系統在不同擰緊力矩下的模態試驗，建立了卡箍水平、豎直剛度與擰緊力矩的函數，并通過卡箍位置對管路系統特性影響的試驗與仿真研究，驗證了本文建立的卡箍水平、豎直剛度函數在直管任何位置都適用。本文的研究對管路系統的設計具有重要的指導意義，但是必須指出的是，本文結果建立在簡單直管系統研究的基礎之上，如果要推廣到復雜管路系統，還需要做進一步研究。