基于斑馬帶的轉子系統軸系扭振測量技術

嚴丹丹，岳林

(南京航空航天大學 機電學院，江蘇 南京 210001)

0 引言

轉子軸系是一個結構復雜的彈性連續體，很容易受到周期性變化轉矩的影響而產生扭轉振動。扭轉振動會使軸產生劇烈的應力變化，并會因金屬疲勞現象產生裂紋，嚴重的情況下甚至會由于轉子斷裂導致相關設備損壞。因此應當特別關注轉子軸系的扭轉振動現象；同時，當扭轉振動頻率與軸系的固有頻率相近引起共振時，會嚴重影響工件穩定性，甚至導致工件結構失效斷裂。對扭振的準確測量是診斷轉子系統故障的基礎。

扭振的測量方法分為接觸式測量和非接觸式測量兩種。由于接觸式測量方法需要在旋轉部件上安裝傳感器，傳感器的信號線需要通過滑環引出，測量系統的成本較高，且需要對原系統的結構進行一定的改進，通用性較差。而非接觸測量方法安裝簡單，通用性更強[1]。

扭振的非接觸測量通過測量轉子瞬時轉速的變化來求得扭振信息。瞬時轉速是扭轉振動實驗中的一個重要測量量，其精度直接影響扭轉振動實驗的測試精度[2-4]。瞬時轉速通過安裝在轉子上的齒輪、光電編碼器發出脈沖的時間間隔以及角度間隔計算得到，而由于在安裝、使用這些部件過程中產生的偏差和這些部件原始存在的系統偏差等，這些不可避免的因素必然會對后續扭振分析的精度造成影響。因此在進行扭振分析時，需要對其中一些影響扭振分析的常見因素進行分析和誤差校正，從而獲得較為準確的瞬時轉速值，以保證后續實驗的精確性[5-7]。本文主要采用斑馬帶進行扭振信號采集，其優點是安裝簡單，僅僅需要粘貼在轉子表面，因此適用場合廣泛。缺點是由于斑馬帶上黑白條紋的繪制精度不高，因此各條紋不能看做是等角度分布的，需要在測量之前事先通過算法標定每個條紋所對應的角度。本文對斑馬帶條紋的角度間隔進行測量和校正，并結合斑馬帶校正方法對扭振信號瞬時轉速計算原理進行改進，提出了一種軸系扭振過程中斑馬帶脈沖信號的仿真方法；通過仿真信號進行對上述扭振測量方法進行驗證。最后，通過扭振測量方法診斷了轉子系統的碰磨故障，證明了方法的有效性。

1 扭振測量技術原理

存在扭振的情況下，軸系的轉角由剛體旋轉和扭振兩部分構成，如式(1)。

φ(t)=ω0t+Asin(ωt+ψk)

(1)

式中：ω0t即為軸系的剛體旋轉引起的角度變化；ω0為被測軸的旋轉角速度；正弦分量為扭振角，A為扭振角振幅，ωt為扭振角頻率。

當扭轉振動中包含多個頻率分量的時候，式(1)可以寫作：

(2)

式中ωtk、ψk、Ak分別表示第k個振動分量的旋轉角速度、振幅和初始相位。

由式(2)可以得出，在進行扭轉角度計算時，需要對測得的軸瞬時角速度進行處理，即去掉軸的平均轉速ω0，再對其進行分析，即可得到軸的扭振信號。

1.1 瞬時角速度計算原理

每條斑馬帶通過激光傳感器時的上升沿實際到達時間為t(n)，無扭振情況下，上升沿的理論到達時間為tref(n)，兩者之間存在著一定的時間差，如圖1所示。對該時間差進行處理，即可得到軸系的扭振角速度和扭振角度(本刊黑白印刷，相關疑問咨詢作者)。

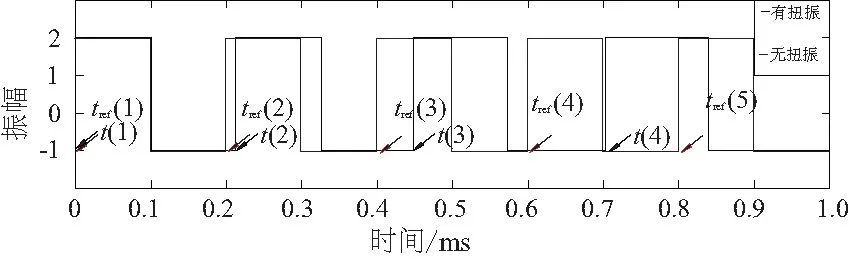
圖1 帶扭振和無扭振信號的對比

假設轉子系統上斑馬帶的數量為B，則轉軸旋轉第j圈的時間T為：

T(j)=t(B(j+1))-t(B·j)

(3)

其中經過第j圈中第b個條紋所對應的時間Δtj(b)為：

Δtj(b)=t(B·j+b+1)-t(B·j+b),1≤b≤B

(4)

經過第b個條紋時軸的瞬時轉速如式(5)所示。

(5)

其中r(b)代表每條斑馬帶在一圈中的占比，若斑馬帶條紋等分，則每條斑馬帶的占比為：

(6)

之后，對瞬時轉速進行數值積分即可得到轉子的扭振角度。

1.2 斑馬帶測量扭振的誤差及校正

在實際情況中，斑馬條紋分布是不均勻的，斑馬帶的誤差會對后續扭振計算過程中帶來誤差，因此需要對斑馬帶條紋寬度進行校正。

已知第j圈中第b個條紋的通過時間Δtj(b)以及軸系第j圈的通過時間T(j)，軸在勻速旋轉的前提下，兩者的比值近似于第b個條紋在一圈中的占比，如式(7)所示。

(7)

但由于扭振以及測量誤差的存在，rj(b)和真實的占比還存在著一定的差距，該差值在0上下浮動，因此通過平均可以使誤差相互抵消，使測量結果更加接近真實的占比，如式(8)所示。

(8)

2 仿真信號分析

2.1 斑馬帶脈沖信號仿真

帶有扭振的情況下，轉子在tn時刻的扭轉角度如式(9)所示。

(9)

式中：V0為起始轉頻；α為轉子的角加速度；tn為信號中的第n個采樣時刻；θ(tn)為由轉子扭振引起的轉角。

從最后一個上升沿的開始時刻到tn時刻，轉子轉過的角度γ(tn)為：

(10)

式中：R為每個條紋所占的角度，符號“?」”為取整符號，?x」表示一個小于或等于x的最大整數。

根據γ(tn)與R的比值，判斷傳感器在當前條紋中的位置：轉速脈沖的上升沿、高電平或者低電平。

(11)

脈沖仿真信號在上升沿、高電平段和低電平段分別滿足如下的函數：

(12)

2.2 不均勻斑馬帶校正

為驗證斑馬帶校正方法的準確性，根據2.1的信號仿真原理，生成一組斑馬帶不均勻的勻速脈沖信號，其仿真參數如表1所示。

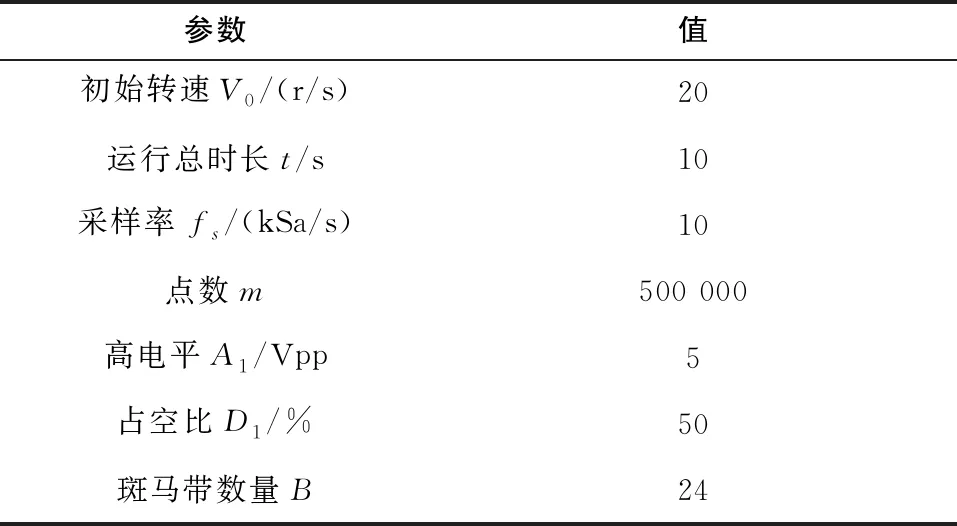
表1 勻速信號參數

仿真信號中的條紋數B=24，條紋的實際寬度占比在1/24上下隨機浮動，如圖2中的星號所示。根據1.2節中的方法求得的條紋占比如圖2中的圓圈所示。可以看出，計算所得的占比與仿真值相吻合，其相對誤差接近于0，說明本文采用的誤差校正方法是可行的。

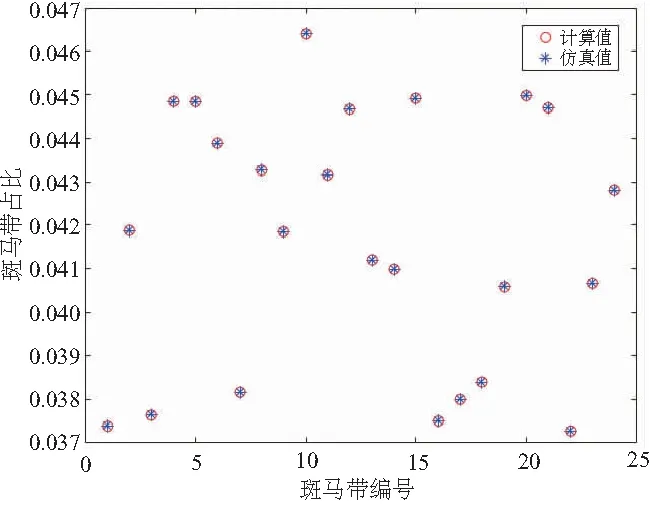
圖2 不均勻斑馬帶仿真校正

將不均勻斑馬帶占比植入仿真脈沖信號，采用前文中瞬時轉速和扭轉角度的計算方法，可得到考慮和不考慮斑馬帶補償情況下的瞬時轉速和扭轉角度，如圖3、圖4所示。可以看出，在不考慮斑馬帶不均勻性的情況下得到的瞬時轉速和扭轉角度有巨大的誤差，而采用了本文的條紋寬度校正方法后，求得的瞬時速度和扭轉角度和原始仿真值吻合得很好。

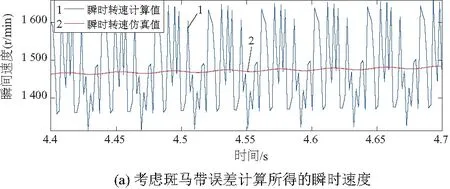
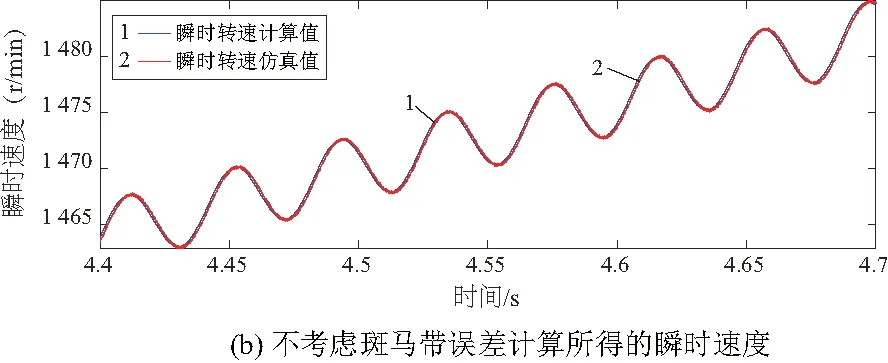
圖3 瞬時速度

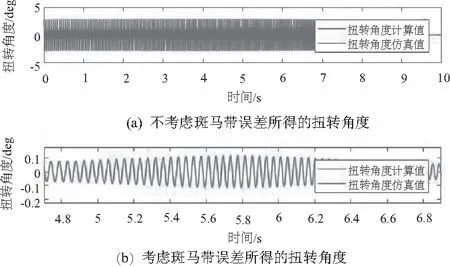
圖4 扭轉角度

3 實驗驗證

驗證本文方法的雙盤轉子系統實驗臺如圖5所示。CUT-2轉子實驗臺主要包括轉速調節器、電機、雙盤轉子系統、聯軸器、兩支激光轉速傳感器、兩個軸承座、底座以及斑馬帶等。斑馬帶上的黑白條紋寬度大致相等，且交替分布。斑馬帶附著在轉子圓柱面上，跟隨轉子同步扭振。1號激光轉速傳感器被放置在聯軸器附近，該傳感器一圈僅發出一個脈沖，作為參照信號，用于確定斑馬帶上各條紋的編號。2號激光轉速傳感器對準斑馬帶，用于計算扭振角速度和扭振角度。

圖5 扭振測量實驗系統

本次實驗采用的斑馬帶白色條紋數目為24，條紋寬度為10 mm。采用前文的方法對斑馬帶占比進行標定。標定時，利用轉速調節器將雙盤轉子系統的轉速控制在200 r/min低速勻速轉動，系統采樣率設置為102.4 k。標定結果的最大相對誤差<4%。

轉子在3 100r/min運行時的瞬時轉速如圖6所示。可以看出，由于180圈～320圈附近發生碰磨，瞬時轉速有明顯的變化，如圖7所示。通過對健康狀態下和碰磨狀態下260圈附近的瞬時轉速計算所得的扭轉角度進行階次分析，得到的階次譜圖如圖8和圖9所示。從圖中可以看出，在健康狀態下生成的1階譜幅值為0.248，而在碰磨情況下1階幅值為0.287，后5階幅值在碰磨狀態下相較于健康狀態的幅值都有所增大。由于兩次實驗的差別僅僅在于第2次實驗對CUT-2實驗臺用黃銅碰磨螺釘進行了碰磨，因此可認為扭轉角度階次譜幅值增大是碰磨的原因造成。

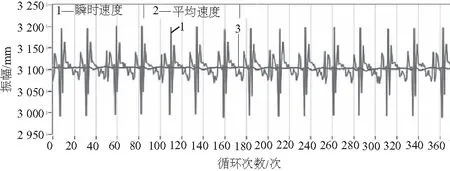
圖6 健康狀態下的瞬時轉速

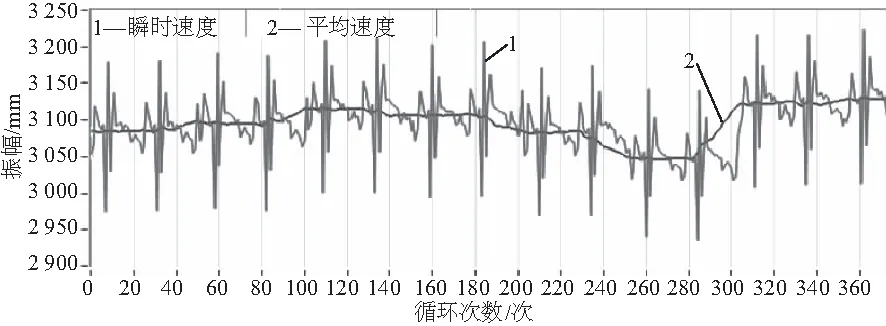
圖7 碰磨情況下的瞬時轉速

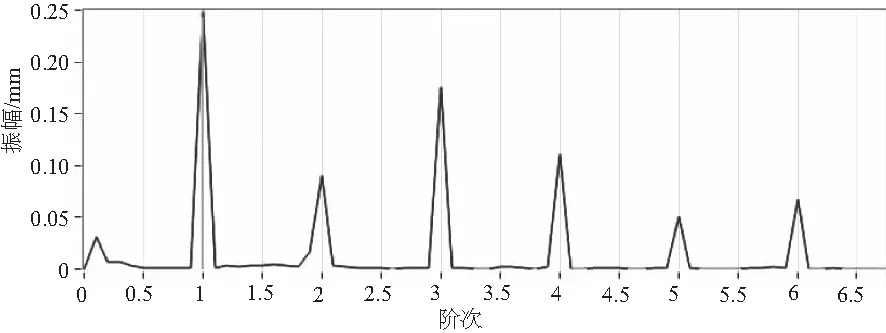
圖8 健康狀態下扭振角度的階次譜

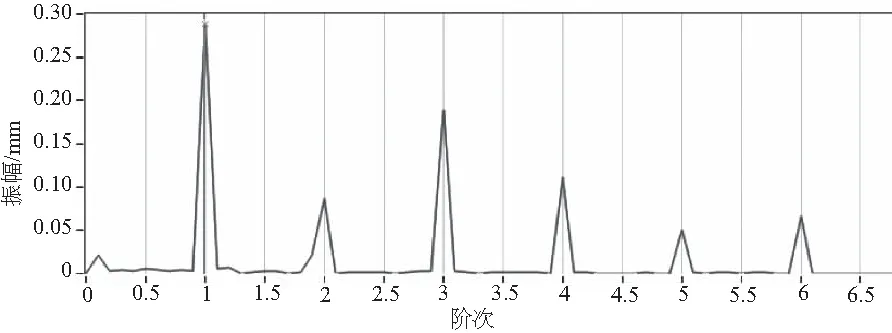
圖9 碰磨狀態下扭振角度的階次譜

4 結語

本文論述了基于斑馬帶進行扭振測量的技術難點，并采取了合理的解決方法。對利用斑馬帶進行信號采集過程中產生的誤差進行測量和校正。提出了一種扭振脈沖仿真信號的生成方法，結合斑馬帶校正方法對扭振信號瞬時轉速計算原理進行改進，并根據計算所得的瞬時角速度和扭轉角度進行分析。最后，通過一組轉子系統碰磨實驗驗證了方法的有效性。

主要結論如下：

1) 在采用斑馬帶補償改進的算法計算所得瞬時轉速和扭轉角度的精度得到極大的提高。

2) 采用斑馬帶補償改進的算法所得的扭振固有頻率的精度更高。

3) 碰磨發生后，轉子的扭振振幅出現了明顯的變化，可以據此識別出扭振故障。