R3上一類特殊Besicovitch集的維數估計
陳澤斌
(汕頭大學數學系,廣東 汕頭 515063)
1 引言
Kakeya在1917年提出了尋找單位直線段可以在其內部調轉方向并且具有最小面積的平面集的問題,也就是連續地移動此單位直線段而不離開此集使它旋轉180?并回到原來位置,這個問題基本上可歸結為尋找包含每個方向單位直線段的最小區域的問題.1928年,Besicovitch發現了一個平面上的單位直線段可以在其內部轉到相反方向,但其面積卻可以任意小的令人驚奇的集的構造.即有如下定理.
定理1.1有一個面積為零的平面集,它在所有方向上都包含一單位直線段.
上述定理的證明參考文獻[1].Rn中在每個方向包含有一個直線段的集合稱為Besicovitch集,定理1.1證明了R2中存在Besicovitch集;取這種集與Rn?2的乘積集,就得到了Rn上的Besicovitch集.隨著這個問題的解決,一個很自然的問題擺在眼前,就是如下著名的Kakeya猜想.
猜想Rn空間中的任意Besicovitch集的Hausdorff維數等于n.
關于Kakeya猜想,國際上已經有很多數學家(如Wolff,Bourgain,Tao等)做了大量的工作,其中n=2的情形已完全解決,并存在好幾種證明方法(見文獻[1–3]).而對于高維(n≥3)的情形,雖然目前還沒得到徹底解決,但是有許多著名的數學家做出了本質的推進.1985年,Christ-Duoandikoetxea-Rubio de Francia[4]首先證明了下界為.1991年,著名數學家Bourgain[3]利用一個稱為“bush”的構造將其改進為這里εn是一個固定的數,只與n有關.而這項工作最突出的結果來自于Wolff[5],1995年Wolff利用另一個稱為“hairbrush”的更有效的構造再次將這個下界提高至,其中對于3≤n≤8.這仍然是目前最好的結果.而對于n≥9,之后Katz–Tao[6]于2000年將其提高至.
由上述可知在高維空間Kakeya猜想雖然已得到豐富的結果,但是可以看到,即使是n=3的情形,最好的結果也僅是2.5,距離最終結果3還差了很多.針對n=3,利用已有的構造和方法要想進一步提高這個下界是相當困難的.那么一個比較自然的想法是,若僅對一類特殊的Besicovitch集進行維數估計,能否推出這類Besicovitch集的Hausdorff維數等于3呢?本文以此作為出發點.將Kakeya問題二維情形的一種證明方法(參考文獻[2])推廣到R3空間,接下來將定義一類圓盤型Besicovitch集,具體如下.
定義1.1令E為Rn中的圓盤型Besicovitch集,E包含以所有ξ∈Sn?2(n≥3)為法向量,點a為圓心的各個方向的單位圓盤,即E={x∈Rn:|(x?a)|≤1,(x?a)·ξ=0}.為方便起見,將這類型的Besicovitch集簡記為E集.下面是與之相關的δ-圓盤概念:
定義1.2令0<δ?1,對E中任一方向的圓盤,給其增加δ厚度,使其成為一個δ-圓盤,記為即這里x⊥=x?(x·ξ)·ξ.
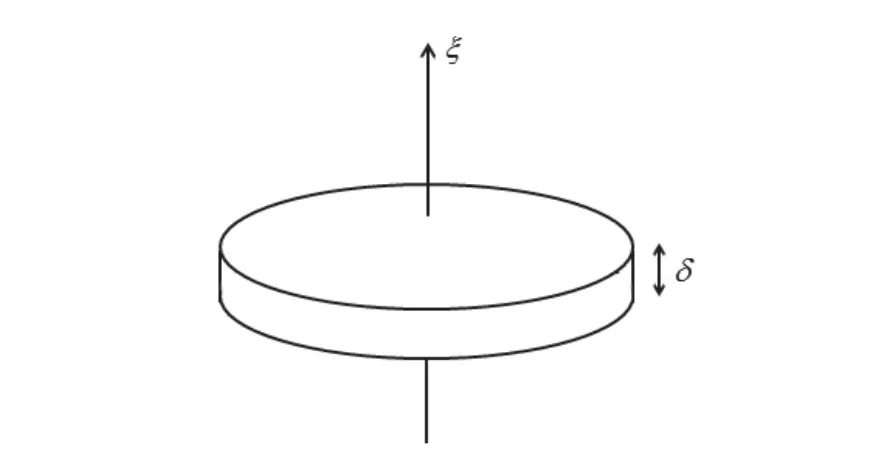
圖1:δ-圓盤
2 主要結論
回顧了Kakeya猜想的研究背景和研究現狀,針對上面定義的圓盤型Besicovitch集,本文的主要結論如下.
定理2.1R3上的E集的Hausdorff維數為3.
3 預備知識
在這一節,將介紹Hausdorff維數和δ-分隔子集的概念,并做一些符號的約定.
定義3.1令E∈Rn,α>0,對0<δ≤1,定義這里κδ是E的可數覆蓋,由半徑ri<δ的小球B(xi,ri)構成的集合,即
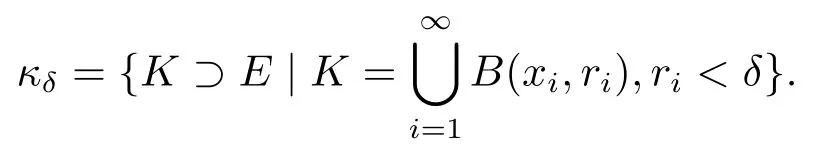
令δ→0,得到E的α-Hausdorff測度
對任意E∈Rn,為α的非增函數.一步,若α<β,則從而若Hβ(E)>0,則Hα(E)>0為無窮.因而存在唯一的數,記為dimHE,稱為E的Hausdorff維數,滿足若0≤α 定義3.2令E∈Rn,S?E,若任意不同的兩點x,y∈S滿足|x?y|≥δ,那么稱S為E的δ-分隔子集. 為了方便敘述,做如下約定 (1)表示集合A中元素的個數; (2)對于f和g兩個函數,fg表示存在常數C,獨立于f和g,使得f≤Cg. 所以 故 結合定理4.1和定理4.2,即得定理2.1. 本文在R3空間定義了一類圓盤型Besicovitch集并對其進行維數估計,證明了該圓盤型Besicovitc集的Hausdorff維數為3.因為Kakeya二維情形已有的證明方法無法推廣到高維空間上,所以接下來將會致力于尋找高維情形新的證明方法.4 定理2.1的證明


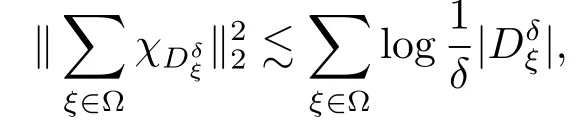
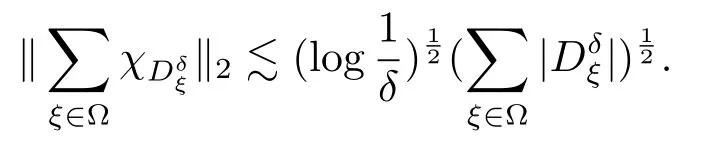
5 結論
- 數學雜志的其它文章
- 完整Coriolis力與弱地形作用下的非齊次mKdV-Burgers方程
- 有窮平坦維數的同調轉換刻畫
- 正合范疇的整體Gorenstein維數
- S3中等參曲面的兩個特征
- FEKETE-SZEG PROBLEMS FOR SEVERAL QUASI-SUBORDINATION SUBCLASSES OF ANALYTIC AND BI-UNIVALENT FUNCTIONS ASSOCIATED WITH THE DZIOK-SRIVASTAVA OPERATOR
- NONCONFORMING FINITE ELEMENT METHOD FOR THE NONLINEAR KLEIN-GORDON EQUATION WITH MOVING GRIDS

