不同網格加筋殼承載能力比較及影響因素研究

董曼紅，胡正根，劉觀日，李 斌，阮小鵬

（北京宇航系統工程研究所，北京，100076）

0 引 言

貯箱作為貯存燃料的部段，同時又承受軸向載荷，在火箭設計中起到至關重要的作用。貯箱由前短殼、前底、筒段、后底和后短殼組成，前底、筒段和后底焊接成一個封閉的容器用來貯存燃料，與前后短殼焊接，再通過前后短殼與相鄰部段連接[1]。

本文對正置正交網格及等邊三角形網格加筋殼筒段在不同直徑和內壓的承載能力進行分析，得出工程計算方法以及計算結果分析。

1 不同網格加筋殼在運載火箭上的應用

因為火箭結構的特點和載荷方式，貯箱筒段會受到內壓、軸向力和彎矩的作用。在貯箱設計中，會對載荷進行綜合分析來確定貯箱筒段的設計載荷，以內壓作為設計載荷時，筒段會采用光筒結構形式；以軸壓為設計載荷，筒段會采用網格形式。

目前國外常用的網格形式主要有正置正交、斜置正交和正置等邊三角形網格等。20世紀70年代美國麥道宇航公司針對正置正交網格加筋殼結構的抗扭剛度低、斜置正交加筋殼結構的軸壓剛度低等缺點，率先提出了正置等邊三角形網格加筋殼結構，其后世界各國開始研究和應用正置等邊三角形加筋殼體，例如美國德爾它4、宇宙神5火箭，歐洲阿里安5和日本H2系列運載火箭貯箱均廣泛采用三角形網格加筋結構。目前，Φ5 m直徑及以下的國外普遍采用正置等邊三角形網格，Φ9 m級左右的網格加筋殼普遍采用正置正交網格加筋殼。

中國運載火箭設計中，以軸壓為設計載荷的筒段，傳統型號一般采用化銑的斜置正交結構，隨著技術的發展，在新型運載火箭設計中，為了提高結構承載效率，降低結構質量，火箭貯箱殼段網格加筋殼的選擇主要集中在正置正交網格殼和等邊三角形網格殼[1,2]。

為了給貯箱筒段設計提供正確的設計依據，需要對正置正交網格殼和等邊三角形網格殼進行計算方法的確認以及分析。貯箱及筒段結構如圖1、2所示。

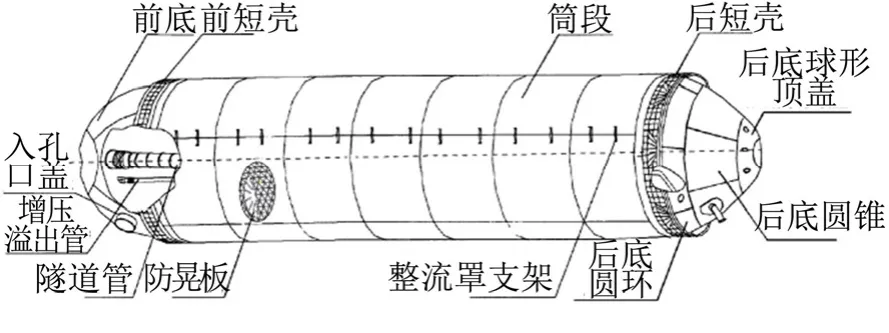
圖1 貯箱結構示意Fig.1 Tank Structure

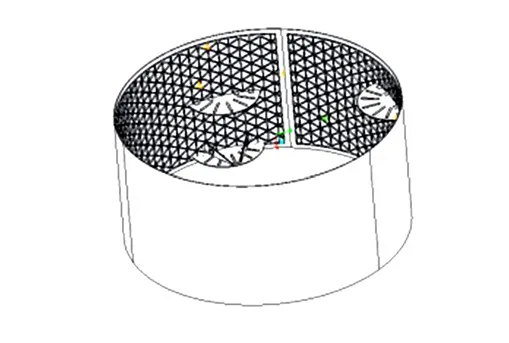
圖2 筒段結構示意Fig.2 Tube Structure

2 不同網格加筋殼承載能力計算方法

2.1 計算方法

等效剛度法（Equivalent Stiffness Method，ESM）是一種針對加筋筒殼結構的解析等效方法，是傳統的加筋筒殼結構抹平方法，對于加筋單胞構型復雜的情況難以實現準確解析公式，而且筋條只能承受軸向載荷的假設導致其分析結果誤差較大。針對軸內壓工況網格加筋筒殼，為了獲得高效率、高精度的承載能力工程計算方法，通過商業軟件實現的快速數值求解方法—漸近均勻化方法（Novel Numerical Imрlementation of Asymрtotic Homogenization Method, NIAH），在計算三維和二維周期性微結構的材料等效性質方面已經具有成熟的理論和算法，計算方法的有效性已被蔡園武和程耿東等人驗證[4]。本文采用漸近均勻化方法作為工程計算方法，對網格加筋殼筒段進行分析計算。這種計算方法針對于加筋筒殼結構，計算流程為：

a）從加筋筒殼中劃分出代表性單胞結構，建立其有限元模型；

b）基于漸近均勻化方法計算單胞結構的等效剛度系數Aij、Bij和Dij；

c）將上述等效剛度系數代入瑞利-里茲公式，計算得出整體型屈曲載荷值和屈曲模態波數。

傳統計算方法[5]計算A、B、D矩陣是簡化后的計算結果，而這種快速數值求解方法利用有限元強大的計算程序。把網格按照循環對稱劃分，只精確計算局部單胞的A、B、D矩陣，再代入工程計算，優點有：a）A、B、D矩陣精確；b）適合各種循環網格，可以把正置正交網格、豎三角形網格和橫三角形網格合成集合計算，同時可以計算筋條不等寬的網格加筋殼的承載能力。

2.2 快速數值求解方法精度驗證

2.2.1 算例驗證

以典型豎置三角網格加筋殼為例，驗證這種計算方法的精度。模型幾何參數如下：網格加筋殼直徑為Φ4000 mm，網格加筋殼高度L=6000 mm，蒙皮厚度ts=5.5 mm，壁板高度H=50 mm，筋條寬度tw=13 mm，筋條間距bs=135 mm。基于商用軟件AВAQUS建立網格加筋殼有限元模型，采用四節點殼體減縮積分單元S4R進行離散，蒙皮處的單元尺寸選為50 mm，筋條高度方向劃分兩個單元。設置簡支邊界條件，并基于子空間法計算線性屈曲載荷。有限元算法所得失穩波形如圖3所示，快速數值求解方法、線性有限元方法和等效剛度法的承載力計算結構的對比如表1所示。

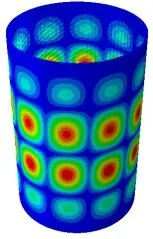
圖3 整體失穩示意Fig.3 Вucking Instability

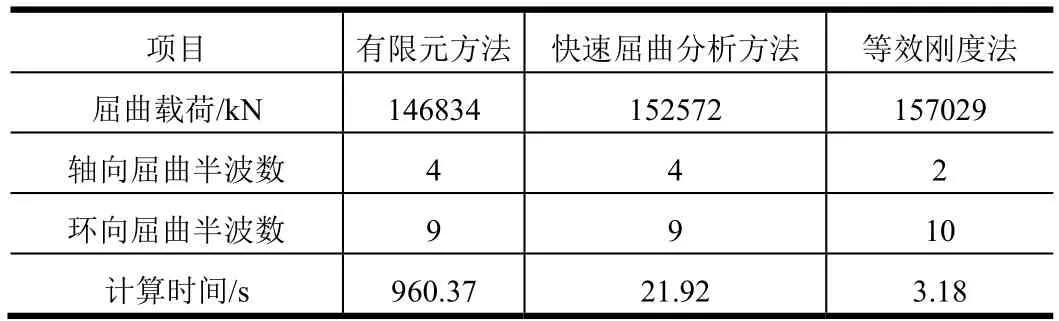
表1 失穩模式及計算時間對比Tab.1 Table of Instability Mode and Calculation Time

由表1可知，針對該模型，有限元法計算耗時960.37 s，得出的屈曲載荷為146 834 kN，環向半波數為9，縱向半波數為4；快速屈曲分析方法耗時21.92 s，計算得出的屈曲載荷為152 572 kN，其相較于有限元法的等效誤差為3.76%，環向半波數為9，縱向半波數為4；采用等效剛度分析方法耗時3.18 s，計算得出的屈曲載荷為157 029 kN，其相較于有限元法的等效誤差為6.94%，環向半波數為10，縱向半波數為2。

對比這 3種算法可知：快速數值求解方法相較于有限元方法，屈曲載荷計算結果僅差 3.76%（等效剛度分析方法等效誤差為 6.94%），計算效率提高了 44倍，同時捕捉到軸向屈曲半波數與環向屈曲半波數與有限元結果相同；快速數值求解方法相較于等效剛度法，計算精度更高，同時捕捉到的軸向屈曲半波數與環向屈曲半波數更精準。

快速數值求解方法與傳統的等效剛度法的等效剛度陣中的A陣基本一樣，B陣和D陣相差較大。這是因為傳統的等效剛度法對筋條進行等效，難以準確描述筋條與蒙皮之間的耦合關系。快速數值求解方法與傳統等效剛度法的A、B、D陣誤差分析如表2所示。

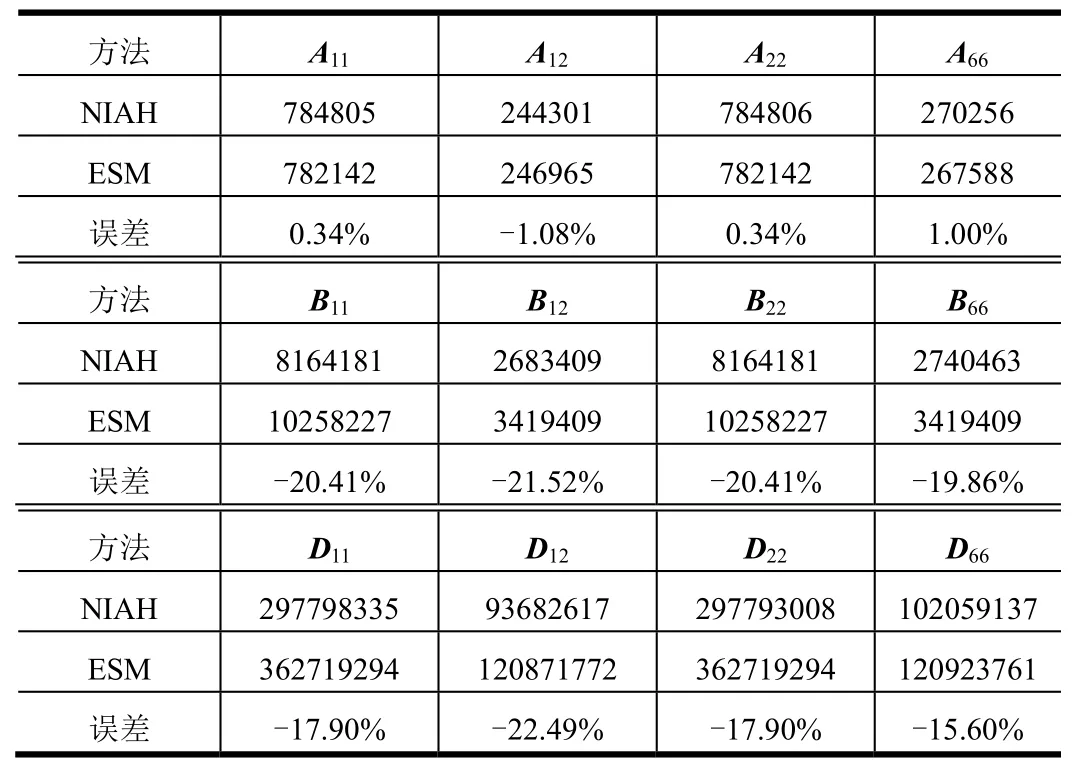
表2 快速數值求解方法與傳統等效剛度法的ABD陣誤差分析Tab.2 AВD Matrix Error of NIAH and ESM

2.2.2 樣本比較

針對數值模型的設計變量，抽取 100個采樣點計算，運用快速數值方法和等效剛度法對其進行計算，快速數值求解方法較有限元方法的相對誤差均在 10%以內，其中81個樣本點的相對誤差在5%以內；等效剛度法較有限元方法有94個樣本點的相對誤差在10%以內，有6個采樣點的相對誤差超過10%，最大誤差可達40.23%。說明快速數值求解方法更能準確地計算網格加筋殼的承載能力，可以用于新型運載火箭中貯箱筒段的設計。

3 不同網格加筋殼直徑和內壓對承載能力的影響

3.1 不同網格加筋殼算例確定

網格加筋殼優化條件為：a）彈性模量E=68 246 MPa，泊松比υ=0.33，屈服強度σs=363 MPa，極限強度σb=435 MPa，密度ρ=2.7×103kg/m3；b）載荷為純軸壓載荷；c）直徑為Φ9500 mm。

快速數值求解方法的優化目標：筒段長度12 000 mm，質量8000 kg左右，承載能力最大。有限元分析方法的優化目標：筒段長度12 000 mm，質量14 700 kg左右，承載能力最大。網格加筋殼的優化結果如表3、4所示，后文的計算結果均基于這組網格參數。

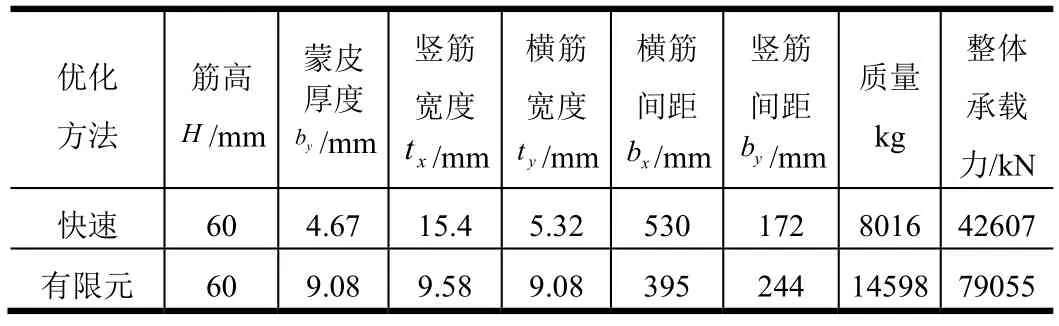
表3 正交正置網格優化結果Tab.3 Oрtimization Results of Orthogonal Mesh

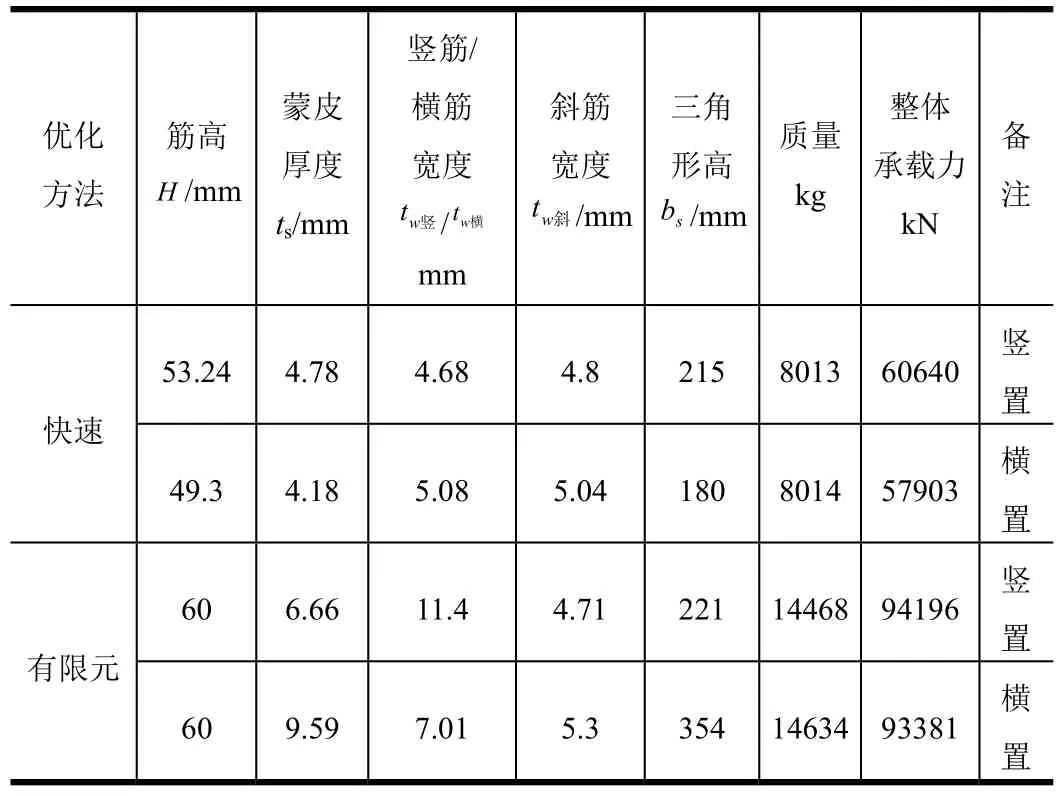
表4 等邊三角形網格優化結果Tab.4 Oрtimization Results of Eрuilateral Triangular Mesh

3.2 快速分析方法計算結果

正交正置網格筒段各個直徑筒段在網格參數相同的情況下，純軸壓作用下，承載能力相當，直徑關系不大；內壓對承載力有好處，內壓越大，承載能力越大，而且隨著直徑減小，內壓的好處隨著減小。

三角形網格筒段在純軸壓載荷作用下，豎置三角型網格筒段相對橫置三角形網格筒段有優勢，但是優勢不大；在網格參數相同的情況下，內壓和直徑對承載能力影響不大，與純軸壓承載能力相當。

3.3 有限元分析結果

a）模型說明。

貯箱包括前后底、筒段和前后短殼，筒段只是貯箱的一部分，為了準確模擬邊界條件，有限元模型由前后底、前后短殼和筒段組成。筒段作為關鍵模型，高度為12000 mm；前后短殼高500 mm，前后底為橢球結構，短殼和前后底給出足夠剛度，保證不先與筒段失穩，筒段材料為鋁合金2219。

b）模型邊界條件。

有限元模型為4節點殼單元（單元節點有3個平動自由度和3個轉角自由度），采用顯式動力學對筒殼結構進行非線性后屈曲分析。

軸壓作用時，約束下端面所有自由度和上端面除軸向外的其他5個自由度；內壓和軸壓作用時，約束下端面所有自由度和上短殼除軸向其他5個自由度，內壓和軸壓分兩個步驟施加：a）施加內壓，內壓初步取 0.1 MPa；b）以位移的形式施加軸壓，總位移為120 mm，根據軸壓時筒殼力位移曲線獲得網格加筋筒殼結構的極限承載力，從而計算得到承載效率。

c）結果分析。

正交正置網格筒段：在網格參數相同的情況下，純軸壓作用下，承載能力隨直徑的減小而減小；直徑不大于Φ3350 mm時，內壓對承載能力幾乎沒有影響；直徑大于Φ3350 mm時，承載能力隨內壓的增加先增加后減小，直徑不小于Φ7000 mm時，下降速度加快；快速分析方法計算中給的是整體失穩，所以失穩載荷幾乎不變，而有限元中給的是蒙皮筋條整體先失穩的載荷，隨直徑增加而增大，與前文分析一致。

三角形網格筒段，豎置和橫置變化趨勢一致：在網格參數相同的情況下，純軸壓作用下，承載能力隨直徑的減小而減小；當直徑不大于Φ3350 mm時，內壓對承載能力幾乎沒有影響；當直徑大于 Φ3350 mm時，承載能力隨內壓得增加而下降，當直徑不小于Φ7000 mm時，下降速度加快；三角形網格與正交正置網格筒段相比較，除正交正置網格筒段在直徑大于Φ3350 mm時隨著內壓增加有一段先升后降的趨勢外，其余變化趨勢一致，而這個內壓在0～0.3 MPa之間。

3.4 直徑和內壓對不同網格加筋殼承載能力的影響

3.4.1 純軸壓作用

工程計算結構承載能力與直徑關系不大，而有限元與直徑關系密切，這是因為：a）工程計算中計算結果是總體失穩載荷，而有限元計算的是整體失穩載荷、蒙皮失穩載荷、筋條失穩載荷的最小值。有限元模型Φ9500 mm直徑，對結構參數進行優化，整體先失穩，蒙皮和筋條后失穩，而隨著直徑的減小，網格參數沒有變化，導致蒙皮和筋條先失穩，這樣，隨著直徑的減小，承載能力減小；b）工程計算是線性計算，而有限元給的是非線性計算結果。

為此，選取正交正置網格筒段進行各個直徑下的承載能力計算：a）利用快速分析方法計算整體失穩載荷、蒙皮失穩載荷、筋條失穩載荷。在網格參數不變的情況下，整體失穩載荷隨直徑變化不大，而蒙皮和筋條失穩載荷隨直徑的減小而減小。取最小承載能力后，結果與有限元結果趨勢一致。b）對相同網格參數進行有限元的線性計算，當直徑大于Φ6000 mm時，工程方法與線性有限元法的結果基本相同；當直徑在Φ3350～5000 mm之間，計算結果相差10%以內；當直徑小于Φ3350 mm時，相差較大。這是因為各個直徑下，筒殼長一致保持12 m，直徑過小會導致結構由中長殼變為長殼而使結果不夠準確，這個問題可以通過更改模型長度解決。c）結果進一步證明，快速分析方法應用于初步設計是合理的，大直徑加筋殼筒段更適合這種快速分析方法。

3.4.2 軸壓和內壓聯合作用

正置正交網格網格加筋殼筒段快速數值求解方法計算結果是：內壓對軸壓承載能力有好處，直徑越大，好處越大；有限元計算當直徑小于等于Φ3350 mm時，內壓對承載能力幾乎沒有影響，直徑大于Φ3350 mm時，承載能力隨內壓的增加先增加后減小；在小內壓大直徑時，工程計算和有限元計算結果變化趨勢一致。

三角形網格加筋殼筒段，豎置和橫置三角形網格變化趨勢一致。快速分析方法計算結果是：內壓和直徑對承載能力影響不大，與純軸壓承載能力相當；有限元分析結果是當直徑小于等于Φ3350 mm時，內壓對承載能力幾乎沒有影響，當直徑大于Φ3350 mm時，承載能力隨內壓得增加而下降，當直徑大于等于Φ7000 mm 時，下降速度加快；也就是說，在小直徑時，工程計算和有限元計算結果變化趨勢一致。

為了比較兩種計算方法計算結果，確保計算結果正確。對Φ9500 mm直徑下的正置正交網格加筋殼筒段進行線性有限元計算，并與快速數值求解方法進行比較，如圖4所示。

圖4 正置正交網格快速分析方法和線性有限元計算結果對比Fig.4 Load-bearing Ability of Orthogonal Grid NIAH and Linear Finite Element

由圖4可知，有限元線性計算結果與工程計算結果變化一致。因為在純軸壓下結構已發生塑性失穩，隨著內壓增加，內壓帶來的初始應力越大，快速分析方法只能考慮線性屈曲，無法識別非線性塑性失穩，導致兩種方法對規律總結不一致。因此建議采用快速數值求解方法確認結構初步網格參數，根據各工況設計載荷進行非線性有限元計算復核結構承載能力。

3.5 扭矩對不同網格加筋殼承載能力的影響

正置正交網格及等邊三角形網格加筋殼承載力隨扭矩的變化如圖5所示。在扭矩逐漸增大的過程中，加筋筒的承載力都在減小；正置正交網格承載能力直線下降，等邊三角形網格加筋殼筋殼在小于 20 kN·m時，下降緩慢。因此，在扭距小于20 kN·m時，推薦采用三角形網格加筋殼設計。

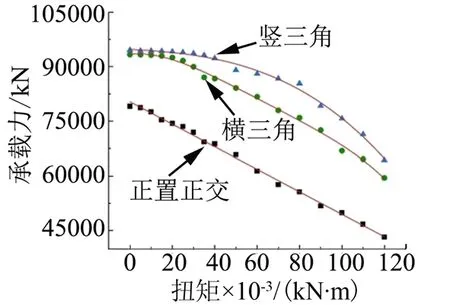
圖5 網格加筋筒承載力隨扭矩的影響Fig.5 Load-bearing Ability of Grid Reinforced Shell with Rejection

3.6 不同網格加筋殼承載能力比較

網格參數是在純軸壓Φ9500 mm直徑下進行優化的，因此，對Φ9500 mm直徑3種網格的承載能力進行數值分析。快速數值求解方法計算結果和有限元計算結果都表明：純軸壓作用下，三角形網格加筋承載力優于正置正交網格加筋筒，其中豎置等邊三角形網格加筋殼承載效率稍優于橫置等邊三角網格加筋筒的承載效率。但根據有限元計算，正置正交網格加筋殼在小內壓作用下，承載能力會有較小的增加，而等邊三角形網格加筋殼承載能力下降，因此，小內壓作用下，正置正交網格及等邊三角形網格加筋殼承載能力的大小，還需要根據具體載荷進行進一步的確認。

4 結 論

為了對大直徑貯箱筒段工程計算方法進行確認分析，本文對正置正交網格及等邊三角形網格加筋殼筒段計算結果進行分析研究，分析了直徑和內壓對網格筒段承載能力的影響：a）直徑小于等于Φ3350 mm，工程計算采用線性計算：正置正交網格內壓對承載能力有好處，但變化趨勢緩慢，非線性有限元計算結果內壓增加承載能力變化不大；豎直和橫置等邊三角形網格工程計算和非線性有限元計算結果都是內壓增加承載能力變化不大。b）直徑大于Φ3350 mm，工程計算采用線性計算，正置正交網格內壓對承載能力有好處，但變化趨勢緩慢，三角形網格幾乎不變；而非線性有限元計算中隨著內壓的增加，正置正交網格先升后降，三角形網格則下降。進而說明，通常認為的內壓對承載能力有好處是存在一定的條件的。c）正置正交網格及等邊三角形網格加筋殼承載力隨扭矩的增加而減小，但等邊三角形網格加筋在扭距小于 20 kN·m時下降趨勢緩慢，因此在扭距較小時，推薦采用等邊三角形網格加筋殼設計。