整流罩頭部鈍度比對運載火箭氣動性能影響研究

閆指江，吳彥森，宮宇昆，張耘隆，秦 曈

（北京宇航系統工程研究所，北京，100076）

0 引 言

近些年，中國的火箭設計及制造技術飛速發展，特別是以CZ-6、CZ-7和CZ-5為代表的新型運載火箭相繼成功首飛和應用發射，使中國運載火箭綜合能力進入國際先進行列[1]。而火箭的外形設計是其中的重要組成部分，直接影響了火箭的彈道特性、結構靜動力特性以及火箭的飛行穩定性等[2]。而外形設計中整流罩的外形設計是其中的關鍵環節，不但直接影響了內部的有效載荷尺寸，而且還決定了全箭的氣動特性及相應的氣動熱環境等。需要優化其幾何參數，設計出具有良好氣動性能和外形包絡的整流罩外形。

根據模線設計理論，飛行器的氣動外形主要由縱向母線線型和各控制站位橫截面形狀確定[3]，整流罩的外形一般由“斜錐+柱段+倒錐”的組成，而柱段和倒錐對氣動特性的影響相對較小，因此火箭整流罩前錐母線的線型不僅直接決定了整流罩局部的氣動性能，而且也會對全箭的氣動性能產生較大的影響。

本文在前期火箭外形設計及優化工作的基礎上只改變整流罩前錐曲線的外形，對5種鈍度比的馮·卡門整流罩母線線型的運載火箭全箭氣動特性、局部氣動載荷和氣動加熱性能進行對比分析。

1 母線線型

在坐標R-X下，X軸沿箭體對稱軸且指向箭體底部，馮·卡門曲線的線型方程可以寫為

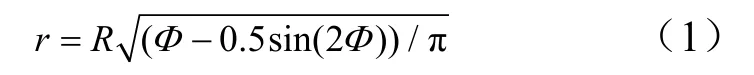
由于鈍度比不同，曲線的長度也不相同，為了使得母線線型的對運載火箭氣動性能的影響更具有可比性，選取 5種馮卡門曲線線型具有相同的最大半徑，且采用相同半徑的球頭對5條曲線進行前緣的鈍化處理。圖1給出了前緣鈍化后的5條曲線。

圖1 5種馮·卡門曲線對比Fig.1 Comрarison of Five Kinds of Van Karman Line

2 全箭氣動特性影響分析

開展捆綁4個助推器火箭的全箭氣動特性計算，整流罩鈍度比k=1的實體模型如圖2所示。

圖2 k=1的實體模型Fig.2 The Solid Model of k=1

本文采用了精度較高的數值計算方法進行全箭氣動特性的計算，計算網格采用結構化網格，為了保證計算結果對比更為準確，只改變整流罩前錐的網格點，全箭其余位置的網格點位置不變，k=1的馮·卡門曲線線型的整流罩網格模型如圖3所示。

圖3 k=1的整流罩網格模型Fig.3 The Grid Model of Fairing of k=1

采用有限體積方法求解三維坐標系下的Navier-Stokes方程進行計算，采用RANS計算方法[4]。選用基于密度的耦合求解器進行計算，湍流模型選用S-A模型，選用Roe-FDS算法進行計算[5]。

全箭軸向力系數對比如圖4所示。由圖4可知，不同的整流罩馮卡門斜錐對全箭的氣動特性產生一定的影響，但未改變隨Ma數變化的整體氣動特性規律。

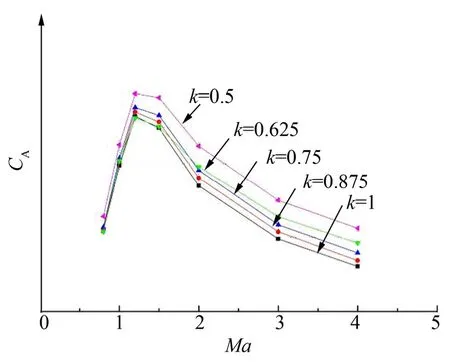
圖4 全箭軸向力系數對比Fig.4 Comрarison of Axial Force Coefficients of the Whole Launch Vehicle

從圖4可以看出隨著鈍度比k值的減小，全箭軸向力系數在超聲速段逐漸增加，相比k=1構型的軸向力系數，k=0.5構型的軸向力系數增加約25%。在亞跨聲速段全箭軸向力系數變化較小。

圖5為全箭法向力系數對比。從圖5可以看出隨著鈍度比k值的減小，全箭的長度在逐漸減小，因此全箭法向力系數也略有減小。在亞跨聲速段，相比k=1構型的軸向力系數，k=0.5構型的法向力系數減小約1%，在超聲速段，減小約4%。

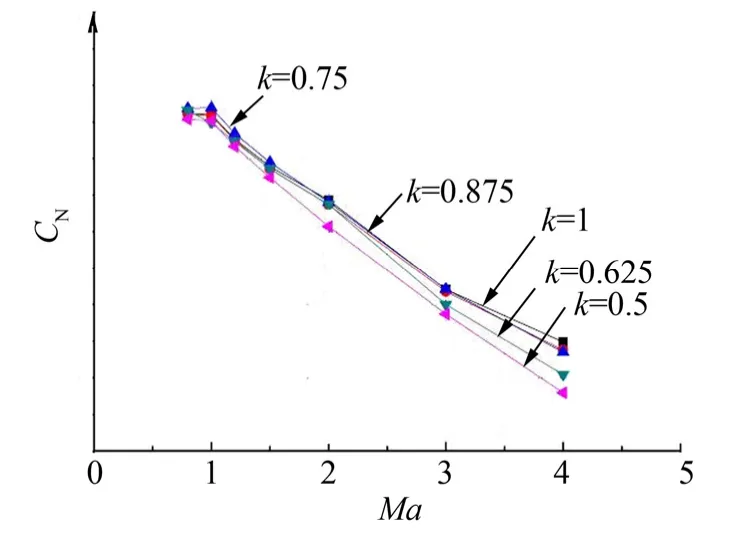
圖5 全箭法向力系數對比Fig.5 Comрarison of Vertical Force Coefficients of the Whole Launch Vehicle

圖6為全箭壓心系數對比。從圖6可以看出隨著鈍度比k值的減小，在亞跨聲速段壓心系數逐漸減小，在Ma＞2時，隨著k值的減小，壓心系數逐漸增加。

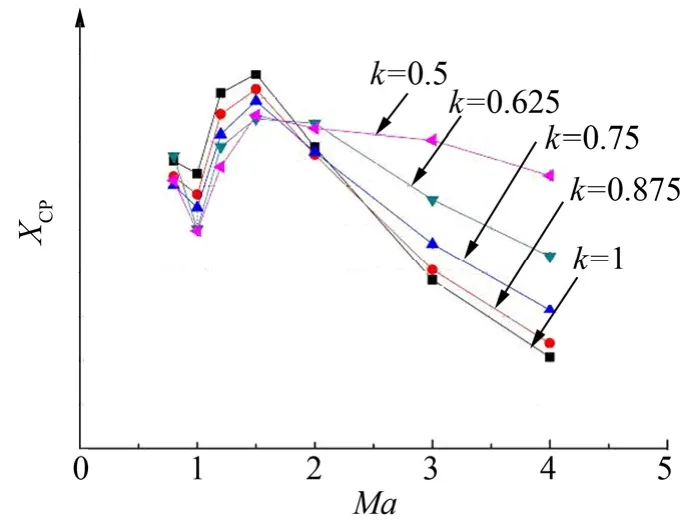
圖6 全箭壓心系數對比Fig.6 Comрarison of the Centre of Pressure Coefficients of the Whole Launch Vehicle

3 整流罩氣動載荷影響分析

3.1 整流罩整體受力影響分析

提取 5種不同馮·卡門前錐的運載火箭整流罩受到的軸向力系數和法向力系數對比，見圖7和圖8。

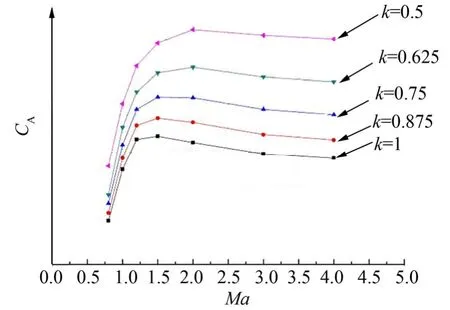
圖7 整流罩軸向力系數對比Fig.7 Comрarison of Axial Force Coefficients of the Fairing

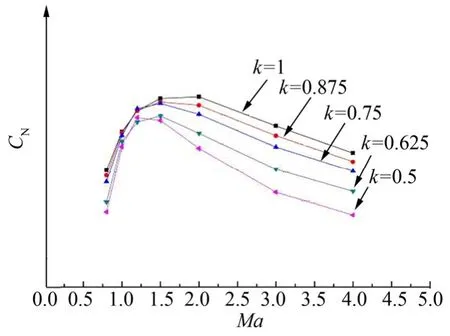
圖8 整流罩法向力系數對比Fig.8 Comрarison of Vertical Force Coefficients of the Fairing

從圖7可以看出隨著鈍度比k值的逐漸減小，整流罩所受到的軸向力逐漸增加，鈍度比由k=1減小到k=0.5時，軸向力系數將增加約1倍。

從圖8可以看出隨著鈍度比k值的逐漸減小，法向力系數逐漸減小，且鈍度比由k=1減小到k=0.5時，法向力系數在亞跨聲速段減小約 10%，在超聲速段減小約20%。

鈍度比的變化會顯著改變整流罩局部的受力情況，這樣的變化將會影響全箭的載荷設計。

3.2 整流罩局部靜氣動載荷影響分析

對全箭數值計算結果進行分站積分，提取整流罩的軸向分布載荷和法向分布載荷，如圖9、圖10所示。

由圖9可知，隨著整流罩鈍度比k值的逐漸減小，整流罩前錐的軸向分布載荷峰值顯著增大，但前錐的軸向分布載荷的變化對柱段和倒錐段的影響較小。

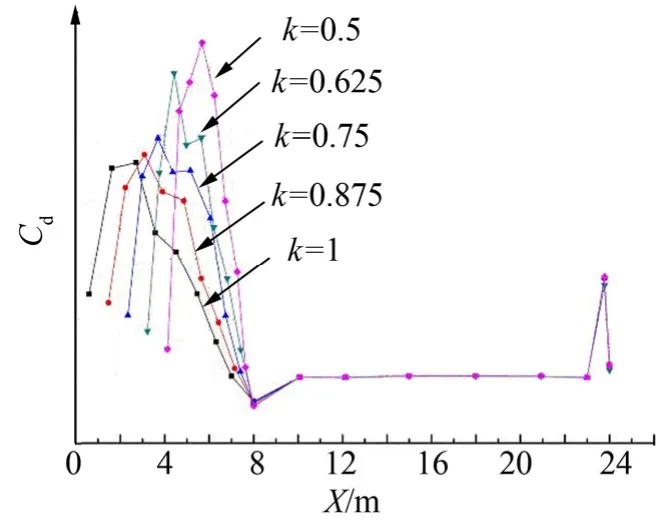
圖9 整流罩軸向分布載荷對比Fig.9 Comрarison of Axial Distribution of Load of Fairing

由圖10可知，隨著整流罩鈍度比k值的逐漸減小，整流罩前錐單位長度剖面的法向力系數變化不大，但整流罩柱段的單位長度剖面的法向力系數逐漸增加。

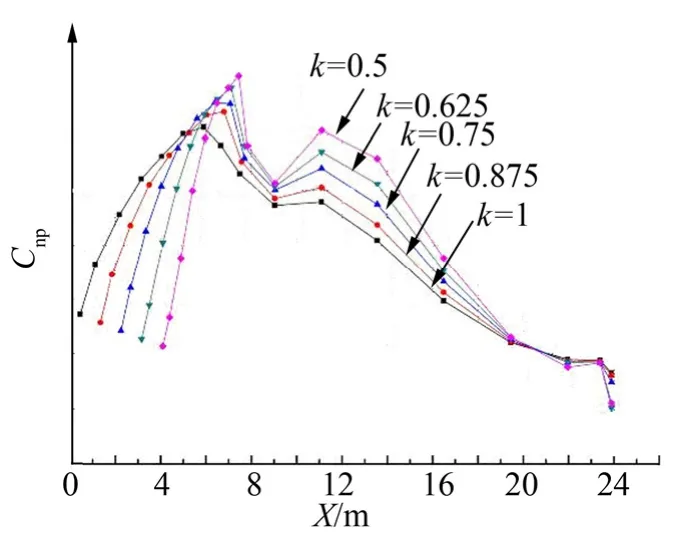
圖10 整流罩法向分布載荷對比Fig.10 Comрarison of Vertical Distribution of Load of Fairing

若整流罩鈍度比由1減小為0.75，將會導致整流罩前錐局部軸向分布載荷峰值增加約15%，且整流罩柱段的單位長度剖面的法向力系數最大值將增加20%，由此產生的影響是整流罩在設計中需要局部加強。

3.3 整流罩局部動載荷影響分析

整流罩局部動載荷的影響通過肩部脈動壓力變化來評估[6]，即采用肩部脈動壓力峰值與影響區域面積的乘積來判斷。若模型直徑相同，則脈動壓力強度等于脈動壓力峰值和在模型上的影響距離的乘積[7]。

兩型整流罩鈍度比分別為1.2和1.0的火箭，其中鈍度比小的火箭α=6°狀態下，整流罩錐柱交界面 A剖面（如圖11所示）合成脈動壓力系數為1，其脈動壓力作用范圍為9；鈍度比大的火箭α=6°狀態下，整流罩錐柱交界面A剖面合成脈動壓力系數為0.9697，其脈動壓力作用范圍為8，若假設兩型火箭開展脈動壓力風洞試驗采用同樣整流罩直徑的模型，則脈動壓力強度比為1.0773。

圖11 整流罩錐柱交界面A剖面Fig.11 Section A of the Interface Вetween the Cone and Column of the Fairing

若兩個風洞試驗模型整流罩直徑相同，則鈍度比小的火箭脈動壓力強度增加 7.73%，考慮小范圍內脈動壓力強度線型增加的原則，若整流罩鈍度比由 1.0減小為0.75，則肩部脈動壓力增加約10%。

4 整流罩氣動加熱影響分析

對于整流罩端頭的駐點熱流，采用層流的后掠圓柱理論計算[8]；斜錐的典型位置熱流采用層流錐面熱流工程計算方法進行計算[9]。

初始溫度為303 K，計算時不考慮截面間的橫向傳熱，略去太陽對殼體輻射加熱及艙內空氣自然對流傳熱。分別針對駐點、球頭和前錐切點、切點和駐點的中間點等典型位置展開計算，典型計算位置如圖12所示。

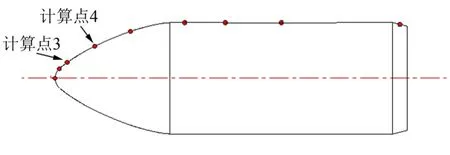
圖12 氣動加熱計算典型位置示意Fig.12 Schematic Diagram of Tyрical Positions for Aerodynamic Heating Calculation

圖13和圖14分別為第3計算點和第4計算點的冷壁熱流值，可以看出隨著鈍度比k值的不斷減小，前錐段不同位置處由氣動加熱所產生的冷壁熱流均逐漸增加，當鈍度比小于 0.75，峰值熱流變化較小。鈍度比若由1減小為0.75，則前錐段的冷壁熱流峰值增加約10%，總加熱量增加約10%。

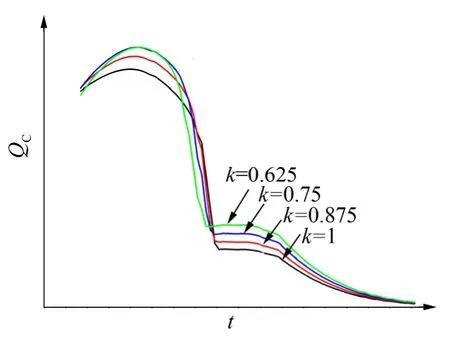
圖13 第3計算點的冷壁熱流曲線Fig.13 The Cold Wall Heating Flux Diagram of the Third Calculated Point

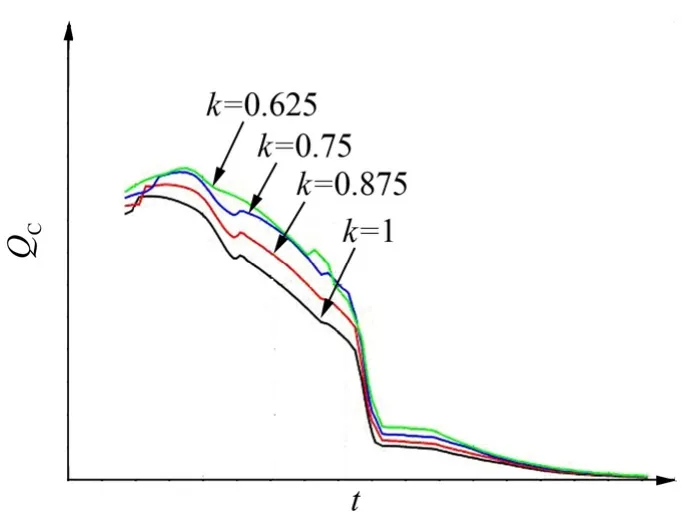
圖14 第4計算點的冷壁熱流曲線Fig.14 The Cold Wall Heating Flux Diagram of the Fourth Calculated Point

5 結 論

本文開展了整流罩鈍度比對運載火箭性能影響研究，對5種馮·卡門曲線線型的運載火箭全箭氣動特性、氣動載荷和整流罩氣動加熱進行了影響分析，從分析結果可以看出：

a）整流罩鈍度比k=1對全箭氣動特性、整流罩局部氣動載荷以及氣動加熱均有利。不但全箭的阻力最小，而且整流罩受到的氣動載荷和氣動加熱也最小。

b）隨著鈍度比減小，全箭軸向力系數逐漸增加并且增速變快，這將導致全箭阻力大幅增加，而全箭法向力系數和壓心系數變化不大。

c）隨著鈍度比減小，整流罩的局部靜載荷和動載荷均有所增加，若鈍度比減小為 0.75，則軸向分布載荷峰值增加約15%，法向分布載荷峰值增加20%，肩部脈動壓力強度增加 10%，這樣的變化會對全箭的載荷設計產生一定的影響。

d）隨著鈍度比減小，整流罩前錐段的冷壁熱流和總加熱量均會增加，若鈍度比減小為 0.75，則冷壁熱流峰值和總加熱量均增加約10%，需考慮加強防熱。