欠驅動水面無人艇魯棒自適應位置跟蹤控制
張成舉, 王聰, 王金強, 李聰慧
(哈爾濱工業大學 航天學院, 黑龍江 哈爾濱 150001)
0 引言
欠驅動水面無人艇(USV)是當前應用較多的海洋工程設備,可進行海洋巡邏、海洋探測等。欠驅動USV位置跟蹤在海洋工程中具有較多的運用,例如敵方艦艇追蹤等。恒定海流的干擾、參數不確定等給欠驅動USV運動控制帶來了困難。
為解決以上問題,Xie等[1]采用級聯控制對欠驅動USV系統軌跡跟蹤進行研究,通過仿真實驗驗證了該控制系統的有效性,但級聯系統較為復雜,工程應用較為困難;王巖等[2]運用滑模控制方法對欠驅動USV實現了路徑跟蹤;王金強等[3]考慮未知海流和水動力學系數不確定的影響,采用自適應方法對未知水動力系數進行補償,通過仿真實驗驗證了該控制系統的穩定性,然而,并未將模型參數不確定考慮在系統中;周佳加等[4]提出一種針對AUV位置跟蹤的改進自適應神經網絡控制器,通過仿真實驗驗證了該控制器的有效性,但是忽略了海流的干擾;王宏建等[5]運用濾波反步法實現了AUV的路徑跟蹤控制器設計,通過仿真實驗驗證了控制器的穩定性,但是并未考慮參數不確定性;Dong等[6]通過運用改進后的反步方法對USV系統進行軌跡跟蹤,效果顯著;Sonnenburg等[7]通過將級聯控制軌跡跟蹤控制器與反步法非線性軌跡跟蹤控制器進行實驗對比,實驗結果表明,基于反步法的非線性控制器比級聯控制器更有效;Wang等[8]提出一種神經網絡自適應濾波反步法,設計了欠驅動AUV三維路徑跟蹤控制控制器,運用徑向基函數(RBF)神經網絡對系統不確定函數進行有效逼近,通過仿真實驗驗證了該控制器的有效性;張偉等[9]將AUV三維路徑跟蹤系統分解為運動學和動力學回路,設計了一種神經網絡動態逆控制器,通過仿真實驗驗證了該控制器的有效性,但是忽略了海流的干擾;徐健等[10]設計了一種基于神經網絡的動態逆控制器,通過仿真實驗驗證了該控制器的穩定性;Yipp[11]針對該問題,提出動態面控制算法,將反步法中虛擬控制變量輸入1階濾波器,濾波后的信號為實際控制輸入,不需對虛擬控制變量逐級求導;Elmokadem等[12]針對欠驅動水下機器人提出采用滑模補償外界干擾,取得了較好的跟蹤效果,但是控制器是基于已知模型的,忽略了模型參數不易準確獲得的難題。
綜合以上國內外研究,雖然一些設計的控制器具有良好的控制性能,但同時考慮海流干擾與系統參數不確定性的相關文獻較少。本文考慮USV系統參數不確定和恒定海流干擾,對位置跟蹤問題開展研究。通過設計神經網絡自適應控制器,對USV系統進行跟蹤控制,并且運用仿真實驗驗證該控制器的有效性。
1 USV控制問題描述
1.1 神經網絡簡述
RBF神經網絡能在一個緊湊集和任意精度下逼近任何非線性函數;本文運用RBF神經網絡逼近未知函數,RBF神經網絡算法為
(1)
f=ω*Th(x)+ε,
(2)
式中:j為神經網絡隱含層第j個節點;x為神經網絡輸入;cj為網絡中心向量;bj為寬度;ω*為神經網絡的理想權值;h(x)為高斯函數;ε為神經網絡的逼近誤差,且ε≤ε0,ε0為正實數。
RBF神經網絡的輸出為
=ωTh(x),
(3)
1.2 USV動力學模型
對于欠驅動USV,設定慣性坐標系為OEXEYE,體坐標系為OBXBYB;對于USV而言,本文只研究水平面內運動控制問題,USV位姿及速度可表示為{x,y,ψ}和{u,v,r},x、y和ψ分別為USV在慣性坐標系下的水平面橫坐標、縱坐標和偏航角,u、v和r分別為USV在體坐標系下的縱向速度、橫向速度和偏轉角速度。USV位置跟蹤如圖1所示,期望運動軌跡為ηh(t),期望位置為xd、yd,運動軌跡誤差為{xe,ye,ψe},xe、ye、ψe分別為慣性坐標系下的位置和偏航角跟蹤誤差。

圖1 USV水平面軌跡跟蹤Fig.1 USV trajectory tracking on horizontal plane
欠驅動USV運動特性,選取簡化后的USV水平面運動數學方程[13]為
(4)
式中:vcx、vcy分別為USV在慣性坐標系下的海流速度。
USV動力學方程為
(5)

由于欠驅動USV系統橫向沒有控制輸入,本文假設橫向速度v有界,所以后文不對橫向速度誤差進行鎮定。
1.3 船體坐標系下位置跟蹤誤差方程
定義USV在慣性坐標系下的期望位置和偏航角為xd、yd和ψd,體坐標系下的期望速度為uc、rc,則可定義USV在慣性坐標系下的位置及偏航角跟蹤誤差為
xe=xd-x,ye=yd-y,ψe=ψd-ψ,
(6)
可得體坐標系下的位置和姿態跟蹤誤差為
(7)
根據(7)式可知,若ex和ey均為0,則xe和ye也為0,反之亦然;本文設計的控制器目的是使ex和ey趨于0附近一個任意小的鄰域中。
對ex和ey分別求導,可得
(8)

2 USV位置跟蹤控制器設計
2.1 鎮定ex和ey
對于USV系統位置跟蹤誤差而言,建立一個李雅普諾夫函數:
(9)
對(9)式求導,可得

(10)
定義一個新的變量:
q=vmsinψe,
(11)
(12)
式中:λ1、λ2為控制器參數,λ1>0,λ2>0;cx、cy為海流觀測器觀測速度。
(12)式代入(10)式,可得
(13)

虛擬控制變量uc和qc通過1階濾波器,可得
(14)
式中:ucf和qcf為經過濾波器濾波后的虛擬控制變量;λu、λq為控制器參數,λu>0,λq>0.
2.2 鎮定eu
定義USV系統的速度誤差變量為
eu=u-ucf,eq=q-qcf,
(15)
(15)式代入(13)式,可得
(16)
定義一個新的李雅普諾夫函數為
(17)
對(17)式求導,可得
(18)
為保證控制系統穩定性,可設定控制輸入τu為
(19)
式中:λ3、η1為控制器參數,λ3>0,η1>0;1為神經網絡權值的估計值,并且神經網絡權值估計誤差
選取自適應律為
(20)
式中:k1、σ1為控制器參數,k1>0,δ1>0.
根據(19)式,可得

(21)
式中:κu=m22vr-Xuu-Xu|u|u|u|.
(21)式代入(18)式,可得
(22)
2.3 鎮定eq
為穩定欠驅動USV系統偏航角,定義一個新的李雅普諾夫函數:
(23)
對(23)式求導,可得
(24)
可設定r的期望值為
(25)
式中:λ4為控制器參數,λ4>0.
(25)式代入(24)式,可得
(26)
虛擬控制變量rc通過1階濾波器,得
(27)
式中:rcf為虛擬控制變量rc經過濾波器的濾波值;λr為控制器參數,λr>0.
2.4 鎮定er
根據(27)式可知,rc是理想虛擬控制量。定義誤差變量
er=r-rcf,
(28)
另外定義一個新的李雅普諾夫函數:
(29)
對(29)式求導,可得
(30)
選擇控制輸入τr為

(31)
式中:λ5、η3為控制器參數,λ5>0,η3>0;3為神經網絡權值的估計值,并且神經網絡權值估計誤差
選取神經網絡自適應律為
(32)
式中:k3、σ3為控制器參數,k3>0,δ3>0.
(31)式代入(5)式,可得
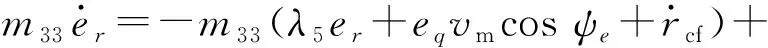
(33)
式中:κr=(m11-m22)uv-m33fr(r)-Nrr-Nr|r|r|r|.
(33)式代入(30)式,可得
(34)
2.5 鎮定和
定義一個新的李雅普諾夫函數
(35)
對(35)式求導,可得
(36)
(21)式和(32)式代入(36)式,可得
(37)
根據文獻[8},可得
(38)
(38)式代入(37)式,可得
(39)
根據文獻[13],可得
(40)

2.6 觀測器設計
為估計恒定海流速度vcx和vcy,采用反步法設計一種自適應海流觀測器[15]。
定義位置x和y的估計值為和,則有
(41)
式中:r11、r21為控制器參數,r11>0,r21>0;εx和εy為位置x和y的估計誤差,則
(42)
對(42)式求導,可得
(43)
選取海流速度估計誤差導數為
(44)
式中:r12、r22為控制器參數,r12>0,r22>0.
定義一個李雅普諾夫函數為
(45)
對(45)式求導,可得
(46)
3 穩定性分析
考慮所設計的位置跟蹤控制器與海流觀測器所組成的閉環系統,通過將系統分解為兩個子系統Σ1和Σ2.
定義子系統Σ1為
‖x1‖=[exeyeueqer]T.
(47)
由于1階濾波器濾波前后存在誤差,為確保系統穩定性,對濾波誤差進行鎮定。定義1階濾波器對虛擬控制變量濾波后與濾波前的差值為
(48)
對方程組(48)式進行求導,可得
(49)
式中:λz為控制器參數,λz>0.
由3個虛擬控制量式,可得
|dzc/dt|≤ζz,z=u,q,r,
(50)
式中:ζz為閉環信號連續特性。
根據文獻[14],可得

(51)
定義一個新的李雅普諾夫函數:
(52)
對(52)式求導,可得
(53)
通過選取合適的控制器參數λ1、λ2、λ3、λ4、λ5、η1、η3、δ1、δ3、λu、λq、λr,可保證子系統Σ1全局一致穩定。

(54)
對(54)式求導,可得
(55)
(44)式代入(55)式,可得
(56)
則子系統Σ2是全局一致穩定的。
建立一個新的李雅普諾夫函數為
V=V6+E2.
(57)
對(57)式求導可得
(58)

(58)式可變換為

(59)

(59)式可轉化為
(60)
綜上所述,閉環系統內所有誤差信號一致有界,所以本文所設計的控制器是穩定的。
4 仿真分析
本文選取文獻[16]欠驅動USV系統模型,驗證設計的控制算法。該USV模型參數為m11=25.8 kg,m22=33.8 kg,m33=2.76 kg·m2,Xu=12 kg/s,Yv=17 kg/s,Nr=0.5 kg·m2/s,Xu|u|=2.5 kg/m,Yv|v|=17 kg/s,Nr|r|=0.1 kg·m2.
選取欠驅動USV初始條件為x(0)=-10 m,y(0)=5 m,u(0)=0.3 m/s,v(0)=0 m/s,ψ(0)=0 rad,r(0)=0 rad/s.
欠驅動USV應用過程中,τu、τr是有限的,在控制器設計中,設定控制輸入為有限值:0<τu<90 N,0<|τr|<20 N·m.

在保證無人艇正常行駛的條件下,經過多次仿真實驗,恒定海流干擾范圍為-0.4 m/s≤vc≤0.4 m/s. 隨機選取恒定海流選取為vcx=-0.2 m/s,vcy=-0.2 m/s. 為驗證該控制器控制性能,選取預期軌跡為xd=0.6t,yd=60sin(0.01t)。
為便于仿真結果分析,仿真時間為1 000 s,可清晰地看出運動軌跡,與文獻[16]中反步法進行對比,仿真結果如圖2~圖7所示。為更好地呈現仿真結果,由于控制器穩定后結果呈現周期性,圖4~圖7展現了前200 s的仿真結果。

圖2 預期軌跡與實際運動軌跡Fig.2 Desired trajectory and practical trajectory

圖3 位置跟蹤誤差Fig.3 Position tracking errors

圖4 速度跟蹤誤差Fig.4 Velocity tracking errors

圖5 函數逼近誤差Fig.5 Function approximation errors

圖6 海流速度觀測誤差Fig.6 Observed errors of current velocity
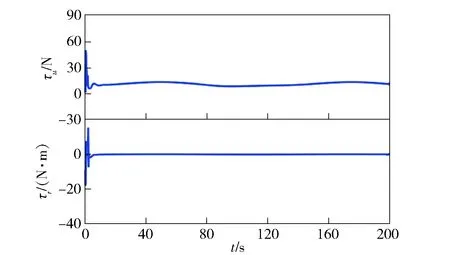
圖7 控制力與控制力矩Fig.7 Control force and control moment
根據圖2可知,提出的控制算法可有效實現預期軌跡跟蹤。根據圖3和圖4可知,欠驅動USV位置跟蹤誤差、速度跟蹤誤差均收斂到0附近的一個鄰域內。根據圖5可知,提出的神經網絡自適應算法可有效逼近未知函數。根據圖6可知,海流觀測器對海流速度的觀測效果較為理想。根據圖7可知,欠驅動USV控制力及控制力矩在設定范圍內,并且較為穩定。
5 結論
本文針對欠驅動USV在恒定海流干擾下的水平面位置跟蹤問題,提出了神經網絡自適應控制策略。得出以下主要結論:
1) 采用神經網絡可對未知函數有效估計和補償。
2) 通過運用李雅普諾夫理論證明了該控制系統的穩定性。
3) 通過仿真結果表明,欠驅動USV位置跟蹤間隙誤差、偏航誤差、速度跟蹤誤差均收斂到0附近的一個鄰域內,從而驗證了該控制算法的有效性。

