壽命服從Weibull分布時高價值彈藥導彈抽樣方法
牛躍聽, 趙暉, 李妍, 穆希輝, 張國志
(1.沈陽理工大學 裝備技術研究院, 遼寧 沈陽 110159; 2.32181部隊, 河北 石家莊 050000; 3.哈爾濱理工大學 數學系, 黑龍江 哈爾濱 150080)
0 引言
近期局部戰爭表明,高價值彈藥導彈已成為現代戰爭依賴的主要彈種。世界各國爭相研制、裝備大量的高價值簡易制導彈藥、導彈。研制生產單位通常會給出高價值彈藥導彈一個大概的質保期,如10 a、5 a. 但是,由于高價值彈藥結構的復雜性、構成材料的多樣性,以及其承受不同環境載荷的差異性[1],導致這個給定的質保期往往和其實際壽命有很大差異,一般給出的質保期都較為保守。
針對臨近質保期的高價值彈藥導彈,世界各國通常的作法是:選取一定數量的高價值彈藥導彈開展壽命試驗[2-4],同時結合自然貯存歷程中的環境載荷,分析光學、機械、電子、化學等部組件失效模式、失效機理[5],分析各部組件壽命匹配的差異性,揚長補短進行延壽修復[6-10],此舉可節約大筆軍費,經濟效益顯著。表1為美軍和我軍部分高價值彈藥導彈延壽情況。

表1 部分戰術導彈、火箭彈、末敏彈延壽情況
表1中的數據來源于美軍導彈研究發展工程中心的導彈壽命周期系統工程面臨的挑戰[11]和我軍有關研究成果。
在高價值彈藥導彈貯存期間內的不同階段,抽取一定數量的樣本進行可靠性試驗時,由于諸多方面的原因,不能像傳統低價值彈藥那樣獲取同年份批次、大樣本來試驗,通常希望通過最小數量的試驗樣本進行統計推斷[12]。但是,樣本容量少,推斷的精度就要減小;另外,高價值彈藥導彈貯存年限不一,如何對其抽樣也對統計推斷的精度產生影響。高價值彈藥導彈樣本數量的確定問題,至今領域內沒有明確的科學依據,各單位只是根據工程實踐經驗,選取6~12個樣本進行評估,缺乏必要的理論依據,有很大的主觀隨意性,對于“抽取多少枚樣本進行壽命評估、抽取貯存了多長時間的樣本、抽取的樣本量和壽命評估精度之間的關系”這一現實問題,很難給出令人信服的答案。
1 考慮貯存時間因素的高價值彈藥導彈抽樣模型
在統計學中,從母體中抽取一個子樣, 確定最少樣本個數,也就相當于確定最小子樣容量。文獻[13]研究了機械行業產品在疲勞壽命試驗過程中最少樣本容量的確定方法。高價值彈藥導彈樣本抽樣有其自身特點:可供研究的樣本數量少、樣本的貯存限對壽命評估有一定的影響[14]、貯存期內有大量的質量監測數據。統計分析這些檢測數據,假設其服從正態分布、指數分布、極值分布、Weibull分布等,運用統計學方法可以得到其最為合適的自然貯存壽命分布函數[15-16]。
貯存的高價值彈藥導彈定期進行質量狀態檢測,抽樣模型符合定時截尾特征。高價值彈藥導彈抽樣時間示意圖如圖1所示。圖1中,X′為貯存期內高價值彈藥導彈壽命變量,X為貯存t1時間后的高價值彈藥導彈壽命變量,Xt2為貯存t2時間后的高價值彈藥導彈壽命變量。

圖1 高價值彈藥導彈抽樣時間圖示Fig.1 Sample time for high-value ammunitions
取分別來自總體Xt1(貯存t1時間后)及Xt2(貯存t2時間后)的兩組樣本,采用定時截尾樣本:
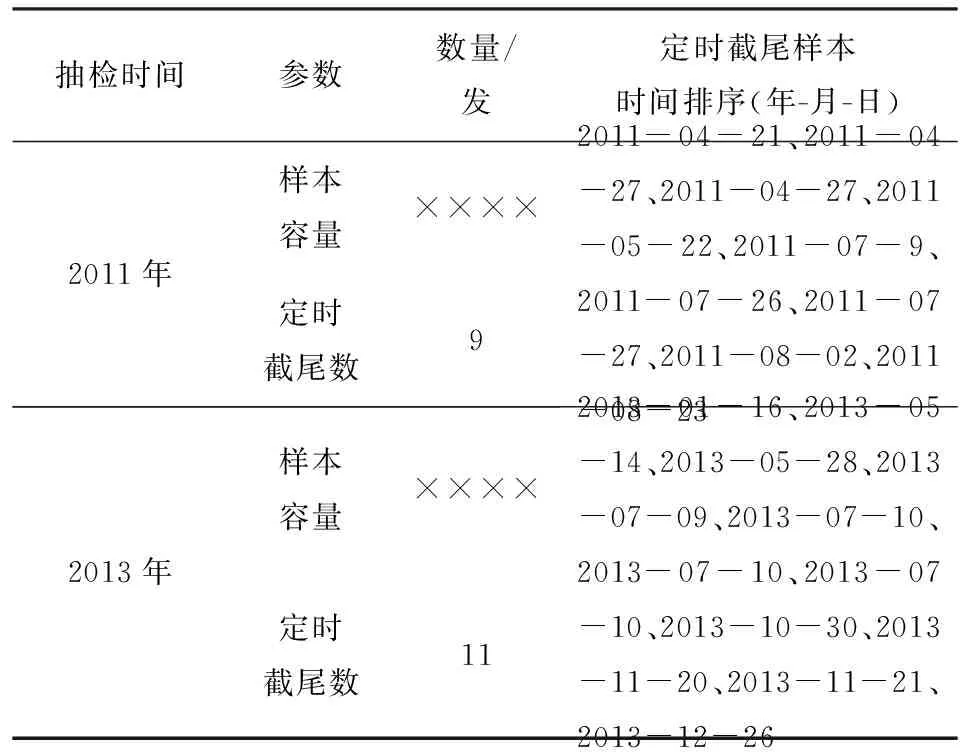
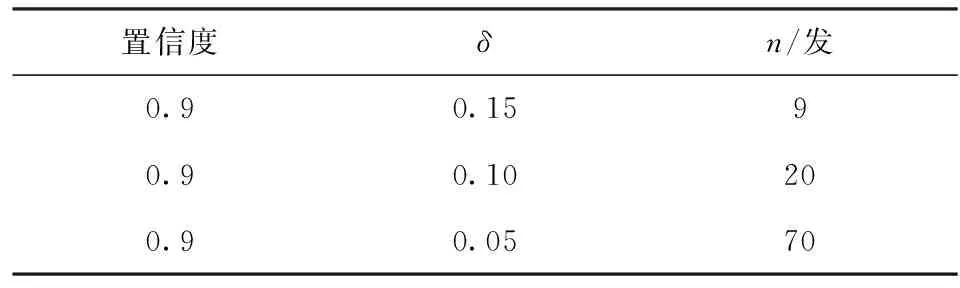
1) 設a1 2) 設q1 統計分析我國某型高價值彈藥導彈長期檢測數據,抽測數量為××××枚,通過壽命分布函數擬合,得出:其自然貯存壽命服從Weibull分布,且形狀參數m=2.3. (1) 變換形式后,得 (2) (3) (4) (5) 由(5)式可得 (6) 數理統計學中有重期望公式: E(Z)=EE(Z|K). (7) 因此,在給定ht0條件下,(4)式可變換為 (8) 在高價值彈藥導彈可靠性評估中,由于Xt0服從Weibull分布,所以高價值彈藥導彈樣本壽命的數學期望為 (9) 將μ置信度為1-α的置信下限估計記為L,可得 (10) 高價值彈藥導彈可靠性評估采用如(11)式精度度量方式: (11) 式中:n為高價值彈藥導彈樣本的容量。 聯立(8)式、(9)式、(10)式、(11)式,可得 (12) r2即為滿足一定評估精度要求條件下,所需要的最小失效樣本數量。由于高價值彈藥導彈可供研究的樣本數量少,因此在工程實踐中為了使其樣本量達到最小(滿足一定評估精度前提下),可取最小樣本容量與r2相等,即:通過壽命試驗,使得選取最小樣本容量的高價值彈藥導彈全部失效,進而通過統計分析的方法評估其壽命。 設定某個精度δ>0,精度要求滿足δn≤δ條件的最小樣本容量n可由(13)式求出: (13) 運用(13)式可以計算得出滿足一定可靠性評估精度要求下,不同貯存時間高價值彈藥導彈的最小樣本容量。 由數理統計學F分布函數的定義可知: (14) (15) 那么,由數理統計學可知: ht0置信度為1-α的置信區間為 (16) 若ht0服從均勻分布,即ht0~U(a,b),0 (17) (18) 抽測了某型高價值彈藥導彈長期檢測數據,抽測數量范圍××××枚,通過壽命分布函數擬合,獲得某型高價值彈藥導彈壽命符合Weibull分布,且形狀參數m=2.3. 其中分別在2011年和2013年抽測的2005年生產某型高價值彈藥導彈統計失效情況如見表2所示,并對數據進行了分析(見表3和表4)。 表2 2005年生產的某型高價值彈藥檢測情況 表3 2011年檢測數據分析 表4 2013年檢測數據分析 取置信度1-α=0.9,查表得: 由(16)式可得ht0(0 表5 最小樣本容量與可靠性評估精度計算結果 由表5分析可知: 1) 針對2005年生產的某型高價值彈藥導彈,在2013年抽樣并進行可靠性試驗時,在置信度0.9、可靠性評估精度指標0.15條件下,最小樣本容量取9. 2) 在同一置信度下,可靠性評估精度指標要求越高(δ數值越小),需要的某型高價值彈藥導彈最小樣本數量越多。 1) 高價值彈藥導彈壽命評估中,可供試驗研究的樣本少,對評估精度影響較大,需要利用統計推斷的理論方法,合理地確定最小樣本容量,為科學評估其貯存壽命提供理論支撐。 2) 高價值彈藥壽命服從Weibull分布時,本文定義了其精度度量方式,研究了樣本容量、貯存時間、可靠性評估精度之間的內在關系,給出了揭示三者關系的數學公式,解決了單發價值高、可供試驗研究的樣本少、貯存年限不一的高價值彈藥導彈可靠性試驗最小樣本容量問題。 3) 任何理論都有使用范圍,本研究中的模型要求p0(p0是[0,t0]區間高價值彈藥導彈的失效率)比較小。工程實際中,貯存10 a的某型高價值彈藥導彈失效率低于5‰,符合這一要求。如果p0大了,模型的誤差就會變大,本文中結論就不再成立。
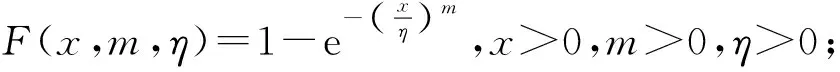

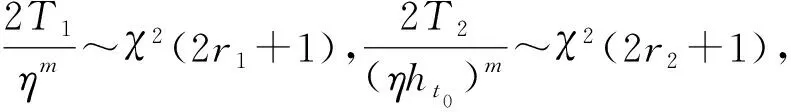

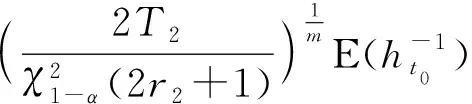


2 ht0的估計





4 算例


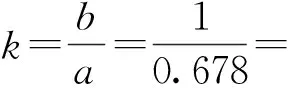
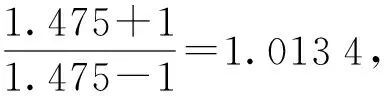



5 結論

