基于模糊局部維數的裝備保障網絡節點重要性評估

張強， 曹軍海， 宋太亮， 閆旭， 張闖

(1.陸軍裝甲兵學院 裝備保障與再制造系， 北京 100072； 2.中國國防科技信息中心， 北京 100142)

0 引言

數字化、信息化裝備大量應用部隊，使得裝備保障工作強度和難度有了梯次性提升，保障組織指揮更加多元化，裝備保障體系戰時布局呈現出網絡化結構。以網絡為中心的裝備保障體系將成為其體系發展的新趨勢[1]。面對敵方不同的攻擊策略，如何挖掘出裝備保障網絡中的關鍵性保障節點，使其得到加強和保護、承擔關鍵性任務，成為裝備保障領域急切需要研究的課題。

裝備保障網絡中不同保障節點之間存在非均勻性和異質性[2]，導致不同保障節點具有不同的重要性，分配保障任務時需要區分對待才能發揮最大保障效能。因此，需要有針對性地選擇裝備保障網絡中重要度較高的保障節點，增加防護力量，從而減少保障網絡中的薄弱環節，增強保障網絡的整體抗毀性[3]。

目前，對于復雜網絡中重要節點的挖掘技術主要有兩類：一類是根據網絡中節點的自身屬性，分析節點的顯著性特征，包括度中心性、介數中心性、子圖中心性[4]、K-核中心性[5-6]、熵權法[7]等；另一類是運用系統動力學思維，從網絡演化發展角度確定節點的重要度大小，包括最短路徑法[8]、節點刪除法[9]、節點收縮法[10-11]、K階傳播數[12]等。由于利用上述單一屬性評估方法確定節點的重要度大小存在一定局限性，學者們開始從其他角度研究并提出可以表征節點多屬性的參數來評價節點重要性。文獻[13]通過定義節點效率和節點重要度矩陣來確定復雜網絡的重要節點；文獻[14]提出了針對無標度網絡的聯合節點重要度貢獻矩陣和結構洞特性的評價方法；文獻[15]基于Dempster-Shafer證據理論，結合節點度數、權重及節點狀態，很好地識別出復雜網絡中影響力較大的節點；文獻[16]運用數據場理論對復雜網絡中的重要節點進行評價；文獻[17]通過凝聚度對節點收縮法進行了改進；文獻[18]運用圖頻譜來判斷社團節點的重要度；文獻[19]通過節點信息熵來對節點重要性進行排序比較；邢彪等[20]從網絡局部屬性指標、傳播屬性指標、連接屬性指標和全局屬性指標出發，結合逼近理想解排序法對裝備保障網絡中節點的重要度大小進行評價。

綜上所述可知，當前評估復雜網絡中節點重要度大小的方法主要存在以下不足：

1)評估節點重要度大小時所選擇的參數大部分只表征節點某一方面的特征，雖然算法效率較高，但只是從某一個側面評估節點重要性，不是很全面。

2)判斷某個節點重要度大小時，僅考慮了其自身屬性，沒有考慮鄰居節點對其重要度所造成的影響。

分析裝備保障網絡的物理結構可以發現，裝備保障網絡的實質是一種復雜網絡，但又與普遍意義上的復雜網絡有所不同：

1)裝備保障網絡中保障節點具有比較明顯的層次性。保障節點的重要性不但與自身所處層次相關聯，還與其鄰居節點所處層次等級息息相關。例如，從運行機制上定性來看，與某基地級保障機構直接相連的保障節點，一般比與基層級保障機構直接相連的保障節點重要。

2)裝備保障網絡中保障節點包括指揮控制節點、維修保障節點、儲存供應節點等，它們種類不同、功能不同，具有較強的異質性；而常規復雜網絡中存在較多同類型節點，例如電網中不同節點之間大都只是地理位置上的區別，異質性表現不是很明顯。通過對大量實際網絡的研究分析發現，復雜網絡本質上的異質拓撲結構決定了網絡中每個節點的地位對等、重要性不同[21]。

3)裝備保障網絡的演化生成規律不同于一般復雜網絡，受到保障任務和裝備保障體制機制的制約。

因此，本文從復雜網絡分形與自相似理論角度著手，借鑒文獻[22-23]中信息維度的概念，提出模糊局部維數的概念，以待評價節點為中心節點一定半徑范圍內的盒子為研究對象，充分考慮范圍內其他節點對待評價節點構成的影響，進而判斷目標保障節點的重要性大小，為進一步優化保障資源配置以及采取恰當有效的防御策略提供參考。

1 裝備保障體系的復雜網絡描述

復雜網絡就是充滿高度復雜性的網絡，表現在拓撲結構復雜、連接關系復雜和演化過程復雜等方面。裝備保障體系是信息化背景下新作戰形態的產物，保障機構種類多、數量大，保障關系復雜，隨著保障任務的推進而演化，這些特點與復雜網絡的特性相吻合，因此裝備保障體系可以構成一類軍事復雜網絡，即裝備保障網絡。裝備保障網絡是在一定區域范圍內(戰區或全軍)，不同級別和不同種類的裝備保障力量單元按照一定的保障要求和配置原則，為達到確定的保障效能而合理部署形成的一個網絡化保障體系，是完成各類保障任務的結構基礎[24-26]。裝備保障體系的復雜網絡描述屬于裝備保障網絡的概念建模，包括節點建模、連邊建模和拓撲結構建模。裝備保障網絡中的節點主要包含維修節點、儲存供應節點以及指揮節點等保障實體；連邊關系包括同級保障節點之間的相互支援關系、上下級保障節點之間的指揮與保障關系、維修節點與儲存供應節點之間的器材供應與需求反饋關系以及越級保障等關系。由于保障體制機制的存在，交互關系頻次較多的就是同級之間的友鄰支援保障關系及上下級之間的指揮關系及器材供應保障關系。這從側面凸顯出一個保障節點的重要性不能單從該節點的特征屬性來判別，而應該聯合該保障節點鄰居節點的一些特征屬性來判別該保障節點的重要性。

裝備保障體系從業務層次上涉及到裝備指揮與管理、裝備維修、裝備儲存與供應(儲供)等，這些環節要由諸多可能分布在不同地域的保障機構完成，包括各級各類維修機構、器材倉庫、基地工廠、各級物資投送機構等保障實體(業務組織關系見圖1)，相互之間通過保障資源的供應關系、支援與被支援關系、信息情報共享關系、指揮關系等相互連接成一個保障網絡。在裝備保障網絡中，各保障機關、保障機構、被保障機構、器材倉庫、維修機構、交通樞紐等作為實體節點，信息流、物流、指揮流以及交通運輸線等作為網絡邊。從大的方面來看，整個裝備保障網絡又可以分為裝備維修子網絡和裝備儲供子網絡，二者構成相依耦合網絡。

圖1 某軍級裝備保障體系網絡的組織結構圖Fig.1 Organization structure of army equipment support network

通過圖1中保障機構的設置分析及預先保障方案，可以得出相應的裝備保障網絡拓撲圖，相應網絡拓撲圖將在第4節保障節點重要性分析中提及。

2 節點重要性參數及評估算法

模糊局部維數是復雜網絡中節點的一種指標參數，可以運用模糊集研究節點中心距離對局部維數的影響。一個節點如果擁有比較高的模糊局部維數，則該節點就具有比較高的重要性。

2.1 復雜網絡的局部維數

復雜網絡理論是研究復雜系統問題的一種重要方法，是由圖論拓展出來的。為了更好地研究復雜網絡的自相似性問題，研究人員將分形理論中的分形維數概念引入復雜網絡中，提出局部維數概念來描述網絡宏觀特點及節點性質[27-29]。局部維數可以通過控制區域半徑的變化綜合體現節點局部信息與網絡全局信息，是用來度量復雜網絡上的節點對其局部網絡結構空間占有有效性的一種參數。

復雜網絡由一系列節點和邊構成，用G(V,E,X)表示，V=(1,2,…,n)為節點的集合，E=(1,2,…,e)為邊的集合，e為保障實體之間連邊的總數目。進行分析研究時，G通常用鄰接矩陣X表示：

X=(xij)n×n，

(1)

式中：xij為節點i和節點j的連接關系，有直接連接關系為1，反之為0.

由于許多現實網絡都服從冪率分布的特性，本文中裝備保障網絡模型也遵從冪率分布，故有：

Bi(r)=μrDi，

(2)

式中：Bi(r)為以節點i為中心節點、半徑r內的節點總數，r為半徑(見圖2示例網絡)；Di為節點i的局部維數；μ為常參數。如果對(2)式兩邊取對數并求導，就得到(3)式：

(3)

圖2 示例網絡Fig.2 Example of network

由于半徑r的不連續性，(3)式可以派生出：

(4)

(5)

式中：ni(r)為到節點i的最短路徑dij等于半徑r的節點數目。

節點i的局部維數Di可以通過(1)式～(5)式結合雙對數擬合曲線的斜率值得到，如圖3所示。節點的重要度與其局部維數呈正相關關系。

圖3 示例網絡中節點的局部維數雙對數擬合曲線Fig.3 Double logarithmic scale fitting curves of nodes in example network

2.2 復雜網絡的模糊局部維數

2.2.1 模糊集

模糊集概念是美國加利福尼亞大學控制論專家Zadeh[30]率先提出的，此概念一出即解決了實際中遇到的中間狀態問題。設論域U(見圖4)，模糊集合A位于U內，若線段元素l位于A內部，則記為1；若元素l位于A外部，則記為0；若l部分處于A內部又部分處于A外部，則是隸屬的中間狀態，通常用隸屬函數表示模糊子集[31]。

圖4 模糊集Fig.4 Fuzzy sets

2.2.2 模糊局部維數

對于與中心節點最短距離小于或等于局部半徑的節點，局部維數是將這些節點視為同等重要，但這些節點的分布往往不都是相同的，因此不能同等看待。顯而易見，距離中心節點越近，對中心節點的貢獻也就越高。基于模糊集和局部維數，本文提出模糊局部維數的概念，通過模糊隸屬度函數來區分局部半徑內的節點。

定義1模糊局部維數。模糊局部維數Df(i)是通過模糊隸屬度函數來區分一定區域內局部維數相同節點重要性的一個參數，描述了節點的屬性特征，其表達式為

(6)

(7)

Nir為節點i和節點j之間最短路徑小于等于ε時的節點數目，Aij(ε)為節點j到節點i距離小于ε時的隸屬度函數，如(8)式所示：

(8)

同局部維數，由于復雜網絡的離散性質，(6)式處理為

(9)

(10)

式中：ni(rt)為最短距離等于區域大小ε的節點模糊數。

通過隸屬度函數可以區分區域半徑范圍內到中心節點距離不同的節點。對于節點最短距離小于半徑范圍內的節點，距離不同時，會有不同的隸屬度，因此也就具有不同的模糊局部維數。如果一個節點的重要性非常不重要，則其模糊局部維數可能為負值。

下面以眾所周知的風箏網絡(見圖5)為例，詳細闡述某一節點模糊局部維數的計算過程。

選取節點7為待研究節點，則rt取值為1、2、3、4. 其模糊數為

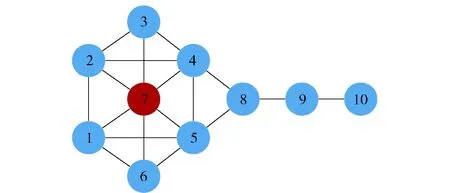
圖5 風箏網絡Fig.5 Kite network

以lgrt為橫坐標、lgN(rt)為縱坐標，進行線性擬合，曲線斜率為0.444 2，則節點7的模糊局部維數即為0.444 2.

2.3 算法步驟

輸入：復雜網絡的鄰接矩陣；

輸出：網絡中每個節點的模糊局部維數。

步驟3將步驟2得到的半徑值rt和模糊數Ni(rt)，畫在x軸為lg (r)、y軸為lgN(r)的雙對數擬合圖中，并計算擬合曲線的斜率，得到該節點i的模糊局部維數。

步驟4重復步驟1～步驟3，得到網絡中所有節點的模糊局部維數。

步驟5根據節點的模糊局部維數對節點進行排序。節點的模糊局部維數越大，其重要性也越高，從而得到節點的重要性大小結果。

由上述算法步驟分析可知，整個算法的時間復雜度與節點之間最短距離計算方法有關。采用Floyd算法計算節點之間的距離，其時間復雜度為O(n3)， 因此該算法的時間復雜度也為O(n3).

3 算例分析

3.1 算法有效性分析

在驗證復雜網絡中節點重要度大小的評估算法有效性時，通常采用美國高級研究計劃署(ARPA)網絡驗證模型[32]。因此，為達到較好的對比驗證效果，本文也采用該網絡模型來驗證所提算法的有效性。該模型拓撲結構如圖6所示，有21個節點、26條邊，平均度值約為2.48，節點平均距離為3.47.

圖6 ARPA網絡拓撲結構Fig.6 Topological structure of ARPA network

根據第2節描述的算法步驟，輸入ARPA網絡的鄰接矩陣，可以得到網絡所有節點的模糊局部維數。節點的重要性排序以及文獻[32-34]中各種方法評價結果對比如表1所示。

由表1中的數據可知，本文算法計算出的最重要節點為節點3，與采用效率矩陣法、節點刪除法和重要度貢獻法得出的結論一致。由于4種評價方法的側重點不同，次重要的一些節點前后排序不盡相同。由此可見，本文算法能夠區分出節點的重要性，表明了算法的有效性。

表1 節點重要度評價結果

3.2 算法準確性分析

根據表1中的數據，采用節點刪除法得到的節點重要性結果中，節點7～節點11的重要度完全相同，但它們會受到其一跳鄰居節點甚至多跳鄰居節點的影響，重要性不會完全相同，而采用本文算法能較好地區分這些特殊節點。與效率矩陣法相比，節點2和節點14的重要性相反。從定性角度來分析，節點1的重要性較節點13和17低，而節點2與節點1直接相連，受到節點1的一部分影響，因此節點14要重要一些，但二者差別并不是很大。因此本文算法能夠區分特殊節點間的重要性差異，取得較準確的評價結果。

4 裝備保障網絡節點重要性分析

以某次戰區演習為例，演習開始前，通過分析作戰保障任務對各保障力量、資源、物資器材等實施調配與部署，構成初始裝備保障體系網絡。其中，設立5個基地級保障節點，下級節點有合成旅修理營、合成旅器材倉庫、修理連、汽車連和基本保障單元等，從而形成不同的社團結構。根據第1節對裝備保障體系網絡的描述以及對某軍級裝備保障體系組織架構的分析并結合文獻[20]，得到戰時裝備保障網絡中各級各類保障節點的對應關系，不同連線表示不同的指揮信息關系，結合保障對應關系，對這些保障機構進行抽象簡化，得到圖7中具有56個保障節點的裝備保障網絡拓撲結構圖。

圖7 某裝備保障網絡拓撲結構圖Fig.7 Topological structure of a equipment support network

由于各保障節點之間的信息、資源聯系是相互的，網絡的邊是雙向的。由圖7得到網絡的鄰接矩陣，進而通過本文算法得到保障節點的重要性結果，如圖8所示。

圖8 保障節點重要性結果曲線Fig.8 Curve of equipment support node importance

由圖8可知：該裝備保障網絡節點重要性排在第一梯次的有節點1、2、3、4、5，與直觀的定性結果一致，屬于基地級保障機構。如果該類保障節點被敵攻陷后，則保障網絡將被劃分為幾個子網絡。節點重要性在第二梯次的有節點9、10、25、27、28、35、38、45、47，這些節點在相應的子網絡中也處于中心位置。剩余重要性在第三梯次的節點較多，在保障網絡中大多處于保障環節的末端。位于同一梯次的保障節點也能通過定量結果進行很好地區分，從而結合預定保障成本，針對性較高地對保障節點進行重點防護，增強保障網絡的整體抗毀性。

5 結論

1)從復雜網絡的分形與相似性出發，本文提出模糊局部維數的概念，利用隸屬度函數區分一定范圍內與中心節點半徑不同的節點，將這些不同鄰居節點對中心節點的影響考慮在內，提出了基于模糊局部維數的節點重要性評價算法。

2)利用本文算法對所建立的裝備保障網絡模型中的保障節點重要性大小進行評價，為進一步分析裝備保障網絡的抗毀性并對關鍵節點進行保護提供了理論支持。