OFDM系統中深度神經網絡指導的IQ不平衡補償算法

劉思琦,王天宇,王少尉

(南京大學 電子科學與工程學院， 江蘇 南京 210023)

同相正交(In-phase and Quadrature-phase，IQ)不平衡存在于系統的收發端兩側，可以分為與頻率無關的和與頻率相關的IQ不平衡，分別由振蕩器和濾波器的非理想特性產生，這種非理想特性導致I、Q兩路上的信號在幅度和相位上產生不同程度的失真[1]。對正交頻分復用(Orthogonal Frequency Division Multiplexing，OFDM)系統來說，與頻率無關的IQ不平衡對于不同頻率子載波信號造成的失真是確定的，它會導致星座點的擴散和相位的旋轉。具體表現為，在時域信號中引入了原始信號的共軛項干擾，即鏡像干擾；在頻域上，該共軛干擾表現為鏡像子載波[2]。而與頻率相關的IQ不平衡對不同頻率的子載波信號產生不確定的失真，導致在同一星座點上的信號產生不同程度的擴散和相位旋轉。它所產生的干擾在頻域上表現為多個其他子載波信號干擾的疊加。這種干擾使得子載波間的正交性被破壞，接收信號無法正常解調，嚴重影響了系統性能。為了解決這一問題，需要對IQ不平衡進行估計和補償。本文主要關注與頻率無關的IQ不平衡的估計與補償。

傳統的與頻率無關的IQ不平衡補償方案可以分為自適應的方案和基于訓練序列(導頻)的方案。文獻[3]提出了一種自適應的估計方法，它將I、Q兩路的不平衡等效到Q路上，然后在接收端的Q路設計一個自適應濾波器，來對IQ不平衡進行估計和補償。文獻[4]提出了一種在頻域上利用自適應濾波器的補償方法，它可以估計每個子載波上的IQ不平衡和對信道的影響。文獻[5]利用訓練序列的頻域結構，對IQ不平衡和信道進行聯合估計。文獻[6]設計了一種特殊的訓練序列結構，同時估計收發兩端的IQ不平衡。文獻[7]聯合考慮了IQ不平衡和相位噪聲的影響，先從頻域獲得的IQ不平衡和相位噪聲的影響參數中分離出IQ不平衡的參數；然后在時域對信號做IQ不平衡補償；最后再回到頻域，并對IQ不平衡補償后的信號做相位噪聲的估計和補償。

深度學習作為機器學習的重要分支，在各個領域(如自然語言處理、計算機視覺等)取得了巨大的成功。它不依賴于有嚴格數學表達的模型，可以僅憑訓練數據生成模型[8-9]。近年來，由于深度學習技術的發展加強了機器學習的計算能力，應用機器學習方法解決無線通信系統問題再次引起了通信專家的注意，許多與深度學習相關的技術也已經被應用到無線通信系統的物理層解決方案中來[10]。文獻[11]提出了一種新的基于自編碼網絡的高峰均比抑制技術，它能更高效地抑制OFDM系統中峰均比過高的問題。文獻[12]提出了一種聯合信道估計和信號探測的深度神經網絡算法，相對于傳統的最小均方誤差(Minimum Mean-Square Error, MMSE)和最小二乘(Least Squares, LS)估計算法，取得了較好的誤碼率(Bit Error Ratio, BER)性能。由于不需要依賴精確的數學模型，文獻[13]證明了深度學習在處理硬件損傷問題時，相對于傳統算法有較大優勢。

本文提出了一種基于深度神經網絡的IQ不平衡估計和補償算法，采用并聯的網絡結構，并利用干擾來自鏡像子載波的先驗知識對網絡進行初始化，該算法可以直接將信號從接收信號的頻域形式恢復為原輸入信號的二進制序列。以誤碼率性能作為評估標準，對比了本文所提算法和傳統的LS補償算法的性能。仿真結果表明，本文算法在幅度和相位失真的補償效果上均優于傳統算法，證明了所提算法的有效性。同時，本文還對比了完全數據驅動和模型驅動的深度神經網絡算法的補償性能，在信噪比(Signal-to-Noise Ratio, SNR)大于15 dB的情況下，模型驅動的算法誤碼率更低，證明了模型驅動的深度神經網絡的優越性。

1 系統模型

本文假設在只有發射端存在與頻率無關的IQ不平衡，在OFDM系統中，與頻率無關的IQ不平衡是由IQ兩路的混頻器在幅度和相位上的偏差引起的。圖1給出了發射端存在與頻率無關的IQ不平衡時的系統模型。

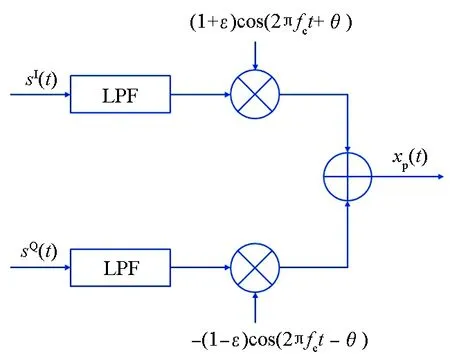
圖1 發射端存在IQ不平衡時的系統模型Fig.1 System model of transmitter with IQ imbalance

圖1中：ε和θ分別為幅度不平衡和相位不平衡參數；sI(t)和sQ(t)分別為I、Q兩路發送端數據的時域形式；xp(t)為發射的帶通信號，其等效低通信號為x(t)。根據圖1，可以得到：

xp(t)=sI(t)(1+ε)cos(2πfct+θ)-

sQ(t)(1-ε)sin(2πfct-θ)

=xI(t)cos(2πfct)-xQ(t)sin(2πfct)

(1)

其中：

xI(t)=sI(t)(1+ε)cosθ+sQ(t)(1-ε)sinθ

(2)

xQ(t)=sI(t)(1+ε)sinθ+sQ(t)(1-ε)cosθ

(3)

則發射端受到IQ不平衡影響的信號x(t)與原信號s(t)有如下關系：

x(t)=as(t)+bs*(t)

(4)

其中：

a?cosθ+jεsinθ

(5)

b?εcosθ+jsinθ

(6)

假設在OFDM系統中，有N個子載波，用FH表示傅里葉逆變換，得到：

s=FHS

(7)

s*=conj(FHS)

(8)

式中，conj(·)表示共軛。

可以得到接收端接收到的受到IQ不平衡影響的信號經快速傅里葉變換(Fast Fourier Transform, FFT)后的頻域表達式為：

Y=HX=H(aS+bS*)=H(aS+bFconj(FHS))

(9)

為方便表達，令Z=Fconj(FHS)。對于發送信號S=[S1,S2,…,SN]T，其共軛項干擾在頻域上對應的鏡像子載波與原信號在頻域上的形式有如下對應關系，即第k個子載波傳輸的時候，接收到的信號是第k個子載波和第(N+2-k)個子載波上信號的疊加，如式(10)所示：

(10)

聯立式(9)～(10)，得到化簡后的接收信號頻域表達形式為：

Yk=aHkSk+bHkZk

(11)

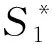
2 并聯深度神經網絡補償算法

本文提出了一種基于深度神經網絡的補償算法，直接將頻域接收信號恢復成原發射信號的二進制序列，即接收機的快速傅里葉逆變換(Inverse Fast Fourier Transform, IFFT)解調器的輸出與訓練好的神經網絡的輸入直接相連，神經網絡的輸出即為待恢復的原二進制序列。其中，深度神經網絡采用并聯的網絡結構，以降低網絡優化的計算復雜度，各并聯子網絡均為全連接的深度神經網絡(Fully Connected Deep Neural Network, FC-DNN)。圖2所示為一個5層的FC-DNN，各層神經元個數為2N、4N、4N、4N、mI。其中：N為子載波數，其輸入層神經元個數為2N，輸入數據為接收端所有子載波上信號頻域表達式的實部與虛部；I為當前網絡估計補償的符號所對應的子載波個數；m為調制階數。每m個神經元對應一個原輸入信號的調制符號，則輸出層共mI個神經元，依次對應輸入I個調制符號的二進制序列。由此得出，每個子網可以估計補償I個并行子載波上符號的IQ不平衡失真，則共需要K=N/I個并聯的子網絡。在一次訓練過程中，子網絡共用一個樣本，其輸入均為接收信號的頻域形式，標記則為各子網絡對應的子載波上原輸入信號的二進制序列，該對應形式可以是隨機的，也可以是按照規則設定的。

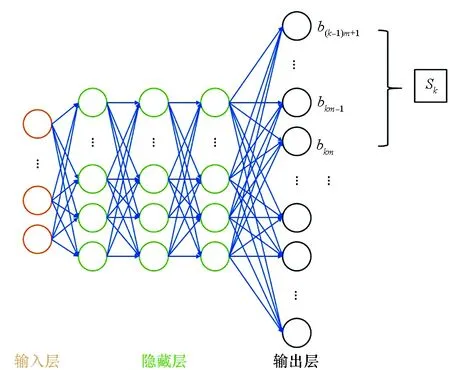
圖2 并聯深度神經網絡的子網絡結構Fig.2 Structure of subnet of parallel DNN

本文提出的補償算法分別訓練了完全數據驅動和模型驅動的深度神經網絡結構。完全數據驅動的深度神經網絡可以只利用數據訓練生成模型[14]，它使網絡不依賴于有嚴格數學表達的模型，在處理一些難以建立精確數學模型的問題(如通信中復雜場景下的信道建模問題，或者硬件損傷問題)時，能獲得更好的性能。而模型驅動的深度神經網絡可以利用特定領域中成熟的先驗知識對網絡進行初始化[15]，從而加快網絡優化的收斂速度，進一步提高系統性能[16-17]。

上述兩種算法的區別在于，是否引入了有效的先驗知識對網絡進行初始化，在本文算法中，網絡的初始化主要體現在各子網絡的輸出層神經元對應補償的符號所在的子載波Sk是否按照先驗知識分布。對完全數據驅動的深度神經網絡來說，各子網絡對應的Sk是隨機的，并聯的網絡結構只是降低了網絡優化的計算復雜度。

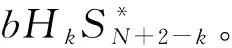
3 仿真與分析

本文考慮在OFDM系統中，采用8 PSK調制。子載波數N=32，每個小批量樣本數據集的樣本數SN=128。則每SN·N個符號作為原信號的一幀。信道采用一般的多徑信道，并加入高斯白噪聲。多徑信道徑數為4，延遲分別為0、3、4、7，單位為采樣點；各徑對應的能量分別為-3.979 4dB、-3.979 4dB、-6.989 7dB、-10 dB。在訓練開始前，將生成的數據集分為三部分，其中3/5為訓練集，1/5為驗證集，1/5為測試集。

對應的并聯深度神經網絡由4個子網構成，每個子網采用相同的結構，各自對應8個子載波上信號的估計補償。網絡采用動量隨機梯度下降優化算法和均方根誤差損失函數，其具體訓練參數如表1所示。其中，輸出層對應估計補償的子載波對于所提兩種算法略有不同。對于完全數據驅動的深度神經網絡模型，輸出層神經元對應的Sk按順序計，它的訓練標記為對應子載波上發送符號的頻域形式[S8(n-1)+1,…,S8n]所對應的二進制序列。

表1 神經網絡訓練參數

模型驅動神經網絡的輸出層考慮將自身鏡像的S1、SN/2+1放在一個子網中，各子網絡對應規則如表2所示。

表2 模型驅動網絡各子網輸出神經元設置

仿真結果如圖3所示，圖中給出了LS算法和本文算法的誤碼率性能對比，其中IQ不平衡參數θ=15°，ε=0.1。從圖中可以看出，在不使用任何補償算法的情況下，誤碼率不隨信噪比的增加而變化，此時接收信號無法被正常解調。對比提出的補償算法和LS算法，所提算法在所有信噪比的情況下，均得到了更好的誤碼率性能。隨著信噪比的增加，誤碼率下降的優勢更加明顯，在SNR為20 dB的情況下，本文算法的誤碼率較傳統算法降低了一個數量級。對比完全數據驅動與模型驅動神經網絡的誤碼率性能，可以看出，在SNR低于15 dB的情況下，兩種算法的性能相似；在SNR高于15 dB的情況下，模型驅動的算法誤碼率性能更好，并且隨著SNR的繼續增加，優勢逐漸增加。

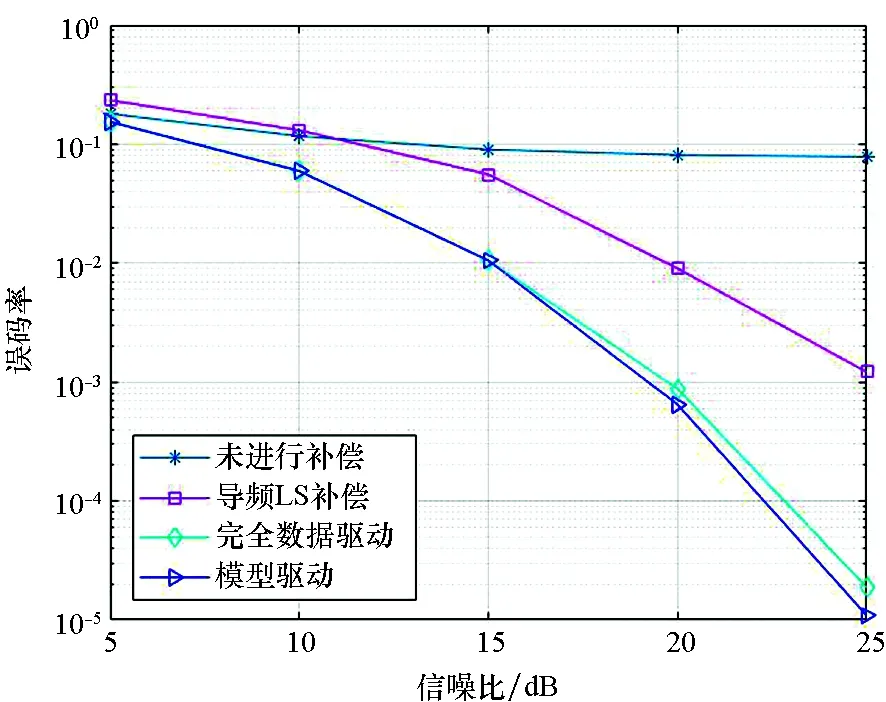
圖3 不同算法的誤碼率性能(θ=15°，ε=0.1)Fig.3 BER performance of different IQ compensation algorithms(θ=15°，ε=0.1)

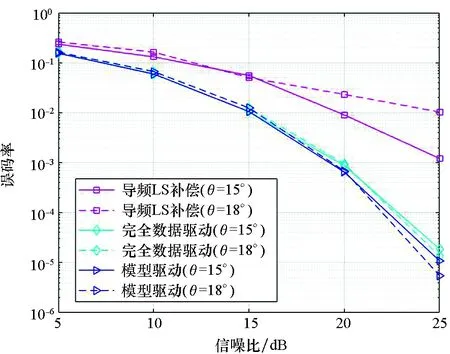
圖4 相位不平衡參數增大對誤碼率的影響(ε=0.1)Fig.4 BER performance comparison with larger phase imbalance parameter(ε=0.1)

圖4給出了在相位不平衡參數增大后，各補償算法得到的BER性能對比圖，其中相位不平衡參數變為θ=18°，在圖中均以虛線表示；對照組相位不平衡參數為θ=15°，在圖中均以實線表示。同時幅度不平衡參數保持為ε=0.1。從圖4中可以看出，相位不平衡參數增加3°后，基于導頻的LS補償算法的誤碼率性能明顯惡化，在SNR為25 dB時，其誤碼率變化從10-3降至10-2，減小了一個數量級。而所提出的兩種算法，其誤碼率性能基本保持不變。這說明了所提算法對于相位不平衡的補償效果要優于傳統算法。

此外，還對比了增大幅度不平衡參數后各補償算法的BER性能，如圖5所示。圖中給出了幅度不平衡參數分別為ε=0.1(實線)和ε=0.12(虛線)時的誤碼率性能對比，此時相位不平衡參數均為θ=15°。從圖中可以看出，幅度不平衡參數增大對各算法的誤碼率性能影響較小，其誤碼率性能變化可以忽略。對比圖4和圖5可以得出，OFDM系統對相位不平衡參數的變化更加敏感。

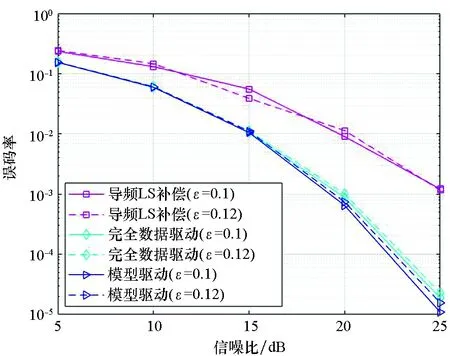
圖5 幅度不平衡參數增大對誤碼率的影響 (θ=15°)Fig.5 BER performance comparison with larger amplitude imbalance parameter (θ=15°)

4 結論

本文考慮了OFDM系統中發射機存在與頻率無關的IQ不平衡問題，提出了一種并聯深度神經網絡架構下的IQ不平衡補償算法。該算法利用深度神經網絡不需要精確數學模型的特點直接恢復原信號的二進制序列，同時，結合IQ不平衡干擾會造成鏡像子載波疊加的先驗知識對網絡進行初始化。仿真結果表明，該算法能有效地對IQ不平衡進行補償，并且其誤碼率性能優于傳統基于導頻的LS補償算法。另外，通過對比模型驅動的深度神經網絡算法和完全數據驅動算法的誤碼率性能，驗證了模型驅動的深度神經網絡更適用于無線通信中物理層的解決方案。仿真結果還表明，在幅度和相位不平衡參數進一步惡化后，相較于傳統算法，所提算法的補償效果能繼續保證較好的誤碼率性能。