小參數對流擴散方程在最優分層網格的一致收斂有限元計算

孫美玲

小參數對流擴散方程在最優分層網格的一致收斂有限元計算

孫美玲

（南通職業大學 公共教學部，江蘇 南通 226007）

面向小參數的奇異攝動對流擴散方程，構建分層網格自適應地刻畫邊界層對應的離散結點，應用有限元計算以期在特殊網格上得到優化結果．分層網格無需復雜計算，僅根據遞推關系可形成隨機剖分數的優化網格，實現更好地捕捉邊界層．數值算例驗證了方法的魯棒性，獲得了完全獨立于小攝動參數、一致收斂的有限元高精度數值結果．

對流擴散方程；小參數；分層網格；有限元法；一致收斂

奇異攝動問題是當前科學工程計算的熱點，廣泛地出現在彈性力學、流體計算、生物系統和運籌控制等眾多領域．在進行數學物理方程描述時，小參數會作為系數出現在方程的最高階導數項，精確有效地求解奇異攝動問題漸進解或近似解一直是相關研究的目標[1-2]．但如果常規處理簡單地將小參數設為零，將導致原方程降階從而不能得到所有的近似解．奇異攝動來源于問題存在多個尺度，為了得到每個尺度的有效近似解，可以將方程用不同尺度分解以得到新方程．

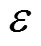
本文考慮一維奇異攝動問題

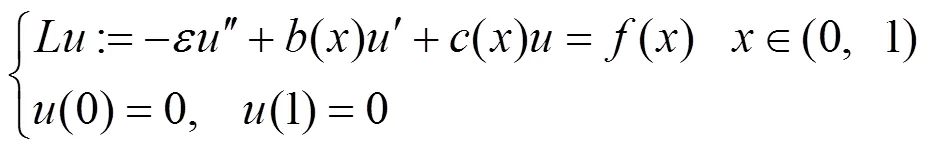
本文研究含小參數問題（1）的精確高效解，應用有限元計算，結合自適應生成的分層網格精確模擬解的邊界層部分和光滑部分，得到與真解相比精度非常高、完全獨立于攝動系數大小的收斂解．

1　有限元的變分處理

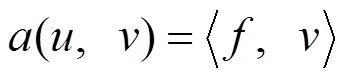
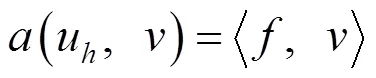
將每一單元形成的單元剛度矩陣累加到所有單元形成總剛度矩陣，求解對應的大規模稀疏線性方程組，即得到有限元數值解．之后還可以對計算結果進行誤差分析與后處理，通過列表和畫圖判斷數值結果的精確程度與收斂性，進一步提升方法的校正和改進性能．

2　分層網格的自適應構建

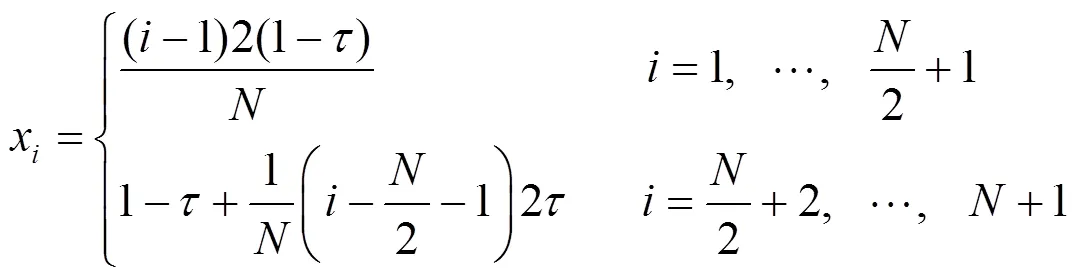
這種分片等距Shishkin網格較之前的分段等距一致網格，能較好地捕捉解的部分奇性．不過Shishkin網格也存在一個缺點，即在某些情形當剖分數為奇數時，可能造成不穩定．

基于一致Uniform網格和Shishkin網格存在的不足，本文給出分層Graded網格（簡記G網格）算法．

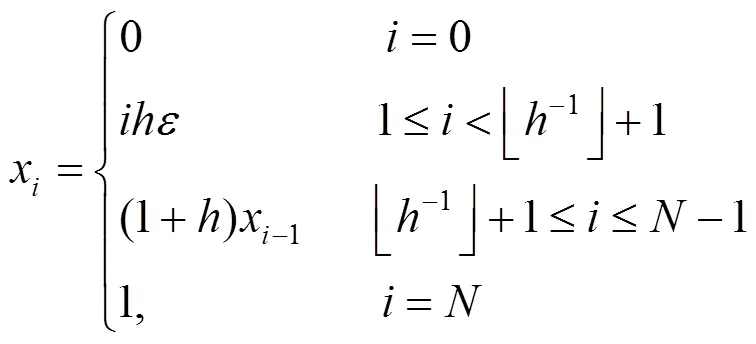
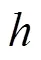
3　程序執行與數值算例

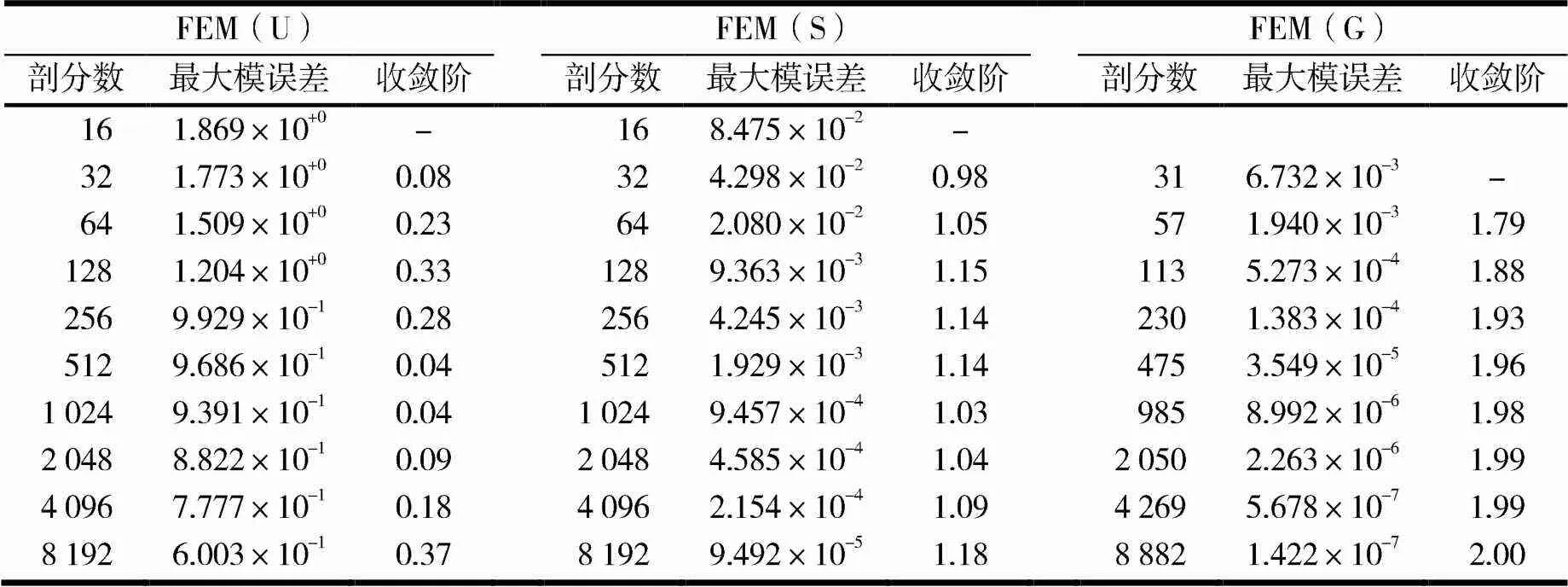
表1　有限元計算在3種網格得到的最大模誤差與收斂階

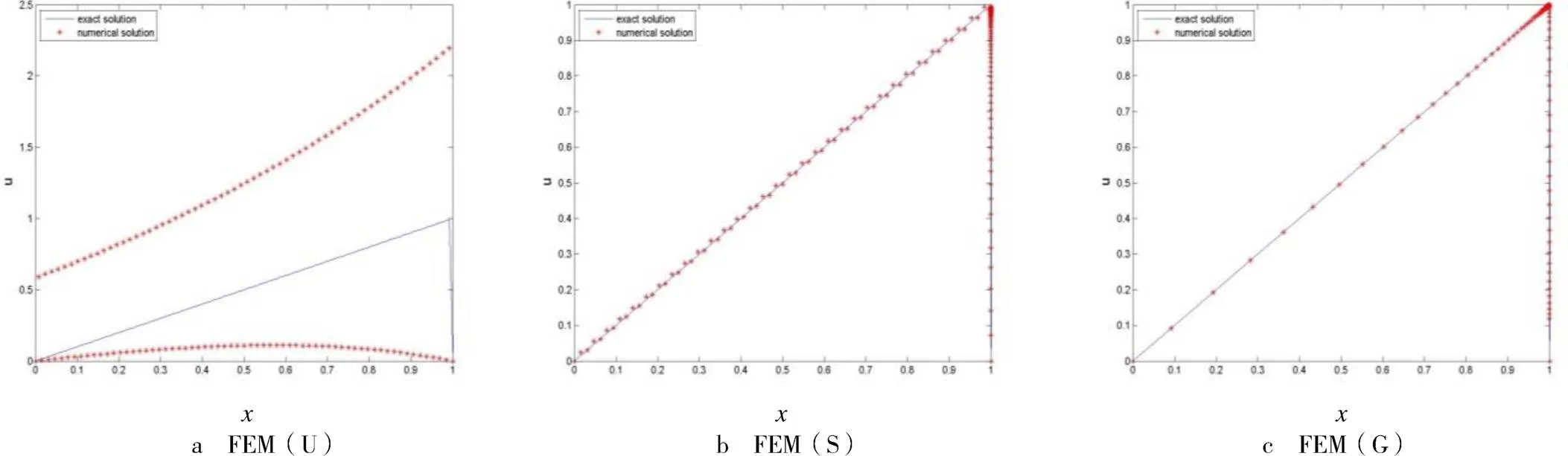
圖1　真解與數值解的對比

本文所提方法能正確高效地模擬小參數引起的奇異攝動邊界層問題，采用分層網格的自適應生成方案并運用有限元計算，獲得了完全不依賴于參數大小且能保證高精度與快收斂的數值模擬結果．

[1] Miller J J，Oriordan E，Shishkin G I．Fitted numerical methods for singular perturbation problems[M]．Singapore：World Scientific，2012

[2] 張偉江，周明儒，林武忠，等．奇異攝動導論[M]．北京：科學出版社，2014

[3] Reddy J N．An introduction to the finite element method[M]．3th ed．New York：McGraw Hill，2006

[4] Roos H G，TeofanovL，Uzelac Z．Graded meshes for higher order FEM[J]．J Comput Math，2015，33（1）：1-16

[5] 王建云，田智鯤．定常非線性薛定諤方程的有限元方法超收斂估計[J]．湘潭大學自然科學學報，2018，40（1）：24-26

[6] Qiu C X，Zhao W J，Song L N．A balanced finite element method of least-squares formulation for singularly perturbed reaction-diffusion problems[J]．Chinese J Engineer Math，2016，33（3）：309-318

[7] Jiang S，Presho M，Huang Y Q．An adapted Petrov-Galerkin multiscale finite element method for singularly perturbed reaction-diffusion problems[J]．Inter J Comput Math，2016，93（7）：1200-1211

[8] Jiang S，Sun M L，Yang Y．Reduced multiscale computation on adapted grid for the convection-diffusion Robin problem[J]．J Appl Anal Comput，2017，7（4）：1488-1502

[9] Chen C J，Chen Y P，Zhao X．A posteriori error estimates of two-grid finite volume element methods for nonlinear elliptic problems[J]．Comput Math Appl，2018，75：1756-1766

[10] 尹云輝，祝鵬，楊宇博．流線擴散有限元方法在分層網格上的收斂性分析[J]．計算數學，2015，37（1）： 83-91

Uniformly convergent finite element computation on optimally graded meshes for the convection-diffusion equation with a small parameter

SUN Meiling

（Department of Public Course，Nantong Vocational University，Nantong 226007，China）

As for a singularly perturbed convection-diffusion equation with a small parameter，a graded mesh is built adaptively to describe the discrete nodes of the boundary layers，and the finite element computation is applied to solve the optimal results on special meshes．The graded mesh is free of complicated operations，it can be realized from a recursive formulation to build the optimal mesh with random partition numbers，which is qualified to capture the boundary layers．The robustness of the method is shown through numerical experiments，the high precision numerical results of finite element are obtained，which are completely independent of small perturbation parameters and uniformly convergent．

convection-diffusion equation；small parameter；graded mesh；finite element method；uniformly convergent

O241.81

A

10.3969/j.issn.1007-9831.2020.06.001

1007-9831（2020）06-0001-04

2020-03-19

國家自然科學基金面上項目（11771224）；南通職業大學自然科學研究項目（1512105）

孫美玲（1981-），女，江蘇南通人，副教授，博士，從事微分方程數值解及其應用研究．E-mail：sunmeiling81@163.com