基于柔性資源約束的前攝性項目調度優化研究

馬 詠，何正文，鄭維博

(1.西安交通大學管理學院，陜西 西安 710049；2.過程控制與效率工程教育部重點實驗室(西安交通大學)，陜西 西安 710049)

1 引言

現有的項目調度問題研究很多是在確定型環境下進行的。然而現實中，大多數項目的執行會受到不同程度不確定因素的干擾[1]，若是在制定進度計劃的過程中不將這一特點進行考慮，那么在項目的執行過程中進度計劃可能會因為受到不確定因素的影響而需不斷的調整，使其失去有效性進而導致項目不能順利實施[2]。而如果資源具備柔性，即資源具備活動實施所需的多種技能，則可以增加制定進度計劃時的靈活性，進而獲得一個魯棒性更大的進度計劃。因此，如何利用柔性資源制定能在不確定環境中穩定執行的進度計劃就顯得十分重要。

項目進度計劃的魯棒性是指在內外部環境因素干擾的情況下，進度計劃能不受影響與保持其穩定執行的能力。對于處在不確定環境中的項目而言，魯棒性較高的進度計劃可以幫助其抵御內外部不確定因素帶來的擾動，確保項目目標的穩定實現。為了得到應對活動工期擾動而不需要重大調整的穩定基準計劃，Herroelen和Leus[3]開發了幾種啟發式算法并對算法進行了評價。Van de vonder等[4]研究了解魯棒性和質量魯棒性之間的權衡關系，并對時間緩沖在項目中的使用方式進行了分析。Al-Fawzan和Haouari[5]考慮了在制定進度計劃時同時兼顧魯棒性和工期的問題。Lambrechts等[6]為生成能抵御由資源可用量變化帶來的擾動的穩定基準計劃，設計了一種禁忌搜索算法。Hazr等[7]研究了魯棒離散時間成本均衡問題，并提出了幾種度量進度計劃魯棒性的方式。壽涌毅和王偉[8]將RCPSP(Resource Constrained Project Scheduling Problem)向不確定方向進行了拓展，構建了問題的魯棒優化模型，并針對模型設計了遺傳算法。何正文等[9]對活動工期具有隨機性、以魯棒性為目標的資源約束項目調度問題進行了研究，在受到項目工期和可更新資源限制的情況下對活動開始時間進行安排，以得到具有最大魯棒性的進度計劃。崔南方等[10]對不確定環境下的Max-npv項目魯棒性調度問題進行了研究。王建軍等[11]為解決并行機環境下工件加工時間可控情況中機器隨機發生故障而使初始調度方案性能下降的問題，以最小化機器故障造成的期望成本為目標，提出了內外兩層嵌套式魯棒調度策略。陶莎等[12]等研究了帶有不確定項目收益交互和資源交互作用的項目組合選擇問題，并構建了魯棒性可調節的魯棒優化模型。Chakrabortty等[13]根據不確定性的特征提出了6種啟發式方法將不確定活動工期轉化為魯棒優化模型中確定性的約束，并對問題進行求解。Bruni等[14]針對活動工期不確定情況下的資源約束項目調度問題構建了可調整的魯棒優化模型，并用一種分解方法求解問題。崔南方和梁洋洋[15]為構建具有較大魯棒性的項目進度計劃，將魯棒性資源分配和時間緩沖插入兩種策略進行結合，設計了一種兩階段集成優化算法。

在經典的RCPSP中，一種資源被認定為只能具備一種能力，即提供一種技能。然而在現實中很多情形下，一種可使用的資源往往能夠表現出多種能力，尤其是涉及到人力資源或工業機器人的情況。工業機器人是綜合機械、電子、控制、計算機、傳感器、人工智能等多種學科的先進技術于一體的復雜智能機器[16]。工業機器人能夠借助編程操作來處理各種零件、材料和工具，以執行各種任務，具有可編程的輸出能力。多技能的人員也可根據所具備的能力用于執行不同的任務。資源柔性的增加產生了多技能資源約束項目調度問題MSRCPSP(Multi-Skill Resource Constrained Project Scheduling Problem)，目前國內外已有學者對其進行了研究。Li和Womer[17]考慮了多技能人力資源約束項目調度問題，研究在滿足工期約束的情況下最小化人力資源使用所帶來的成本。黃敏鎂和羅榮桂[18]針對柔性資源約束下的產品開發項目調度問題進行了分析，提出改進的遺傳算法并運用最大流理論求解出每項任務的柔性資源分配方案。王一帆等[19]提出了一種兩階段優化算法用于解決多技能人力資源約束的項目調度問題。Correia和Saldanha-da-Gama[20]研究了在MSRCPSP中資源固定成本和可變成本帶來的影響。Almeida等[21]提出一種基于并行調度機制的啟發式算法，通過給資源賦予權重和對活動進行分組兩個策略將啟發式算法運用于MSRCPSP的求解。李明和徐哲[22]考慮了項目多技能人力資源調度與指派問題，針對該問題提出了一種優化方法并通過算例實驗驗證了方法的有效性。任逸飛和陸志強[23]以最小化資源投入成本為目標，研究了大型工業品移動裝配過程中的多技能人力資源投入項目調度問題。陳蓉等[24]對存在人員隨機離職環境下的新產品研發項目組合多技能人員調度問題進行了分析和研究。Myszkowski等[25]設計了一種混合微分進化貪婪算法來求解MSRCPSP。Wang Ling和Zheng Xiaolong[26]對同時考慮工期和成本最小化的MSRCPSP進行了研究，并提出了一種知識導向的多目標果蠅優化算法。

資源柔性的考慮使得RCPSP變得更加復雜和符合實際。與此同時，柔性資源可以實現資源間的相互替代，并且允許項目在制定進度計劃時有更多的選擇，以此應對由活動工期變化帶來的不確定性，提高項目的抗干擾能力與執行效率。基于以上項目調度理論和研究現狀，以及考慮不確定因素帶來的擾動終將反映在活動工期的變化上，本文研究具有隨機活動工期的柔性資源約束下的前攝性項目調度優化問題，即在柔性資源及項目計劃工期的約束下，通過對項目各活動的開始時間進行安排以得到具有最大魯棒性的進度計劃。

2 問題界定

在本文中使用AoN(Activity-on-Node)網絡對項目進行表示。若該項目有N個實活動，則在網絡的表述中需添加兩個虛活動：活動0和活動N+1，分別表示項目的開始和結束。在不確定環境中，非虛活動n(n=1,2,…,N)的工期是一個隨機變量，用μ(dn)和σ(dn)來表示其均值與標準差。虛活動0和N+1工期都為0。因為各活動工期是不確定的，所以項目實際工期是一個隨機變量。項目計劃工期D在項目實施的過程中可能會被突破，但在制定項目進度計劃的時候必須將工期約束加以考慮及遵守。

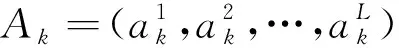
在根據已知活動工期均值μ(dn)所制定的進度計劃中，第n個活動的開始時間為sn。然而在進度計劃的執行過程中，各活動的實際工期可能會偏離均值，從而導致各活動不能按照所制定的進度計劃中的開始時間實施，破壞了進度計劃的穩定性。對于這種情況，可采取給活動留出適當時間緩沖的措施來減輕或吸收由于活動工期變化帶來的擾動，阻止擾動在整個進度計劃上的傳播。因此，本文在活動n(n=1,2,…,N)的計劃完成時間后設置一定時間緩沖Bn，借此提高進度計劃抵抗工期擾動的能力。在已知sn的前提下，Bn可按照下式計算:

Bn=minm∈Un{sm}-[sn+μ(dn)]n=1,2,…,N

其中，Un為活動n的所有緊后活動的集合。在為每個活動設置Bn的時間緩沖后，只要活動的實際工期超過該活動均值工期的幅度不大于Bn，那么活動n工期發生的變化就不會對后續進度計劃的執行產生影響，其緊后活動m也可以按照進度計劃中的開始時間sm實施。

基于上述的討論，可以知道項目進度計劃的魯棒性取決于給各活動制定的開始時間，而活動開始時間又受制于各種資源在項目開始前技能的選擇。因此，本文所研究的問題有兩組決策變量：

n=0,1,…,N+1;t=0,1,…,D

k=1,2,…,K;l=1,2,…,L

為了后文表達需要，進一步定義如下兩個決策向量：

Y=(t:ynt=1,n=0,1,…,N+1)

注意，在這里需要指出的是由于資源的使用是不可分割的，當第k種資源選擇使用第l種技能時，該資源全體都只能用于提供第l種技能。至此，本文研究的問題可以界定為：在滿足柔性資源可用量Rk以及項目計劃工期D約束的條件下，利用已知的資源技能選擇與活動工期參數(包括均值μ(dn)和標準差σ(dn))來確定各活動的開始時間sn，最終實現項目進度計劃魯棒值Robu的最大化目標。

3 模型構建

在對研究問題完成界定及說明的基礎上，構建所研究問題的優化模型，具體表述如下：

MaxRobu

(1)

(2)

m∈Unt=0,1,…,D

(3)

(4)

(5)

l=1,2,…,LT=0,1,…,D-1

(6)

n=0,1,…,N+1;t=0,1,…,D

k=1,2,…,K;l=1,2,…,L

(7)

其中，ST為在T時刻正在進行的活動集合，En與Ln分別表示活動n最早開始時間與最晚開始時間。

在上述的優化模型中，式(1)為目標函數式，要求最大化進度計劃的魯棒值Robu；式(2)指在活動開始時間窗內為其確定一個開始時間；式(3)為活動之間的優先關系約束，用于保證緊后活動m的開始時間sm不能早于其緊前活動n的計劃完成時間；式(4)為計劃工期約束，即虛結束活動N+1的計劃開始時間不能超過項目計劃工期D；式(5)保證對于每種資源，只選擇一種技能進行使用；式(6)為可更新資源技能約束，保證在項目實施過程中的任意一個時刻T，所有正在進行的活動對第l種技能的需求總量不超過資源對該技能的總供給量；式(7)為變量的定義域約束。上述模型中，柔性資源可以通過變換技能的選擇來使技能的供應和項目的需求更好的進行匹配，使得資源能得到更好的利用，并提高制定進度計劃時活動開始時間調整的自由度。在滿足資源和工期約束的情況下，通過對各活動開始時間的不斷調整，各活動會被分配到與其權重系數匹配的時間緩沖，進而得到擁有最大魯棒性的進度計劃。

4 算法設計

RCPSP已被證明為NP-hard問題[27]。本文所研究的問題為具有隨機活動工期的柔性資源約束下的前攝性項目調度問題，是RCPSP向不確定方向的一種擴展。因此，本文所研究的問題也必然為一個NP-hard問題。對于NP-hard問題，因其復雜性較高和求解的難度大，在項目調度問題的研究中一般采用啟發式算法進行求解，包括禁忌搜索算法[5-6,9]和遺傳算法[8,11,18,23-24,28-29]等。本文選擇使用禁忌搜索算法對問題進行求解，具體設計如下。

4.1 算法設計思路

鑒于研究問題的特性，算法總體分為內外兩層嵌套搜索。外層搜索是對資源技能分配方案的滿意解搜索，內層搜索是在給定的資源技能分配方案前提下對于項目進度計劃滿意解的搜索。對于每種資源技能分配方案，運用禁忌搜索算法求得相應的進度計劃滿意解，然后繼續進行資源技能分配方案的禁忌搜索迭代，兩者交互進行，直到達到算法的終止條件，最終目的是為了尋找到使目標函數值最優的資源技能分配方案與項目進度計劃的滿意組合。

內外兩層搜索的具體執行步驟如圖1和圖2所示，其中AL為活動優先次序列表，SL為工期增量列表。

圖2 內層搜索流程圖

4.2 內層搜索算法設計

在給定資源技能分配方案的情況下，所研究的問題轉化成資源約束項目調度問題。設計禁忌搜索啟發式算法對其進行求解。

4.2.1 解的表示及初始可行解構造

解的表示:內層搜索是對活動開始時間安排滿意解的搜索。活動開始時間安排若直接使用活動開始時間進行解的表示，需要多次進行活動優先關系與資源技能關系的判斷，增加了計算的復雜性。因此，在本研究中，用具有滿足活動優先關系的活動次序列表AL與活動工期增量列表SL結合來表示解。

活動次序列表AL：該列表{p0,p1,…,pN+1}由N個實活動和兩個虛活動的序號組成。在制定進度計劃時，活動被安排的先后次序取決于該活動對應序號在列表中的位置。這里需要注意的是pi所對應的活動可能不是活動i，列表中的活動只需滿足優先關系即可。

活動工期增量列表SL：該列表{w0,w1,…,wN+1}由N+2個值組成，每個值表示所對應活動添加的工期增量。與活動次序列表不同的是，在該列表中值wi對應活動i。

基于已知的AL和SL組合，生成進度計劃的具體過程如下：首先，在SL定義的基礎上，令μ(di)′=μ(di)+wi，將μ(di)′作為活動i新的工期；其次，按照AL中所定義的活動優先次序，基于μ(di)′利用串行進度生成機制SSGS(serial schedule generation scheme)可以將一個活動次序列表AL轉換為一個可行的項目進度計劃。

初始可行解構造:步驟1按照活動序號從小到大的順序排列，得到一個滿足活動間優先關系的活動次序列表ALinit。

步驟2為每個活動在指定區間內隨機生成工期增量，并由這些工期增量構成工期增量列表SLinit。

步驟3基于活動次序列表ALinit與工期增量列表SLinit，在滿足資源技能約束的前提下，利用串行進度生成機制SSGS生成一個活動開始時間安排。

步驟4檢查是否滿足項目工期約束，如果滿足約束條件，則將該活動開始時間安排作為初始解；否則，返回步驟2并繼續生成可行活動開始時間安排的操作。

4.2.2 鄰點生成機理

當前可行解ALcurr、SLcurr的鄰點ALneig、SLneig可由如下算子得到：

活動交換算子：在活動優先關系的約束下，隨機選擇ALcurr上的兩個活動并交換活動位置，得到一個新的活動次序列表ALneig。將SLcurr直接記為SLneig。然后基于SLneig和ALneig，利用SSGS生成新的活動開始時間安排。檢查是否滿足項目工期約束，如果滿足約束條件，則將SLneig和ALneig作為一可行鄰點；否則，重新開始生成可行鄰點的操作。

工期增量算子：將ALcurr直接記為ALneig。在SLcurr中，隨機選擇一個活動的工期增量，將該值隨機地變化一個單位，得到一個新的工期增量列表SLneig。然后基于ALneig和SLneig，利用SSGS生成新的活動開始時間安排。檢查是否滿足項目工期約束，如果滿足約束條件，則將SLneig和ALneig作為一可行鄰點；否則，重新開始生成可行鄰點的操作。

4.2.3 禁忌對象

活動交換禁忌TLA：活動交換的禁忌表達式為(Apv,v)。其中，Apv表示pv所對應的活動，v表示活動Apv在交換前列表中的位置。例如，活動次序列表中位置2上的活動3和位置5上的活動4進行交換，則禁忌對象為(3,2)和(4,5)。

工期增量禁忌TLS：工期增量的禁忌表達式為(Ai,wi)。其中，Ai表示工期增量發生變化的活動i，wi表示該活動變化前的增量值。如活動3的工期增量為1，變化后為2，則在工期增量迭代中的禁忌對象為 (3,1)。

4.2.4 算法搜索過程

算法的具體搜索步驟如下：

步驟1構造初始可行解ALinit、SLinit并計算其魯棒值Robuinit；設置算法停止條件：搜索Nummax個可行解;初始化TLA和TLS；初始化計數器Num=0；解的初始化：ALcurr=ALbest=ALinit，SLcurr=SLbest=SLinit，Robucurr=Robubest=Robuinit。

步驟2從兩個算子中隨機地選擇一個，生成一個可行鄰點ALneig、SLneig，計算其對應魯棒值Robuneig。判斷生成鄰點的移動是否在TLA或TLS中，若在TLA或TLS中，轉步驟4；否則，轉步驟3。

步驟3 將鄰點解作為新的當前解：ALcurr=ALneig，SLcurr=SLneig,Robucurr=Robuneig；令Num=Num+1，更新禁忌列表。若Robuneig>Robubest，進一步令ALbest=ALneig，SLbest=SLneig,Robubest=Robuneig,轉步驟5。

步驟4 若Robuneig>Robubest，激活生成該鄰點的禁忌狀態，并對解進行更新：ALcurr=ALbest=ALneig，SLcurr=SLbest=SLneig，Robucurr=Robubest=Robuneig，令Num=Num+1，更新禁忌列表，轉步驟5；否則，轉步驟2。

步驟5判斷Num≥Nummax是否成立，若成立轉步驟6；否則，轉步驟2。

步驟6輸出當前最好解，即ALbest、SLbest和Robubest。

本文中，設計兩個禁忌列表TLA和TLS，分別對應活動次序列表AL和工期增量列表SL。在搜索過程中，禁忌列表按照“先進先出”原則進行管理。禁忌列表的長度通過實驗法確定。

4.3 外層搜索算法設計

4.3.1 解的表示及初始可行解構造

解的表示:資源技能分配方案由所有資源的技能決策向量組成：X=(Xk;k=1,2,…K)。

4.3.2 鄰點生成機理

在本文的研究中，每種資源只能選擇使用一種技能，為了滿足所有的技能需求，可用資源種類數K必須不小于項目所需技能種類數L。根據K與L的大小關系，鄰點生成方式分別如下：

K=L：隨機選擇兩種資源，對這兩種資源所選擇的技能進行變化，得到新的資源技能分配方案，判斷所得資源技能分配方案能否生成可行進度計劃，如能生成可行進度計劃則得到可行鄰點Xneig；否則，重新開始生成可行鄰點的操作。

K>L：隨機選擇一種資源，對其當前選擇的技能進行變化，得到新的資源技能分配方案，判斷所得資源技能分配方案能否生成可行進度計劃，如能生成可行進度計劃則得到可行鄰點Xneig；否則，重新開始生成可行鄰點的操作。

4.3.3 禁忌對象

資源技能變換禁忌表達式為(R,La,Lb)。其中，R表示變換技能的資源，La表示變換后的技能，Lb表示變換前的技能。根據鄰點生成方式分為兩種情形。

K=L：對于兩種所選擇的資源1和資源2，資源1選擇的技能由技能1變為技能2，資源2選擇的技能由技能2變為技能1，則禁忌對象為(1,2,1)和(2,1,2)。

K>L：當前技能分配方案中，資源1選擇技能2，對其選擇的技能進行變換，變換后選擇技能3，則禁忌對象為(1,3,2)。

4.3.4 算法改進措施

改進措施1：當K=L時，對生成新的資源技能分配方案過程中變化技能的兩種資源進行以下判斷：①兩種資源是否有相同的技能數且至少有兩種相同技能。②兩種資源變化前后的兩種技能是否為雙方都具備的技能。如果滿足以上兩個條件，生成新的進度計劃，并判斷是否滿足約束條件；否則，重新選擇兩種資源生成資源技能分配方案并繼續上述操作，直到得到可行計劃為止。

改進措施2：當K>L時，對生成新的資源技能分配方案過程中選擇的資源進行以下判斷：①是否有其它資源與所選資源提供相同的技能。②該資源是否至少具備兩種技能。如果滿足以上兩個條件，生成新的進度計劃，并判斷是否滿足約束條件；否則，重新選擇一種資源繼續上述操作，直到得到可行計劃為止。

4.3.5 算法搜索過程

算法的具體搜索步驟如下：

步驟1將初始可行解Xinit作為參數輸入到內層搜索中，將所得到的滿意解ALbest、SLbest和Robubest作為外層搜索的ALinit、SLinit和Robuinit；設置算法停止條件：搜索Nummax個可行解;初始化禁忌列表；初始化計數器Num=0；資源技能分配方案的初始化：Xcurr=X*=Xinit；外層搜索解的初始化：AL*=ALinit，SL*=SLinit，Robu*=Robuinit。

步驟2如果K=L(K>L),在生成一個可行鄰點Xneig的過程中使用改進措施1(改進措施2)，將Xneig輸入到內層搜索中得到對應的ALneig、SLneig和Robuneig。判斷生成鄰點Xneig的移動是否在禁忌列表中，若是轉步驟4；否則，轉步驟3。

步驟3將鄰點解作為新的當前解：Xcurr=Xneig；令Num=Num+1，更新禁忌列表。若Robuneig>Robu*，進一步令AL*=ALneig，SL*=SLneig,Robu*=Robuneig,轉步驟5。

步驟4若Robuneig>Robu*，激活生成該鄰點的禁忌狀態，并對解進行更新：Xcurr=X*=Xneig，AL*=ALneig，SL*=SLneig，Robu*=Robuneig，令Num=Num+1，更新禁忌列表，轉步驟5；否則，轉步驟2。

步驟5判斷Num≥Nummax是否成立，若成立轉步驟6；否則，轉步驟2。

步驟6輸出當前最好解，即X*、AL*、SL*和Robu*。

5 實際案例

5.1 項目背景與數據提煉

ZSY西南二期軟件開發項目是SST公司為ZSY西南銷售分公司開發的管理信息系統。該軟件開發項目旨在項目實施前，在分析項目活動開始時間延遲所產生損失的基礎上制定出魯棒性高的項目進度計劃，以保證項目在內外部條件發生變化時所受的擾動最小。項目從2008年6月1日開始，計劃于2008年12月30日完工，項目工期為150天。

該項目在實施過程中需要用到三類人力資源：需求人員、開發人員與實施人員。現有的人力資源有需求人員、開發人員、實施人員以及市場人員，可用量分別為4、8、7和4。需求人員主要負責系統需求的調研和分析；開發人員主要負責系統架構設計、組件設計以及程序的編寫和調試等；實施人員主要負責對用戶實施系統進行教育以及咨詢和技術服務等。在SST公司中，各類人員分別具有多種技能。需求人員和實施人員同屬于軟件業務部，能相互承擔對方的工作。開發人員除了能完成自身工作外，還能勝任需求人員和實施人員的工作。市場人員在完成與客戶建立聯系和合同管理等本職工作后，還能協助需求人員或實施人員共同完成任務。

隨著公司業務范圍的拓寬，西安SST有限責任公司經常會有多個項目同時進行的情況發生。每多進行一個項目，就要在當前人力資源分配的基礎上進行調整，這會使其他正在進行項目的人力資源可用量發生變動，人力資源不足會使活動的工期變長，進而導致進度計劃頻繁的調整，活動無法按時開始和完成，甚至項目實際完工時間會超過項目截止工期，給公司帶來損失。多技能的人力資源使得不同種類資源間的相互替代成為可能，一種資源可在另一種資源短缺時派上用場。同時，具有多技能的人力資源能夠在制定進度計劃時提供更大的靈活性，可以提高資源的利用效率和實現進度計劃魯棒性最大化。

該項目共有33個活動組成，需3種技能。項目AoN網絡圖見圖3，其中活動0和活動32分別為虛的開始和結束活動，其余為實活動。各活動的相關參數見表1，其中各活動的標準差是根據歷史數據和實際情況估算得到的。

圖3 ZSY西南二期軟件開發項目網絡圖

表1 算例活動的相關參數

5.2 計算結果

5.2.1 不考慮資源柔性時的技能分配方案

在資源無柔性的情況下，四種人力資源都只具備一種技能，參與項目的有需求人員、開發人員和實施人員，市場人員不會參與到項目中。參與項目的三種人力資源的技能向量分別為(1,0,0)、(0,1,0)和(0,0,1)。利用本文提出的禁忌搜索算法，可求得該項目的滿意進度計劃如下：Y=(0,0,5,6,8,41,9,14,22,38,41,43,48,53,70,53,53,110,114,77,96,101,118,91,96,103,133,70,101,121,143,146,150);Robu=3.76;X=((1,0,0),(0,1,0),(0,0,1))。

由所求得的滿意解可知，項目實際完工時間為149天，進度計劃的魯棒值為3.76，技能分配方案為((1,0,0),(0,1,0),(0,0,1))，即由需求人員提供第一種技能L1，開發人員提供第二種技能L2，實施人員提供第三種技能L3。

5.2.2 考慮資源柔性時的技能分配方案

根據上文對人力資源的描述，一種人力資源可能具備多種技能，具體技能分布情況如表2所示。

表2 資源技能分布情況

由表2可知，只有開發人員具備技能L2，而技能L1和技能L3所有人力資源都具備。為了研究各種人力資源技能擁有情況對進度計劃魯棒性的影響，可在表2的基礎上對資源技能分布進行進一步的細分。因為技能L2為開發人員獨有，只能由開發人員提供技能L2，所以在進一步分析時默認開發人員只具備技能L2。具體細分情況如下：

1)需求人員具備技能L1和L3，實施人員具備技能L3，市場人員具備技能L1。

2)需求人員具備技能L1和L3，實施人員具備技能L3，市場人員具備技能L3。

3)需求人員具備技能L1和L3，實施人員具備技能L3，市場人員具備技能L1和L3。

4)需求人員具備技能L1，實施人員具備技能L1和L3，市場人員具備技能L1。

5)需求人員具備技能L1，實施人員具備技能L1和L3，市場人員具備技能L3。

6)需求人員具備技能L1，實施人員具備技能L1和L3，市場人員具備技能L1和L3。

7)需求人員和實施人員具備技能L1和L3，市場人員不具備上述技能。

8)需求人員和實施人員具備技能L1和L3，市場人員具備技能L1。

9)需求人員和實施人員具備技能L1和L3，市場人員具備技能L3。

10)需求人員、實施人員和市場人員都具備技能L1和L3。

上述10種組合情況對應的資源技能向量及求得的滿意解如表3所示。

表3 各組合技能向量及滿意解

根據上表中各種組合的魯棒值可知，相比資源無柔性情況下的進度計劃而言，資源具有柔性后安排得到的進度計劃魯棒值有了大幅提高，最大值為7.42，進度計劃如下：Y=(0,0,5,7,9,10,10,15,24,37,40,47,52,54,69,54,54,127,131,78,87,98,116,85,90,96,112,69,96,116,137,140,150);Robu=7.42;X=((1,0,0),(0,1,0),(0,0,1),(1,0,0))。

其中，組合1和組合2、組合4和組合5、組合8和組合9這三組組合的對比都表明市場人員具備技能L1較技能L3而言能給進度計劃魯棒性帶來更大的提升；組合3、組合6和組合10中市場人員同時具備技能L1和技能L3，而所得滿意解的資源技能分配方案中市場人員都用于提供技能L1，進一步表明市場人員用于提供技能L1是更好的選擇；組合7是無市場人員參與的情況，同組合8、組合9和組合10對比可知，市場人員的參與能得到一個魯棒性更大的進度計劃。產生以上結果的原因是：市場人員的參與增加了技能的可用量，提高了活動開始時間調整的靈活性，總緩沖時間增加的同時能將緩沖時間更合理地進行分配，進而提高進度計劃魯棒性，而在項目中技能L1的可用量相對技能L3是匱乏的，因此市場人員用于提供技能L1會給進度計劃魯棒性帶來更大的提升。從滿意解的資源技能分配方案可知，最優的資源技能分配情況為：需求人員、開發人員和實施人員分別用于提供技能L1、技能L2和技能L3，市場人員用于提供技能L1。

通過對比以上兩種情況下資源技能分配方案的結果可以知道，SST公司的市場人員具備技能L1使得ZSY西南二期軟件開發項目實際完工時間由149天縮短為143天，進度計劃的魯棒值由3.76提高到7.42，增幅達97.34%。這表明在不確定環境中，資源柔性的增加能縮短項目工期進而幫助項目制定一個魯棒性更高的進度計劃，提高項目抵御不確定因素干擾的能力。

5.3 關鍵參數的敏感性分析

由本文所構建的優化模型可以知道，項目進度計劃的魯棒性受一些關鍵參數的影響，主要有項目工期D、資源可用量Rk和資源柔性。在假定其它因素不變的情況下，單一因素變化對項目進度計劃魯棒性的影響如圖4所示(初始資源技能分配方案為((1,0,0), (0,1,0), (0,0,1), (0,0,1)))。需要指出的是資源可用量的增加為四種資源可用量在原有基礎上同步增加，資源柔性的提高體現在四種資源具備的技能數同步增加。

圖4 進度計劃魯棒性隨關鍵參數變化曲線

各參數的變化情況具體解釋如下:

隨著項目工期的延長，進度計劃的魯棒性近似的呈線性增加。因為項目工期的延長會使項目網絡中所有路徑上的時間緩沖均同步增加，進度計劃擁有的總緩沖變大，進而使得計劃的魯棒性提高。

隨著資源可用量的增加，進度計劃的魯棒性雖在增加，但有減緩的趨勢。因為資源可用量的增加允許活動開始時間能以更大的自由度進行調整，總時間緩沖增加的同時能將緩沖更合理地分配在活動上，進度計劃魯棒性提高。但當資源可用量增加到一定程度時，受項目網絡的約束，活動開始時間調整的靈活性被限制，計劃魯棒性的上升速度減緩。

隨著資源具備的技能數越多，資源的柔性就越大，進度計劃魯棒性也不斷增加。因為資源具備柔性后有更多的技能選擇，可以根據項目的網絡結構和活動對技能的需求量來對應的提供技能，在提高技能利用率的同時縮短了項目工期，給項目留出了更多的緩沖時間在活動中進行分配，進而提高進度計劃魯棒性。

6 結語

本文研究了具有隨機活動工期的柔性資源約束下的前攝性項目調度優化問題。在文中，首先對問題進行界定，將柔性資源定義為具備多種技能但在項目實施前只能選擇一種技能且不可分割使用的可更新資源，采用給活動添加時間緩沖的方式提高進度計劃魯棒性并定義了度量進度計劃魯棒性的方式。研究目標是在滿足柔性資源和項目計劃工期約束的條件下，借助對活動開始時間合理地進行安排進而得到擁有最大魯棒性的進度計劃。隨后，構建了研究問題的優化模型，并根據問題NP-hard屬性和模型特點設計了問題求解的雙層嵌套禁忌搜索啟發式算法，通過內外兩層搜索交互迭代求得滿意解。最后通過一個實際案例對研究問題進行了說明，并分析了項目工期、資源可用量、資源柔性等關鍵參數分別對項目進度計劃魯棒性的影響。研究結果表明：相對于資源無柔性情況下的項目進度計劃而言，資源具備柔性后安排得到的項目進度計劃的魯棒性更高，提高了項目的抗干擾能力，保證項目穩定執行；項目進度計劃魯棒性隨著項目工期的延長、資源可用量的增加或資源柔性的提高而上升。本文的研究將柔性資源約束項目調度問題向魯棒性方向進行了擴展，對在不確定環境中如何制定項目進度計劃可給予決策支持。