基于神經網絡的水電站智能維護方法研究

張 沛

（河南省駐馬店市水利工程質量監督站，河南 駐馬店 463000）

0 引言

水電站智能維護是實現電站運維水平提升的重要途徑，也是當前水電站運行管理的發展方向[1]。因此，基于傳感器的水電站電氣設備監測數據需要整合、分析，并運用到設備的日常運行維護中去。由于傳統水電站運維需要大量人力、物力投入，不僅提高成本，運維工作也不能實現精細化、智能化。為進一步適應智能維護的發展需求，提高水電站電氣類設備的安全性和智能化水平，有必要將一些人工研判的操作轉換為機器自動判別，實現水電站的智能維護。采用神經網絡算法，將設備的監測信息結合歷史運維數據，對電氣設備的管理進行有效指導。

1 基于神經網絡的智能維護模型

1.1 智能維護系統分析

水電站智能維護是繼控制自動化、管理標準化后的又一核心領域，運維費用往往占水電站生產成本的30%左右，其中很多是由運維技術、管理落后造成的不必要支出。采用智能維護方法能顯著提升水電站經濟效益。當前水電站在運行生產中電氣設備的前瞻性維護具有較強邏輯性，可認為智能維護系統是由傳感器感知態勢下，經過神經網絡算法產生的設備自動維護功能系統，包含了電氣設備運行態勢感知數據、神經網絡訓練模型及智能維護決策三部分。設備運行態勢感知層采用總線通信協議，能實現與TCP/IP協議的交互通信。一般而言，水電站電氣設備是水輪發電機、變壓器、輸配電設備等，其中水輪發電機最為核心。由于水輪機在運行過程中，常出現溫度報警、甩油故障等問題，因此需要對其進行前瞻性維護。神經網絡通過模型訓練，獲取數據誤差，并將誤差返回輸出值，并以此調整神經元權重，通過監督學習完成回歸預測，實現水輪發電機的智能維護。

1.2 神經網絡算法模型

水輪發電機調速器通過伺服系統對其葉片開度進行調節，需要有較強的容錯控制，對其建立神經網絡模型，可通過監測系統實現動態監測，伺服系統實現差錯控制。結合水輪發電機結構可知，其伺服系統是非線性的，但故障原因通過經驗總結已形成一套完整的處置流程。因此，神經網絡采用典型的三層結構，見圖1。

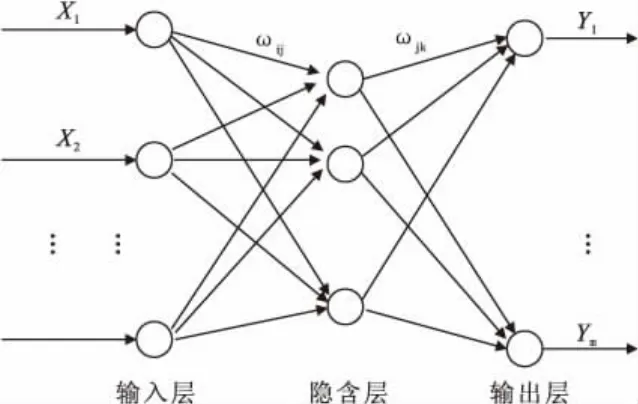
圖1 水輪發電機智能運維神經網絡結構

由于采用前饋調節網絡權值和中間節點閾值，通過誤差傳遞實現各個節點的閾值調節，模擬水輪發電機排查故障的流程，因此建立了水輪發電機物理模型到神經網絡數學模型的映射，為故障處理提供前瞻性[2]。

1.3 神經網絡訓練方法

首先，將網絡初始化。確定輸入層、輸出層以及隱含層節點，并將其賦初值。完成后對節點閾值進行初始化，給定訓練速率和目標函數。

第二步，將水輪發電機感知層數據作為輸入層變量，同時計算出隱含層，見式（1）。

式中:f（·）是神經網絡隱含層目標函數，是典型的指數函數，i為節點數。

第三步，計算對輸出層訓練結果。通過式（1）的結果，并結合閾值a完成第一步的預測結果輸出O，見式（2）。

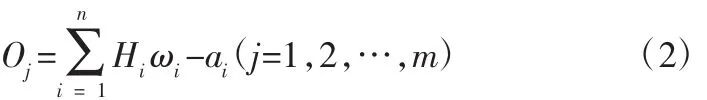
式中:j代表輸出層節點數量。

完成初步結果預算后，應結合水輪發電機故障排查經驗，將其作為期望Y，并完成誤差計算，見式（3）。

根據求得的誤差e，將神經網絡閾值進行步進迭代，完成更新，完成迭代后結束計算。根據實際運行中的水輪電機參數判斷迭代是否完成，修正經驗值。因此，通過水輪電機系統的實時參數可以對水輪機狀態進行監控，并根據故障診斷手冊自動判斷系統故障，提示維護信息。

2 水輪電機故障判定

2.1 故障判定模型

在水電站運行過程中，水輪電機調速器常用PID控制，通過典型的傳統函數可以得到水輪電機模型，因此整個系統的結構[3]見圖 2。

圖2 水輪電機傳遞函數結構圖

通過神經網絡計算出傳遞函數采樣的系統偏差，并輸入PID控制器對水輪電機調速器伺服系統，實現故障判斷，隨動系統、水輪機、負載端的傳遞函數用式（4）、式（5）、式（6）表示。

式中:Ty、Tw、Tg分別代表水輪機接力器時間常數、引水慣性時間常數、水輪電機組時間常數；ey、eh、eqy、eqh、en為系統傳遞函數的系數。

板橋水電站水輪機調速器系統設計水輪電機組時間常數為6 s、引水慣性時間常數為2 s，水輪機接力器時間常數為0.2 s，系統傳遞函數為2，用系數為1作為傳遞函數模型初始值，輸入神經網絡進行計算。按照上述控制模型，傳感器將周期采樣結果與神經網絡輸出結果進行比對，并通過誤差修正網絡。通過以往的運維方案，建立水輪電機兩種輸出值判別模型，見式（7）。

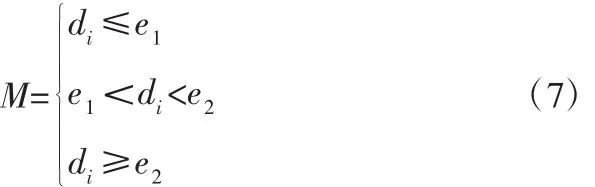
式中:M代表處理模型，di代表神經網絡輸出結果與傳感器監測結果的差值，e1為降階處理的閾值，e2為故障報警的閾值。

通過這一模型可以對水輪電機的調速器系統做出相應的運維響應。當差值小于降階處理閾值時，調速系統可以暫不做處理，僅做可接收誤差記錄；當差值大于降階處理閾值時，調速系統因根據神經網絡輸出結果進行調參，并帶入神經網絡直至迭代到合理范圍；當差值大于故障閾值，系統直接發出維修報警，運維人員經查看做出相應的處理。

2.2 故障測試樣本

通過傳感器監測到水輪電機組的振動基頻、振動高頻、系統振頻、振動—轉速相關性、振動—引水流量相關性作為神經網絡的特征向量輸入網絡進行迭代，并進行歸一化處理。訓練樣本及測試集見表1、表2。

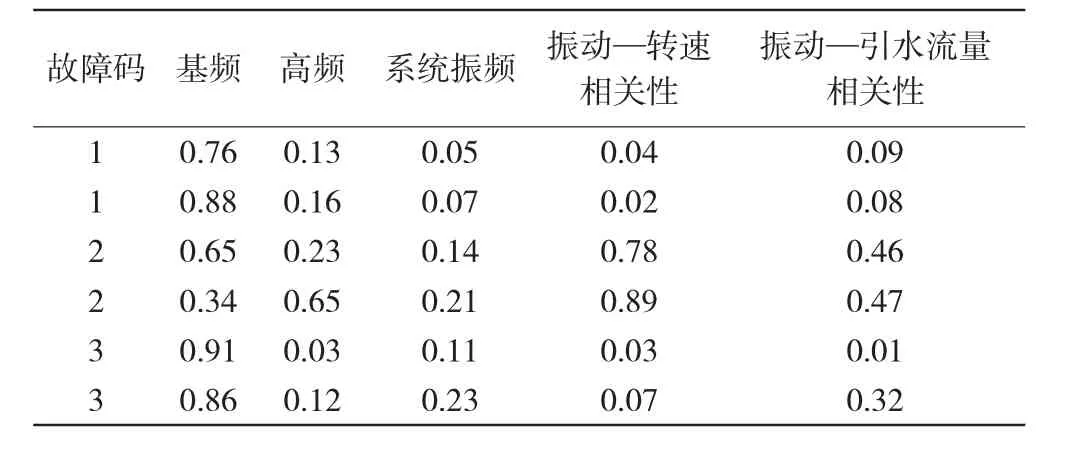
表1 故障樣本訓練集

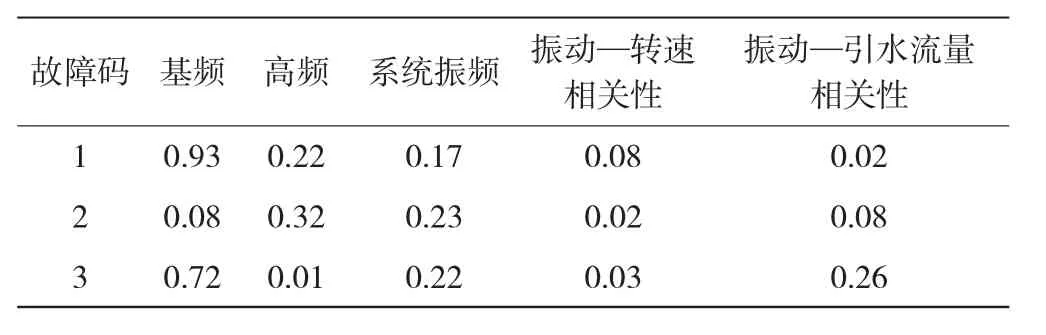
表2 故障測試集

3 結果分析

3.1 故障測試集結果分析

按照板橋水電站設計參數帶入模型，將神經網絡初始化。選定測試節點，通過神經網絡計算某測試周期內的輸出值，根據傳感器歷史測量結果作對比，獲得周期內系統故障參數，并通過其變化判定故障和處理方法。在迭代271次，優化64次后，網絡曲線收斂，完成了迭代。將訓練集結果用測得歷史故障參數進行測試，并按照2.1中方法進行故障判斷。三組測試樣本的實際故障為系統過載運行、水力不平衡及轉子失衡，神經網絡診斷的結果和實際的故障結果一致性達100%，完成了測試集的正確診斷。測試結果見表3。

表3 神經網絡判別結果

通過測試結果看出，當故障時的傳感器歷史測量參數輸入網絡，通過迭代得到的故障判別類型，可以有效預測水輪電機調速系統的未來故障趨勢，為了更進一步說明該方法的有效性，將轉子不平衡故障以故障判別式進行匹配。如系統正常運轉中，轉子不平衡故障在臨界轉速下，隨著轉速增加而導致的振幅增加，而引起的系統振頻瞬時增加。當系統振頻與神經網絡預測振頻差值到達報警閾值時，系統報警；達到停機閾值時則系統停機。測得結果見圖3。

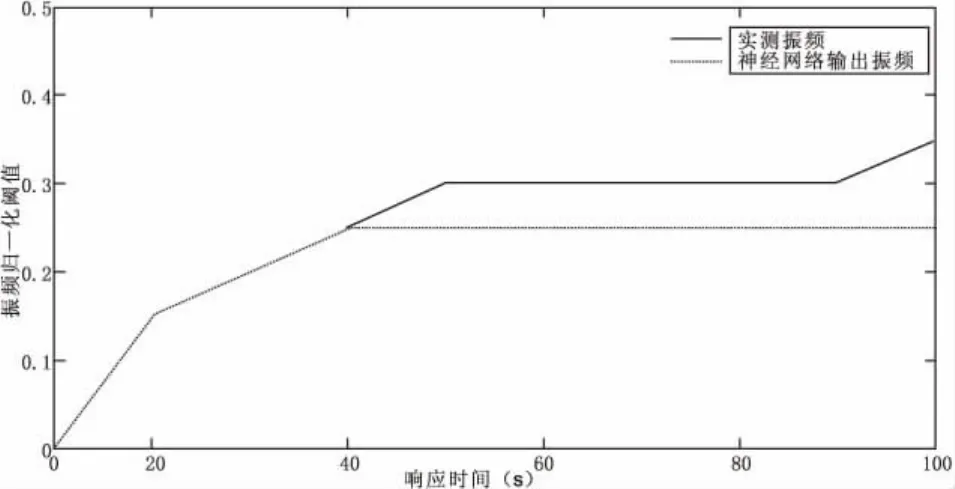
圖3 轉子不平衡導致振頻增加

從圖3可知，當響應時間在20 s后，轉子不平衡引起系統振頻增加，實際測量系統振頻隨時間增加一直增加，且一直達停機閾值才會報警；神經網絡訓練模型能在40 s時對系統做出響應，通過相應的轉速調節降低振頻，使系統不高于停機報警閾值，且一直處于故障報警閾值之上，符合2.1中的故障判別條件2，因此系統報警推送至運維人員，在一定轉速能實現定期維護的功能。

3.2 閾值與神經網絡對比

將原水輪電機閾值故障判別方法與基于神經網絡的故障判別方法進行對比。兩種數據集帶入模型進行迭代，訓練完成后，誤差絕對值控制在0.4%以內，但可以明顯看出，PID閾值判定的故障誤差高于神經網絡故障判別，在迭代超過120次后，神經網絡誤差曲線明顯收斂，并高度接近真實故障測得樣本，因此三種故障的判定結果準確率能達到100%，兩種數據集訓練的平均誤差曲線見圖4。

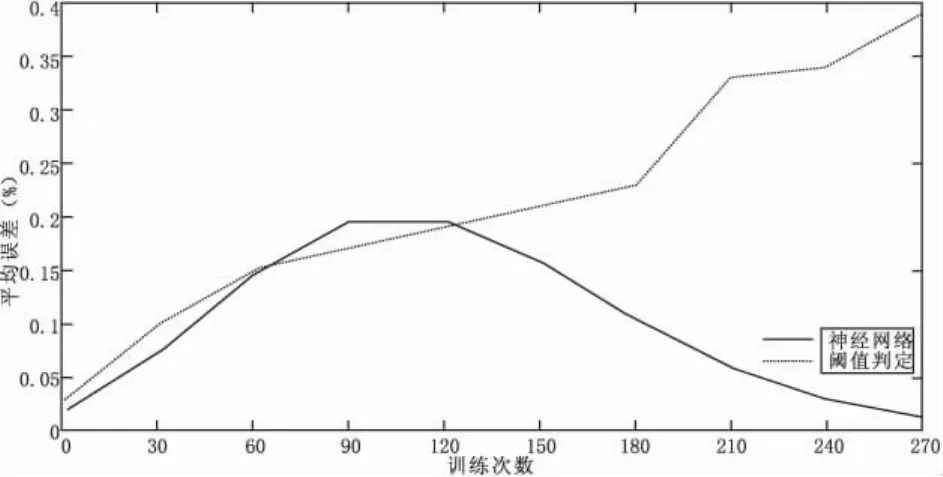
圖4 兩種數據集誤差結果

4 結語

經測試，神經網絡在對水電站電氣設備的故障判定上有較強的非線性逼近能力，水輪電機故障具有較強的非線性特征，可以用神經網絡解決傳統閾值判斷故障的準確率低問題；同時，神經網絡通過迭代后，輸出結果誤差接近泊松分布，可以有效地為水電站智能維護提供預測和判斷。