基于互相關目標函數的反射波波形反演

李青陽 吳國忱* 段沛然 梁展源

（①中國石油大學（華東）地球科學與技術學院，山東青島266580；②海洋國家實驗室海洋礦產資源評價與探測技術功能實驗室，山東青島266071）

0 引言

在聲波全波形反演（FWI）中，密度與速度高度耦合是密度反演最大的挑戰［1］，并且密度變化對地震波的振幅影響更大，而不能改變地震波的走時，因此在FWI研究中往往忽視密度反演。然而密度是重要的地下介質物性參數之一，可靠的速度、密度信息對儲層評價、巖性解釋和油藏描述等具有重要意義［2］。由于密度與速度參數之間存在耦合效應，選擇不同參數化模式有利于降低二者間的串擾。何兵紅等［3］列舉了速度—密度、模量—密度、阻抗—密度、阻抗—速度、模量—速度及模量—阻抗等6種參數化模式，認為阻抗—速度參數化模式去耦合效果最佳，但是不能直接獲取密度模型，無法避免速度和密度之間的耦合性。K?hn等［4］指出，在任何參數化模式下密度反演效果均最差，但速度—密度參數化模式優于模量—密度。由此可見，選取最優參數化模式反演密度的效果是有限的，因此期待以合理反演策略提高反演精度。Jeong等［5］在頻率域組合多種參數化模式反演速度、密度參數精度較高，但其使用的超低頻（0.167Hz）信息實際意義不大。Prieux等［6］首先用大炮檢距地震數據反演速度，再用全炮檢距地震數據反演速度和密度以提高密度反演的穩定性，并指出速度—密度參數化模式優于速度—阻抗。張廣智等［7］首先固定密度反演出速度參數作為初始速度模型，再同時反演速度和密度的效果較好。Luo等［8］提出基于散射角分離的多尺度速度、密度反演方法，并獲得良好的效果。

上述研究均認為速度—密度參數化模式是密度反演的最佳模式，其密度反演存在強烈的高波數偏移特性，即反演只聚焦于模型的高波數成分，因為小入射角反射波在密度反演中權重太大［9］。FWI需滿足地震數據含低頻信息、炮檢距足夠大和相對精確的初始模型［10］等條件。傳統FWI明顯依據低頻數據和潛水波信息恢復模型參數的長波長分量［11-12］，這種方法在密度反演中不適用，因為密度擾動對大炮檢距反射信息不敏感，主要與中、小炮檢距反射信息有關，實際上中等炮檢距數據更常見。當前隨著圖形處理器（GPU）并行計算逐漸成熟及計算設備性能的提升，三維FWI發展迅速，而其龐大的數據和計算量對計算機內存和性能帶來極大挑戰［13］。

綜上所述，常規FWI恢復密度模型的低波數信息難度較大［9］。針對反射波數據主導的低波數速度建模，Xu等［14］提出反射波波形反演（RWI），通過真振幅偏移/反偏移構建反射波能量［15］，利用反射能量恢復模型深部背景速度。Wang等［16］實現了頻率域RWI，指出低頻信息對RWI不可或缺。Mora［17］認為FWI分為偏移過程和層析過程。Alkhalifah等［18］指出，傳統RWI更利于更新模型短波長成分，通過分離反演梯度的長波長背景速度分量和短波長速度分量建立一個聯合目標函數，同時更新背景速度和速度界面，從而有效增強層析效果。由于RWI對初始模型仍然具有一定的依賴性［19］，因此Chi等［10］利用模擬記錄與觀測記錄的互相關建立目標函數，提出互相關目標函數的RWI方法。Luo等［19］提出全旅行時反演，通過Rytov近似（一種常用的波動方程線性近似解，用于計算散射波場，與之并列的方法有Born近似、De Wolf近似、WKBJ近似等）分離振幅和旅行時信息，建立旅行時核函數，進一步提高反演的線性特征。Wang等［20］將RWI推廣至彈性波反演，利用P-P波成像作為縱、橫波偏移結果進行反偏移獲取散射波場；隨后，提出基于彈性波P/S分解的反射波旅行時反演，以此增強縱、橫波速度反演的線性特征［21］。Wang等［22］通過波模式分解分析了彈性波旅行時反演的敏感核函數。Ren等［23］提出敏感核分解的反射波反演方法，獲得了較好的實際效果。付繼有等［24］研究了聲介質的基于波形互相關的反射波反演方法，利用動態圖像校正方法拾取旅行時差。崔超等［25］提出基于雙差的波動方程反射波旅行時反演方法，提高了動態圖像校正方法拾取旅行時的精度。

鑒于RWI能夠反演密度模型的低波數分量，將其與FWI結合能夠更準確地反演密度模型。但與常規速度反演不同，密度RWI提供了近乎全部的低波數信息。因此，本文提出基于互相關目標函數的反射波波形密度反演方法，建立了基于RWI＋FWI的速度—密度雙參數反演流程。首先回顧了傳統聲波變密度方程雙參數反演，并利用輻射模式分析了密度反演的偏移特征；然后提出基于速度和密度經驗公式的RWI方法；再結合傳統FWI方法重建真實的速度、密度模型；最后通過簡單雙層模型和重采樣的Sigsbee 2A模型進行反演測試，以驗證方法的有效性。

1 理論

1.1 傳統密度反演回顧與偏移特征分析

時間域變密度聲波方程為

式中：p（x，t，xs）為t時刻、空間位置x處的壓力場，xs為震源位置；ρ（x）為密度；v（x）為速度；f（t）為震源函數。

聲波FWI通過構建最小二乘約束使由初始模型得到的正演模擬記錄pcal和觀測記錄dobs的波場殘差最小，進而采用最優化方法獲取地下介質的彈性參數m，目標函數為

式中：xg為檢波點位置；g、s分別表示檢波點、炮點。

根據E（m）計算梯度即可迭代更新密度模型

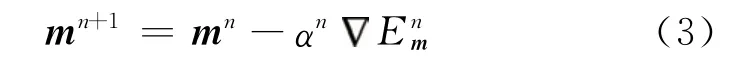
式中：n為當前迭代次數；α為迭代步長；Em為目標函數對密度的梯度。

李青陽等［26］根據伴隨狀態法［27］推導速度、密度梯度精確表達式，并借助等效交錯網格［28-31］實現正、反演數值模擬。速度、密度梯度為

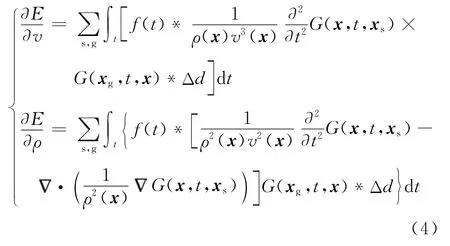
式中：G表示Green函數；“*”為褶積運算符；Δd＝pcal（xg，t，xs）－dobs（xg，t，xs）為波場殘差。

至此，已建立傳統速度—密度FWI理論框架，然而要獲得準確的密度反演結果難度較大。傳統反演方法很難恢復密度模型的低波數分量，這是由于炮檢距敏感性因素和頻率因素所致。

1.1.1 炮檢距敏感性因素

在速度—密度FWI過程中，入射波穿過擾動介質產生散射波，而散射波場作用于模型更新量。因此首先分析速度—密度輻射模式［32］

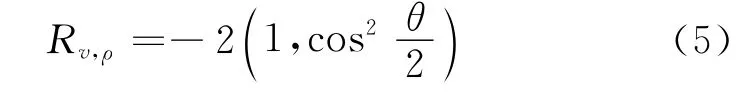
式中：θ為入射波方向與散射波方向的矢量夾角（開角）；Rv，ρ為速度、密度輻射模式，表示介質單點擾動對應的散射波能量與入射、散射角度的關系，其物理意義為，當一束平面波傳播至反射/散射體并發生反射/散射，其散射波場能量與開角的關系。

由速度、密度輻射模式可見：①速度輻射模式（圖1黑線）為一標準的圓形，物理意義是地下某一速度異常體擾動引起的波場擾動在各個方向上的振幅相同；②由地下某一密度異常體擾動引起的波場擾動能量只集中在小炮檢距處，其振幅隨著反射角的增大而減小（圖1紅線）；③在小炮檢距范圍內，速度輻射模式、密度輻射模式引起的波場擾動能量相近，耦合性很強，依靠小入射角地震數據難以區分速度和密度，同時密度貢獻主要集中在小炮檢距。因此在速度—密度參數化模式下，速度、密度之間的耦合性不可避免。圖2為速度、密度中心擾動介質散射波場。由圖可見，二者的擾動波場振幅在小入射角時基本相同，密度擾動引起擾動波場振幅隨著散射角增大逐漸衰減（圖2b），這與圖1的分析結果一致。

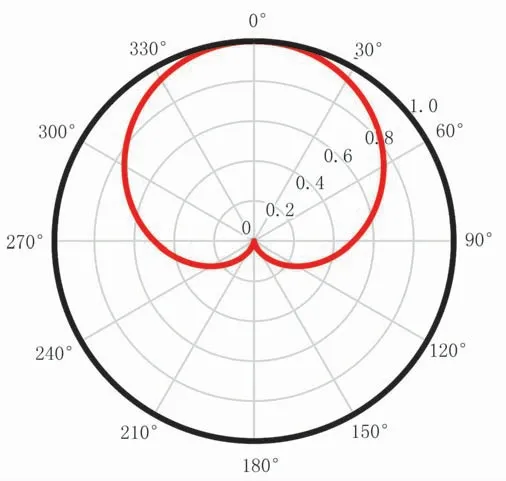
圖1 速度、密度輻射模式

圖3為密度擾動下的散射波場振幅隨炮檢距變化。由圖可見：當炮檢距較大時，檢波點位于次能量區域，即檢波點無法接收有效的散射信息（圖3a）；當炮檢距較小時，散射波集中在主能量區域，此時密度擾動對散射波形影響極大，因此密度FWI主要依賴于小入射角反射/散射波（圖3b）。圖4為密度擾動介質散射波記錄。由圖可見，密度擾動引起的散射波能量隨炮檢距增大而減小，在遠炮檢距處振幅逐漸趨近于零，說明密度FWI只依賴于小入射角反射波。眾所周知，大炮檢距波形包含了豐富的折射波和潛水波信息，大炮檢距數據驅動可為波形反演提供大尺度背景信息。因此僅僅依賴中、小炮檢距信息的密度反演結果主要為高波數成分，類似于偏移剖面。

圖2 速度（a）、密度（b）中心擾動介質散射波場

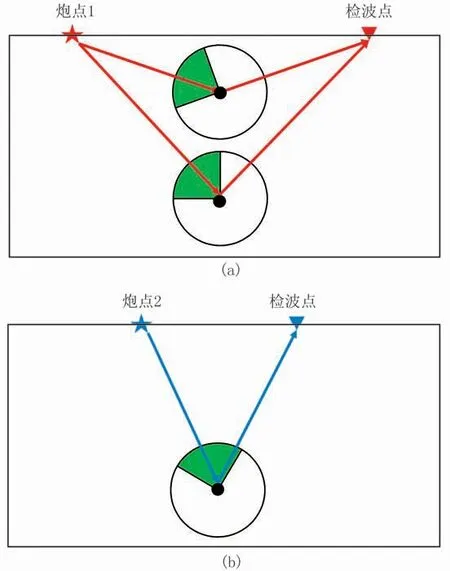
圖3 密度擾動下的散射波場振幅隨炮檢距變化

圖4 密度擾動介質散射波記錄

1.1.2 頻率因素

在有限炮檢距情況下，恢復模型波數同樣受頻率影響，其直接表現為第一菲涅耳帶寬度［33］。

Sirgue等［34］指出，地震波的低頻對應于模型的低波數，二者呈線性關系。鑒于此，Jeong等［5］在頻率域利用超低頻信息（0.167Hz）擴大第一菲涅耳帶的縱向范圍恢復完整的低波數信息，最終通過多尺度反演得到精確的密度模型，但由于地震采集因素的限制，無法投入實際應用。當縱向深度小于或接近第一菲涅耳帶半徑時，密度敏感核仍然由低波數主導，雖然在垂直于波傳播方向上密度敏感核振幅很小，但可在步長尋優過程中得到補償，低波數更新量仍然可觀。在時間域反演的梯度計算過程中，由于低頻信息被梯度表達式中的懲罰函數［35］壓制，仍難以恢復低波數。

1.2 互相關RWI

由前文可知，傳統密度波形反演只依賴于中、小炮檢距的反射波數據，只能恢復模型的高波數成分。若要恢復低波數成分，只能依賴于RWI［14］。由于RWI方法主要反演大尺度背景模型而不考慮模型的擾動量，因此可以看作連續介質反演。針對模型的大尺度背景，依據Gadrner公式［36］

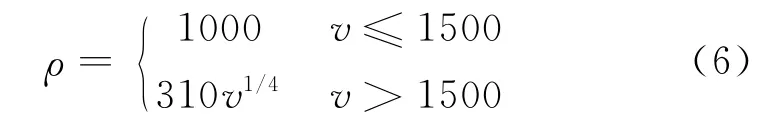
同時反演兩個參數。因此，文中以速度反演為主，通過式（6）更新密度。

根據式（4）得到速度敏感核函數

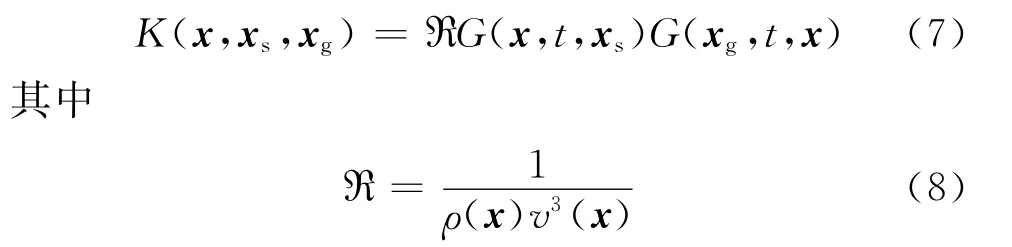
沿著敏感核（波路徑）反傳數據殘差同時更新速度模型的低波數和高波數成分，為了區分不同波場數據（直達波/潛水波和反射波等）對模型參數的貢獻量，將當前FWI敏感核分解為

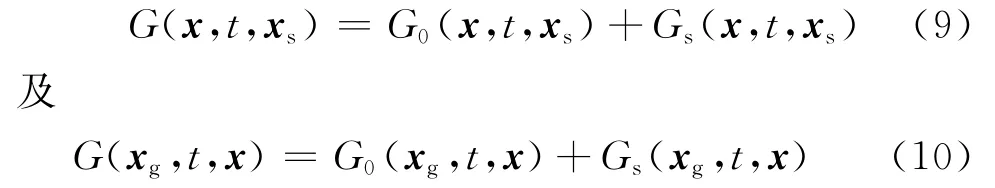
式中：G0為背景介質的Green函數；Gs為擾動介質的Green函數，文中對應反射波。將式（9）和式（10）代入式（7）得

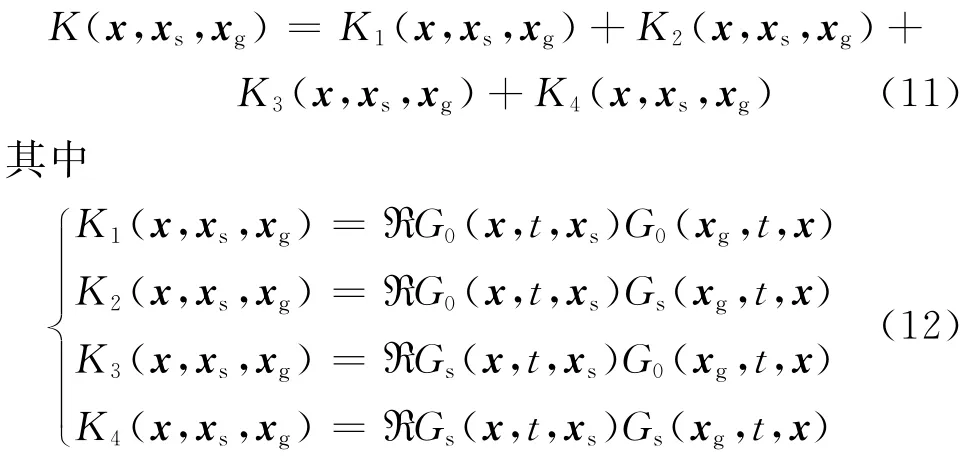
上述敏感核函數分解與傳統全波場敏感核函數（式（7））相比，K1（x，xs，xg）表示炮點正傳過程的入射波場與檢波點反傳過程的入射波場做零延遲互相關；K2（x，xs，xg）表示炮點正傳過程的入射波場與檢波點反傳過程的反射（散射）波場做零延遲互相關；K3（x，xs，xg）表示炮點正傳過程的反射（散射）波場與檢波點反傳過程的入射波場做零延遲互相關；K4（x，xs，xg）表示炮點正傳過程的反射（散射）波場與檢波點反傳過程的反射（散射）波場做零延遲互相關。不同子核有相應的物理意義（圖5）。

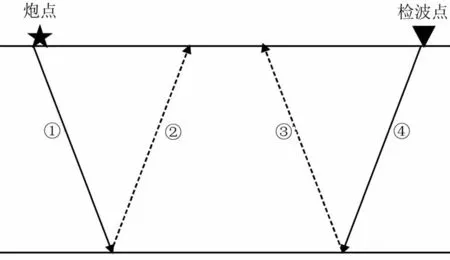
圖5 不同子核物理意義

Xu等［14］提出RWI策略，通過真振幅逆時偏移［15］/反偏移思想構建反射能量，利用反射能量恢復模型深部背景速度，在一定程度上克服了反演極易落入局部極值的現象。這里給出反射核函數

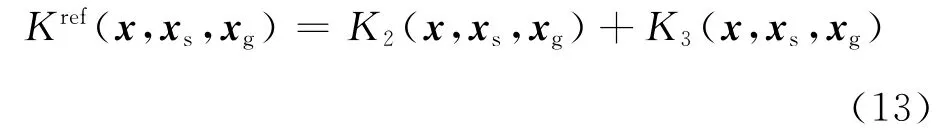
根據Gadrner公式建立目標函數的速度—密度梯度

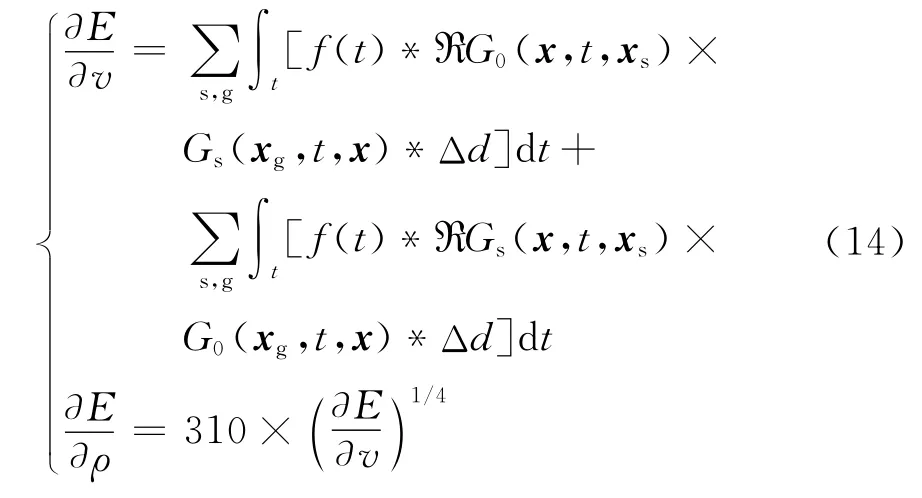
式（14）包含正向背景波場G0（x，t，xs）、正向散射波場Gs（x，t，xs）、背向背景波場G0（xg，t，x）和背向散射波場Gs（xg，t，x），通過偏移/反偏移獲得散射波場［10］。

在最小二乘目標函數下的波形反演方法中，為了得到真振幅正向和背向散射波場，在常規反演迭代循環中，每更新一次模型參數，都要額外增加一次最小二乘逆時偏移運算，因此其計算量遠遠超過傳統波形反演。因此本文采用互相關目標函數替代傳統的最小二乘目標函數，以避免每次迭代循環中由最小二乘逆時偏移帶來的海量計算量。

重新定義觀測記錄與反偏移記錄的互相關算子

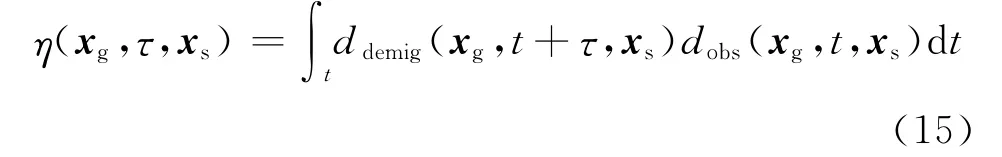
式中ddemig為反偏移記錄，τ為時移量。考慮模擬記錄與觀測記錄之間可能存在相位差異，選取以下目標函數［37］

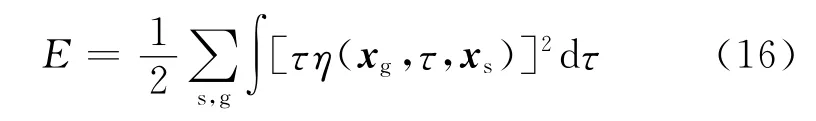
則速度模型參數的梯度為［21］

Wang等［21］將上式定義為旅行時項和Born項兩部分，其中旅行時項不僅反映數據振幅誤差的影響，同時能夠更新模型低波數分量，因此采用旅行時項作為梯度而忽略Born項。因此速度、密度梯度為如下Green函數形式

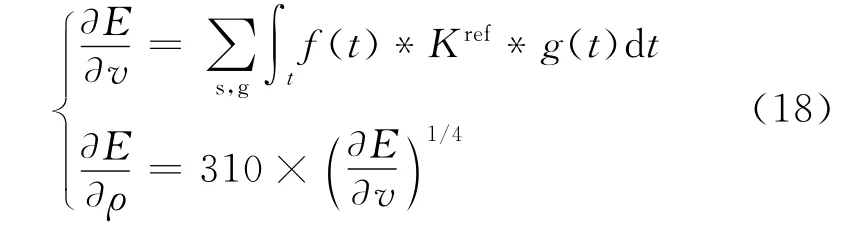
式中g（t）為反傳虛震源。基于波動方程的反演方法需要建立散射體和散射波場的線性關系（非線性關系求解難度較大），相應發展了Born近似和Rytov近似等方法。Born近似反映了速度擾動和波場擾動的線性關系，并綜合考慮了振幅、相位等因素。Rytov近似反映了速度和波場相位的關系，反演的線性程度較Born近似更明顯。為增強反演線性化，Luo等［19］基于Rytov近似，通過對數域波場分離振幅和相位，推出新的虛震源形式

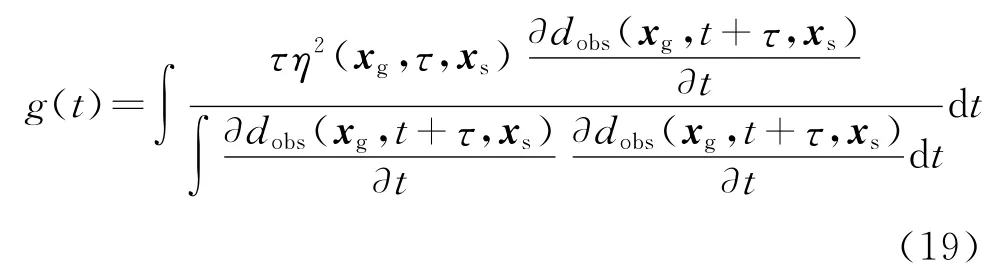
最后結合式（3）進行速度—密度雙參數反演，在速度—密度同步反演迭代過程中，由該輪次迭代的速度更新量通過式（6）得到密度更新量，最終完成速度和密度低波數模型重建。需要指出，基于互相關目標函數的RWI必須同時反演密度和速度，因為大尺度密度背景差異不會改變地震波走時，走時信息僅依賴于背景速度。因此本文提出的互相關RWI是利用密度與速度的高度耦合性重建密度反演的低波數成分。表1為基于RWI＋FWI的速度—密度雙參數反演流程。

表1 基于RWI＋FWI的速度—密度雙參數反演流程

2 數值模擬結果及分析

2.1 雙層模型

采用各向同性介質雙層模型進行測試。首先分析傳統FWI對于速度和密度模型的低波數反演能力，此處修正的上層速度和密度參數分別為2700m/s和1200kg/m3，得到背景速度、密度模型。由于主要沿著反射波路徑更新低波數能量，而平滑模型造成正傳、反傳波場在彈性界面不產生反射（散射），進而引起迭代初期只更新界面、反射波路徑能量在迭代多次才出現增強的現象，因此未對背景模型平滑處理。圖6為第1次迭代的FWI速度梯度與密度梯度剖面。由圖可見：在速度梯度剖面中反射波路徑低波數能量很強，呈2個“兔耳”形態，說明反射波數據具備恢復速度殘差模型（真實模型速度與初始模型速度的差值）低波數分量的能力（圖6a）；在密度梯度剖面中幾乎觀察不到“兔耳”形態，意味著反射波數據無法恢復密度殘差模型低波數信息（圖6b）。在放棄以潛水波和折射波數據驅動的大尺度密度模型反演后，由反射波數據無法恢復低波數成分，這對于成功反演各尺度密度模型非常不利。

在速度RWI的同時，利用Gardner公式更新密度模型，因為RWI存在偏移/反偏移過程，無需初始模型提供界面信息，因此將初始速度和初始密度設置為參數統一的均勻模型，文中分別設置速度為3300m/s、密度為1800kg/m3和速度為2700m/s、密度為1200kg/m3兩套參數。圖7為RWI單炮高、低密度梯度模型。由圖可見，高、低密度梯度均僅存在沿著反射波路徑的低頻能量，并對應密度模型的低波數成分，同時正確指示了背景參數的偏高或偏低方向。圖8為RWI 20炮疊加高、低密度梯度平滑模型。由圖可見，本文提出的反演策略有效恢復了密度低波數成分。

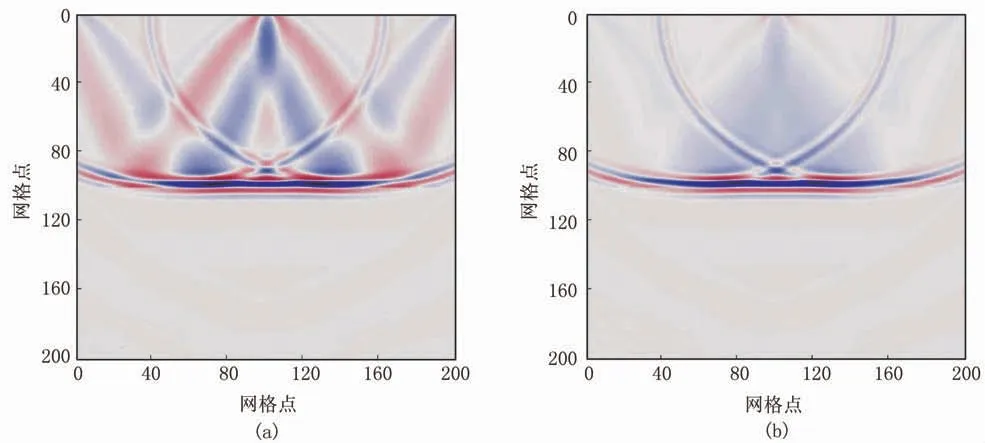
圖6 第1次迭代的FWI速度梯度（a）與密度梯度（b）剖面

圖7 RWI單炮高（a）、低（b）密度梯度模型

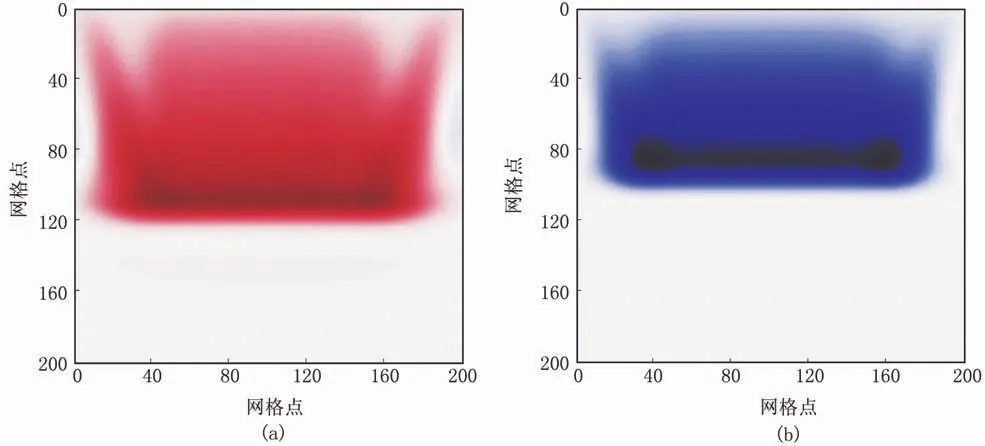
圖8 RWI 20炮疊加高（a）、低（b）密度梯度平滑模型

2.2 Sigsbee 2A模型

采用Sigsbee 2A重采樣模型（圖9）進行數值試算。首先用初始線性速度（圖9c）、初始線性密度（圖9d）模型進行傳統FWI測試，測試結果（圖10、圖11）表明：①初次迭代的密度梯度（圖10b）的高波數較速度梯度（圖10a）更明顯。②迭代18次后陷入局部極值，雖然能看出構造輪廓，但是速度反演結果嚴重偏離真實模型（圖9a），整體地層界面明顯下移，繞射點歸位不好，存在“畫弧”現象（圖11a）；密度反演效果更差，僅更新了錯誤的高波數信息（圖11b）。

采用本文提出的速度—密度同步RWI方法重新迭代、更新初始速度、密度模型（共迭代39次），圖12為速度—密度同步RWI初次迭代、第20次迭代的密度梯度疊加剖面。由圖可見：RWI初次迭代的密度梯度（圖12a）的能量主要集中在淺層，較傳統FWI密度梯度（圖10b）更光滑，低波數能量更豐富；RWI迭代第20次的密度梯度（圖12b）的能量逐漸向中、深部轉移，并且伴隨著一些高波數信息（界面處）。由于RWI主要是為了提供殘差模型的低波數信息，以修正地震波走時（針對速度而言）、相位等，人們一般在迭代中對梯度做適當平滑以消除界面能量，使模型更新主要以低波數為主。因此，在速度—密度雙參數RWI中，文中對每次迭代的梯度均做輕微高斯平滑。最終反演結果（圖13）表明，與初始線性模型（圖9c、圖9d）相比，RWI最終結果明顯存在低波數成分。

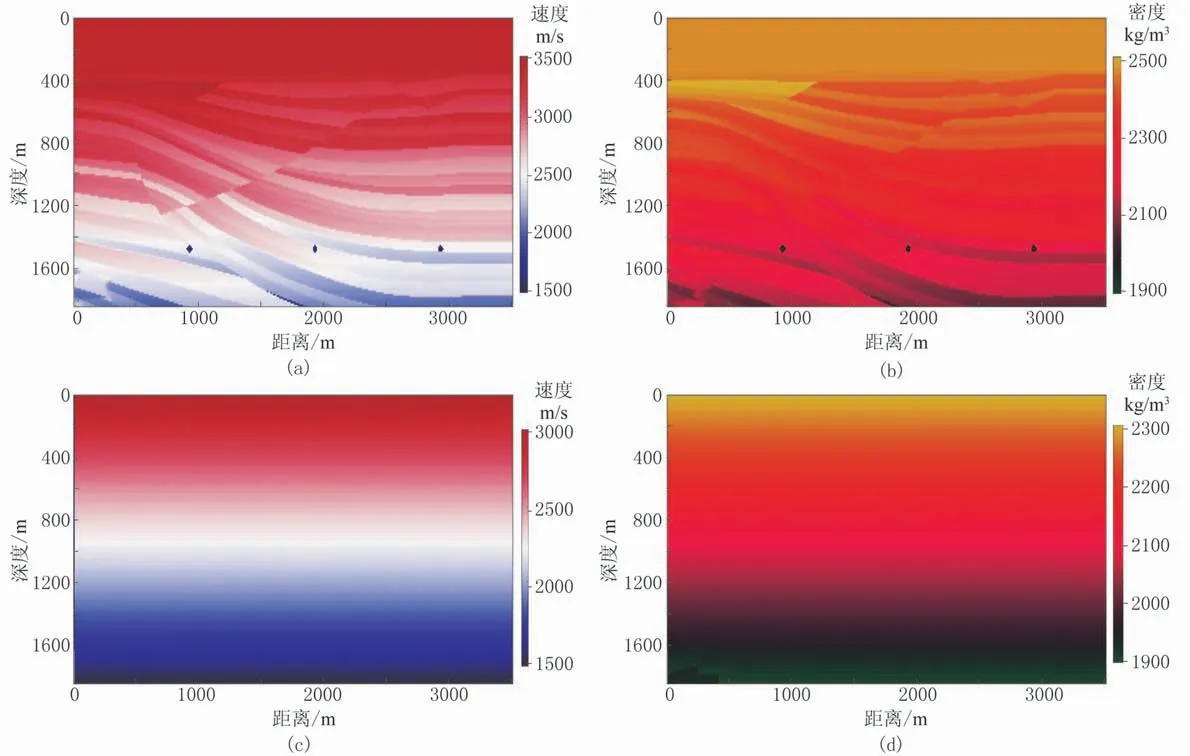
圖9 Sigsbee 2A重采樣模型

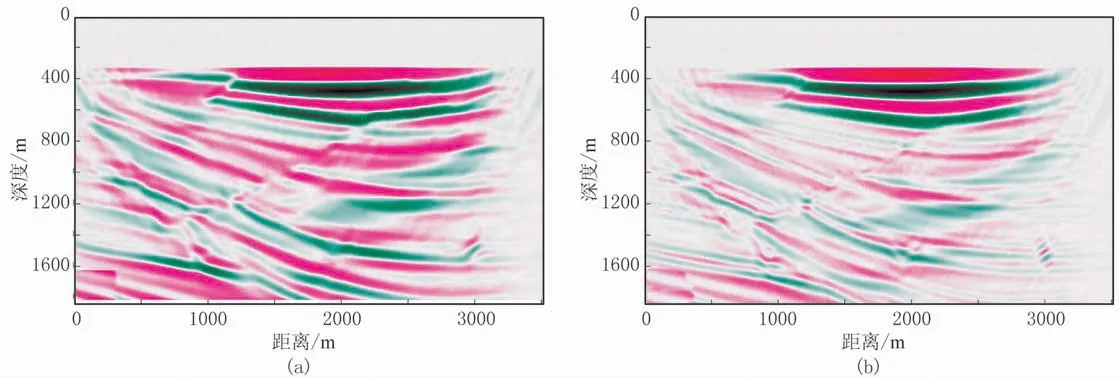
圖10 傳統FWI初次迭代的速度（a）、密度（b）梯度疊加剖面

圖11 傳統FWI迭代18次的速度（a）、密度（b）結果

圖12 速度—密度同步RWI初次迭代（a）、第20次迭代（b）的密度梯度疊加剖面

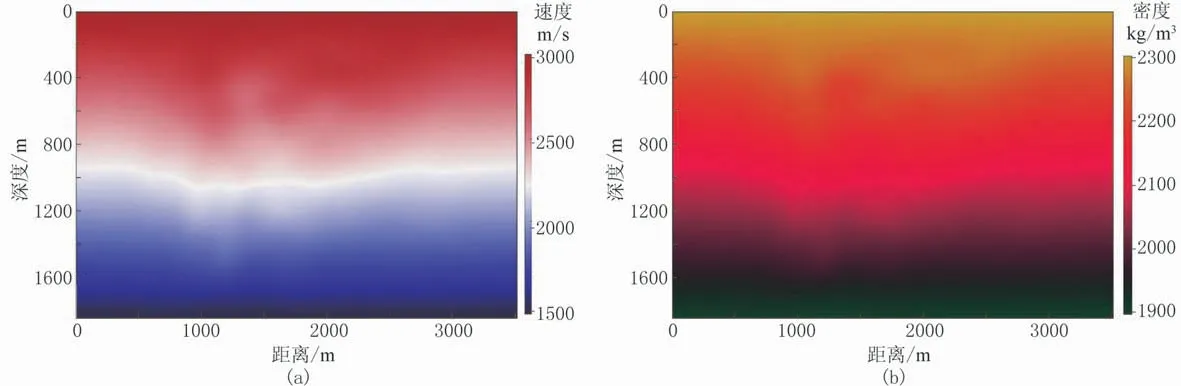
圖13 Sigsbee 2A模型最終RWI速度（a）、密度（b）

圖14 Sigsbee 2A模型RWI＋FWI迭代39次的速度（a）、密度（b）

為檢驗RWI更新的低波數信息的準確性，在RWI速度、密度基礎上，再次進行傳統FWI測試，圖14為Sigsbee 2A模型RWI＋FWI迭代39次的速度、密度。由圖可見，速度（圖14a）和密度（圖14b）反演結果中層位清晰，繞射點準確歸位并且沒有繞射“畫弧”現象。抽取真實速度（圖9a）、初始線性速度（圖9c）、傳統FWI迭代18次的速度（圖11a）、RWI速度（圖13a）以及RWI＋FWI迭代39次的速度（圖14a）在水平方向1.0、1.5、2.0、2.5、3.0km處的縱向曲線（圖15）可見：①由于初始線性速度與真實速度差異較大，傳統FWI迭代18次的速度存在嚴重周波跳躍，導致反演很早落入局部極值，并且速度模型的更新也集中在初始線性速度附近，嚴重偏離真實值。②RWI速度明顯接近真實速度，說明RWI提供了準確的低波數更新量，因此RWI＋FWI速度基本與真實速度吻合，僅在深部（深度大于1.6km）與初始線性速度相近，這是由于模型深層無有效反射信息導致RWI速度不精確所致。抽取真實密度（圖9b）、初始線性密度（圖9d）、傳統FWI迭代18次的密度（圖11b）、RWI密度（圖13b）以及RWI＋FWI迭代39次的密度（圖14b）在水平方向1.0、1.5、2.0、2.5、3.0km處的縱向曲線（圖16）進行分析，結果與速度分析結果基本一致，由于密度反演固有的偏移特性，RWI為密度提供了唯一的低波數信息，加強了密度反演的層析特征，因此反演結果更準確。

圖15 真實速度（黑色實線）、初始線性速度（黑色虛線）、傳統FWI迭代18次的速度（紅色實線）、RWI速度（粉色實線）以及RWI＋FWI迭代39次的速度（藍色實線）在水平方向1.0（a）、1.5（b）、2.0（c）、2.5（d）、3.0km（e）處的縱向曲線

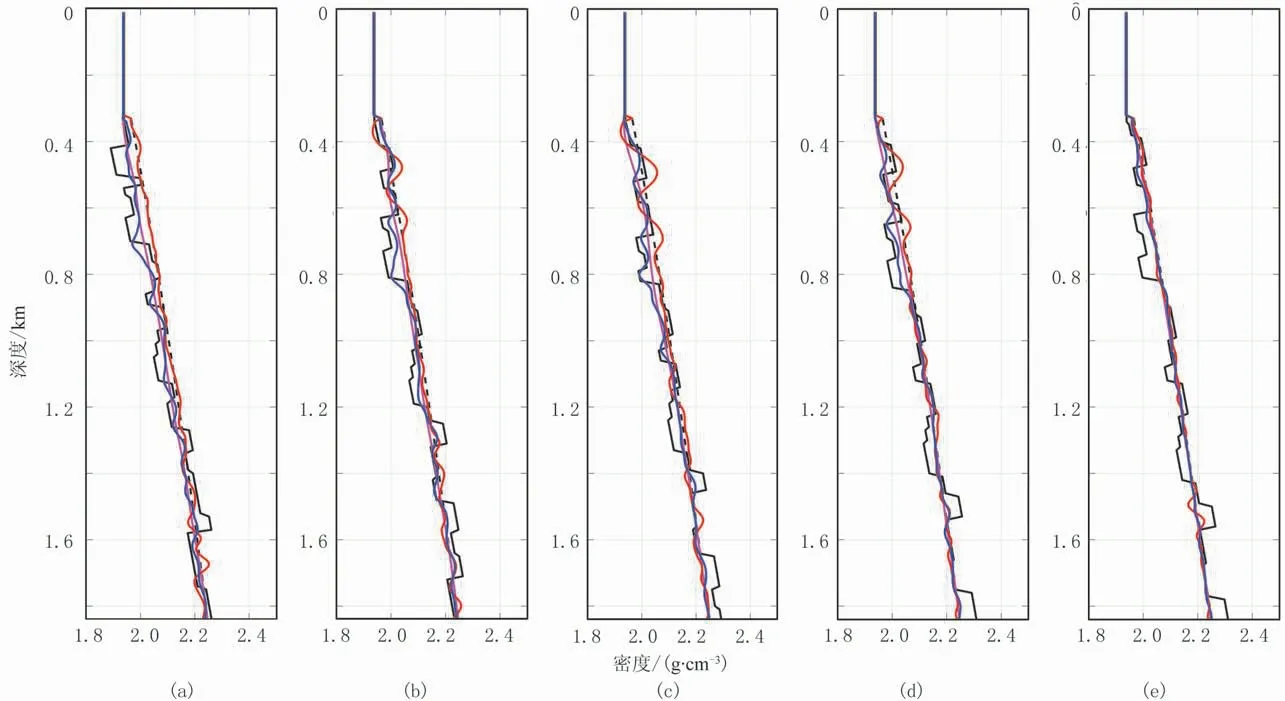
圖16 真實密度（黑色實線）、初始線性密度（黑色虛線）、傳統FWI迭代18次的密度（紅色實線）、RWI密度（粉色實線）以及RWI＋FWI迭代39次的密度（藍色實線）在水平方向1.0（a）、1.5（b）、2.0（c）、2.5（d）、3.0km（e）處的縱向曲線

3 結論

速度和密度雙參數同時反演是目前相對有效的密度反演參數化模式，而二者之間的耦合性給傳統FWI帶來巨大挑戰。此外，密度FWI還存在強偏移效應的問題，即傳統FWI密度反演結果的層析分量嚴重不足。為此，本文提出了基于互相關目標函數的速度—密度雙參數RWI方法，然后對RWI結果利用傳統FWI最終得到較準確的速度、密度反演結果。通過理論分析和模型測試得到以下認識：

（1）密度擾動對大炮檢距信息的敏感性很低，因此只能利用中、小炮檢距的地震反射數據反演密度，而小炮檢距數據的密度反演結果的低波數成分嚴重缺失，進而導致同時反演陷入局部極值。此外，實際生產中還面臨低頻缺失、子波帶限、觀測孔徑等問題，極易導致反演失敗。RWI可克服反演局部極值以及減弱密度偏移特征。

（2）速度、密度參數之間的強耦合效應（更新速度的同時根據經驗公式同時更新密度）是大尺度背景模型RWI的理論基礎。在實施RWI過程中利用Gardner經驗公式同時對速度和密度進行更新，最終可精確地恢復速度、密度的低波數信息。