基于FCM聚類算法的自適應逆控制器設計

明 飛

（上海電氣電站工程公司）

自適應逆控制的關鍵在于被控對象逆模型的建立，在實際中，絕大部分情況下無法得到被控對象精確的數學模型。 很多情況下，采用一些智能計算方法可得到被控對象的逆模型， 例如Volterra 基 函 數 網 絡［1，2］、神 經 網 絡［3，4］及 模 糊 系統［5，6］等。

T-S模糊模型由一組if-then規則來建立，其后件部分是一線性等式，被廣泛應用于非線性系統的建模與控制。T-S模糊模型應用于自適應逆控制器的基本思路為： 首先根據試驗得到輸入-輸出訓練數據，然后在訓練數據的基礎上進行結構辨識和參數辨識。 結構辨識一般包括輸入變量的選擇、輸入變量空間的劃分等，輸入變量的選擇一般根據運行經驗或者專家知識等進行，輸入空間的劃分方法包括網格法、模糊數法及模糊聚類算法等。 完成T-S模糊模型的結構辨識后，在此基礎上進行T-S模糊模型的參數辨識，參數辨識包括前件參數辨識和后件參數辨識。

模糊C均值（Fuzzy C-means，FCM）聚類算法是一種無監督學習算法，常應用于T-S模糊前件參數的辨識。 FCM聚類算法不需要先驗知識，直接根據訓練數據得到模糊系統的前件部分。 定義了聚類的個數即對應了模糊系統的規則數，可避免模糊系統的規則爆炸問題， 實施起來也較為簡單。 后件參數可以通過最小二乘算法或者正交最小二乘算法得出，最小二乘算法是一種較常使用的函數擬合算法，易于實現。

筆者提出一種基于FCM聚類算法的自適應逆控制器設計算法，并通過兩個非線性對象的仿真試驗驗證筆者提出的控制器的控制效果。

1 FCM聚類算法

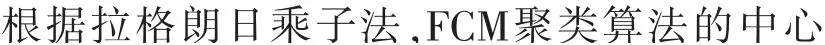
2 T-S模糊模型

T-S模糊模型的if-then規則描述為［7］：

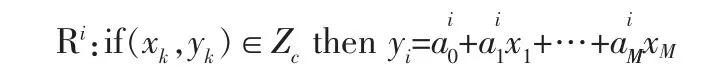
這里，樣本表示為（xk，yk）（k=1，2，…，N）。 通過FCM聚類算法，第i條規則的激發隸屬度即為數據通過FCM聚類算法得到的隸屬度。T-S模糊模型的輸出可表示為：

3 基于FCM聚類算法的模糊逆模型

3.1 前件參數辨識

前件參數通過FCM聚類算法得到，步驟為：

a. 根據系統輸入-輸出數據，生成N對以向量形式描述的訓練數據；

b. 對N對訓練數據進行聚類運算， 聚類算法結束以后得到c類中心；

c. 每一組訓練數據， 根據中心得到c個隸屬度，分別對應c條模糊規則的激發隸屬度。

3.2 后件參數辨識

在前件參數的基礎上，本項目T-S模糊模型的后件參數通過最小二乘（Least Squares，LS）算法計算。 LS算法通過最小化誤差的平方和尋找數據的最佳函數匹配。 利用最小二乘法可以簡便地求得未知的數據，并使得這些求得的數據與實際數據之間誤差的平方和最小。

根據LS算法，P的最小二乘估計為：

其中，X是根據T-S模糊模型前件參數和輸入變量組合得到的一組向量，Y為系統的輸出向量。

LS算法有個缺陷就是需要矩陣X是可逆的，這在實際過程中不一定能完全滿足，為了避免矩陣求逆，可以采用遞推最小二乘算法。 設X的第i個行向量為，Y的第i個分量為Yi，則遞推最小二乘算法為：

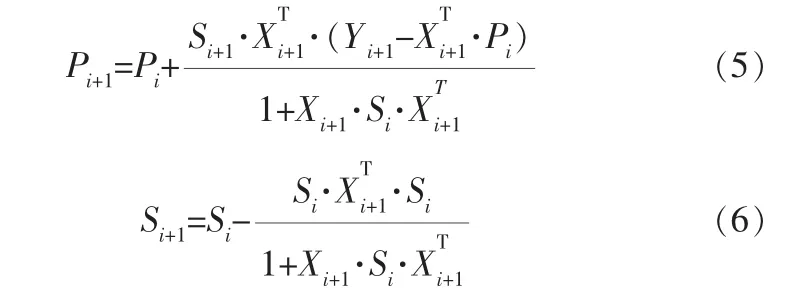
初始條件P0=0，S0=αI。 α一般取大于10 000的實數，I是L×L的單位矩陣，L=（M+1）c，M是T-S模糊模型的輸入變量個數，c是T-S模糊模型的規則數目。

4 自適應逆控制器

自適應逆控制器的基本思想是用被控對象的逆作為串聯控制器來對系統的動態特性進行開環控制，從而避免了因反饋閉環而引起的不穩定問題，同時又能做到對系統動態特性的控制與對象擾動的控制分開處理而互不影響。 與傳統的控制類似，自適應逆控制的最終目的是使得系統設定值和系統輸出值的偏差最小。

自適應逆控制器的一般結構如圖1所示［8］。

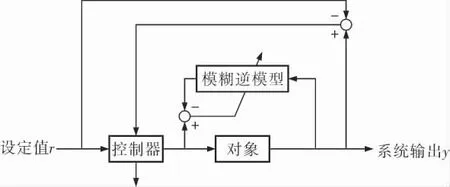
圖1 自適應逆控制器的一般結構

自適應逆控制器的第1步是建立模糊逆模型。 本項目的模糊逆模型采用T-S模糊模型，其最終模型參數使得模糊逆模型的輸出和實際輸出的偏差最小，也即模糊逆模型盡可能地擬合實際對象。 自適應逆控制的輸入是設定值和對象前幾個時刻的輸入或者輸出，具體的輸入變量根據實際對象特性選擇。 控制器的參數通過設定值和系統輸出的偏差來調整， 調整算法基于最小均方（Least Mean Square，LMS）算法。 這里的模糊逆模型是通過前文描述的FCM聚類算法建立的。

LMS是一種高效的濾波算法［9］，是梯度下降法的一種改進，LMS算法無需輸入信號和期望信號的特征值， 計算簡單， 在平穩信號情況下收斂性好，在自適應控制中應用較為廣泛。 其計算式為：

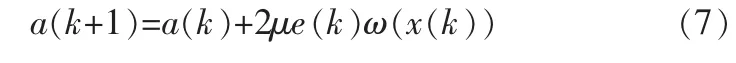
其中，a為T-S模糊模型的后件參數，自適應逆控制器的參數調整即是調整a；μ為學習步長，此處采用固定步長；e（k）為當前時刻設定值和系統輸出的誤差，e（k）=r-y（k）；ω（x（k））為包含了當前模型輸入和T-S模糊模型參數的一個表達式，即：

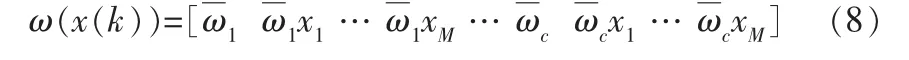
5 仿真實例

5.1 仿真實例1

本例選擇如下離散對象：

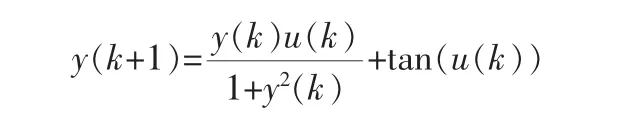
該對象正模型的輸入為y（k）和u（k），輸出為y（k+1）；逆模型的輸入為y（k）和y（k+1），逆模型的輸出為u（k）。 根據筆者提出的方法，利用FCM聚類算法建立該對象的逆模型。 首先在［-1，1］區間內產生均勻分布的隨機數作為系統輸入u（k），通過對象模型生成100組建立逆模型所需的輸入輸出對。 在實際中，訓練數據可根據現場運行數據得到。 本例所選擇的聚類個數（模糊規則數）為4。 設置系統的期望輸出r（k）=0.6sin（2kπ/250）+0.2sin（2kπ/250），圖2對比了筆者方法的輸出和期望輸出曲線，圖3為誤差曲線。 從圖2可以看出，兩條曲線基本上是重合的，說明系統輸出能夠很好地跟蹤設定值。 從圖3的誤差曲線也可以看出誤差很小，基本接近于零。

5.2 仿真實例2

本例選擇如下離散對象：

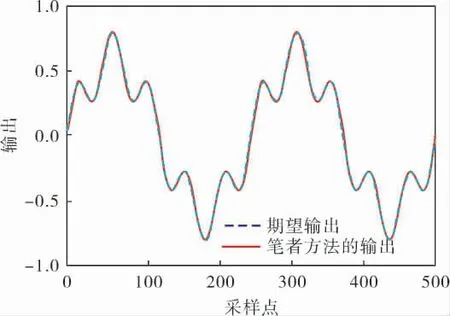
圖2 筆者方法和期望輸出曲線

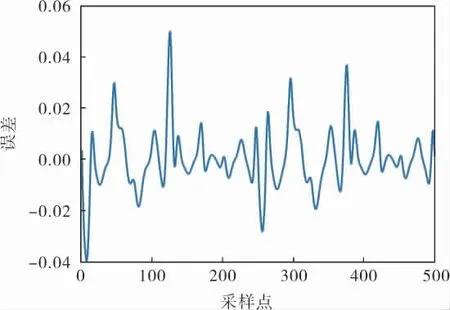
圖3 筆者方法和期望輸出誤差曲線

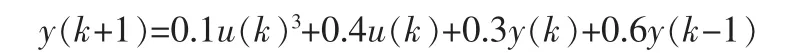
該 對 象 正 模 型 的 輸 入 為y（k）、y（k-1）和u（k），輸出為y（k+1）；逆模型的輸入為y（k-1）、y（k）和y（k+1），輸出為u（k）。 根據筆者提出的算法，利用FCM聚類算法建立該對象的逆模型。 首先在［-1，1］區間內產生均勻分布的隨機數作為系統輸入u（k），通過對象模型生成100組建立逆模型所需的輸入輸出對。 本例選擇的聚類個數（模糊規則數）為4。 假設系統的期望輸出r（k）=0.6sin（2kπ/250）+0.2sin（2kπ/250），圖4對比了筆者方法的輸出和期望輸出曲線，圖5為誤差曲線。從圖4可以看出，兩條曲線基本上是重合的。 從圖5的誤差曲線也可以看出， 系統輸出與設定值的誤差較小，基本接近于零。

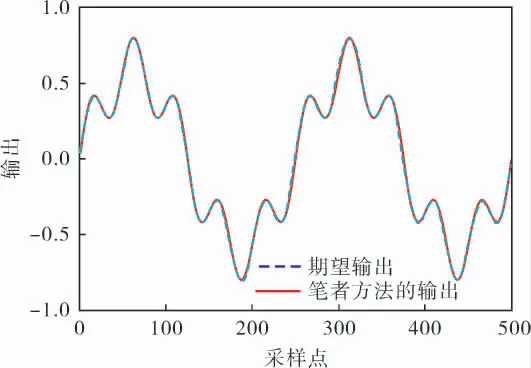
圖4 筆者方法和期望輸出曲線

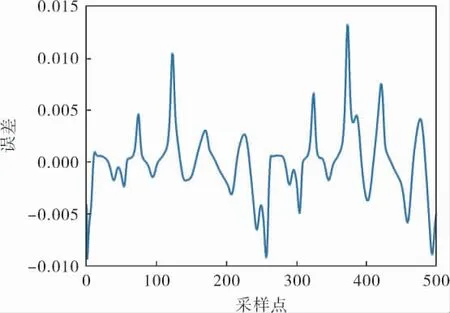
圖5 筆者方法和期望輸出誤差曲線

6 結束語

筆者提出了一種基于FCM聚類算法的自適應逆控制器設計算法。 首先利用FCM聚類算法建立對象的逆模型，FCM聚類算法建模簡單， 辨識前件參數數量較少且模糊規則的激發隸屬度求解簡單。 聚類結果即是模糊規則的激發隸屬度，不需要分別求取每個輸入變量的隸屬度，簡化了前件參數的辨識過程。 在逆模型的基礎上，設計自適應逆控制器，與被控對象串聯，使得系統的輸出能夠跟蹤設定值。 兩個非線性對象的仿真試驗表明：筆者提出的自適應逆控制器的系統輸出與設定值誤差較小，系統輸出基本上能夠立刻跟蹤上設定值，驗證了筆者提出的算法具有較好的控制效果。