安徽省礦點分布與主要形跡相關性的分形研究

施國棟,靳保路,陳 斌

(1.安徽建筑大學 土木工程學院,合肥 230601;2.建筑健康監測與災害預防技術國家地方聯合工程實驗室,合肥 230601;3.河海大學 地球科學與工程學院,南京 210098;4.浙江展圖建設有限公司,杭州 311600)

自1967年Mandelbrot首次提出分形概念,分形理論在研究非線性系統中得到了非常廣泛的應用,成為非線性學科的前沿,并應用于巖石學、工程地質、水系、地質災害、成礦規律、成礦預測等研究中[1-9],并成為地質礦產界在點和形跡研究領域的一場“革命”。礦點分布在宏觀上表現出雜亂無章,但是卻蘊藏著大量的分形現象,雜亂而有序,無章可定量[10-15]。分形理論不僅可以改變對礦點分布的傳統認識,而且對礦產資源預測有了全新的方法并產生重要影響。安徽省成礦地質條件優越,成礦模式、成礦規律和成礦系列劃分多樣,礦產資源分布呈現種類多、分布廣的特點,利用分形理論可以發現礦產資源總體分布的規律性,并將其與安徽省內主要形跡水系和斷裂的分形特征聯系起來,尋找分形聯系。

為了解決安徽省礦點分布與主要形跡相關性問題,首次將分形理論的方法應用于安徽省礦點分布的研究中,采用分形理論中的“盒維數法”對安徽省礦點分布的分形特征進行研究。以1∶50萬的安徽省礦點分布圖為底圖,進行矢量化處理和網格剖分,將安徽省區域劃分成256個子區域,計算出了每個小區域內的礦點分維值。同理， 計算出了每個小區域內的安徽省主要形跡水系和斷裂分維值,繪制其等值線圖,分析礦點分布與主要形跡的相關性。應用分形理論,在“雜亂無章”的礦點分布中研究其規律性及其與其他“雜亂”形跡的相關性,具有一定的現實意義和應用價值。

1 研究區概況

安徽省有著十分優越的地理條件,礦產資源豐富,為長三角地區發展提供了重要的礦產資源,是國家中部崛起戰略實施的重要發展區域,且礦產資源拉動著安徽省國民經濟高速發展。 截至2015年底, 已發現礦產158種(含亞種), 列入資源儲量表89種, 煤炭、 銅礦、 鐵礦是該省優勢礦產, 主要礦產分布呈“北煤、 中銅鐵、 南鎢”的空間格局, 全省查明資源儲量的固體礦產地1 437處, 其中大型礦床241處、中型礦床297處、小型礦床389處、小型以下礦產地510處。主要礦產資源在1∶50萬的安徽省礦點分布圖中標識礦點257處。2015年,全省礦石總產量4.65億t,采礦業產值798億元。全省規模以上礦山采選業及相關能源、礦產品加工制造業等礦業經濟總產值1.26萬億元,占全省工業總產值的31.64%[16]。

2 分形分維的引入

分形分維的測定目前經常采用的算法有碼尺法、自仿射分形法、冪律譜法、周長-面積關系法和盒維數法等5種方法。本文涉及不同尺度下的礦點和形跡線的統計分析,盒維數法在統計點線分維值方面準確直觀、操作性強,故采用該法。盒維數法又稱數格子法和網絡覆蓋法,即使用不同尺度的邊長為r的正方形網格(或稱之為盒子)去覆蓋所要計算的形跡底圖(邊長為L),分別計量在不同尺度下得到的盒子數N(r) 及分維值D[17-19]。

N(r)∝r-D,

(1)

(2)

分別以邊長為r=L/2、L/4、L/8、L/16和L/32的正方形網格覆蓋安徽省礦點圖和主要形跡圖, 統計在各尺度網格下有礦點和形跡的格子數N(r), 繪制成lnN(r)-lnr的散點圖, 根據式(1)、 (2), 利用最小二乘法對散點進行擬合分析, 擬合的直線斜率絕對值即為分維值D。若對任意的δ>0,N是能覆蓋S的最小網格數, 取不同大小的δ, log(1/δ)的值由小到大排列, 計算出不同的logN值, 再根據D=logN/log(1/δ)計算出記盒維數序列, 以log(1/δ)為橫軸、 logN為縱軸, 找出平面上點集的最佳逼近直線的斜率即為所求。

3 礦點分布與主要形跡相關性的分形

3.1 安徽省礦點分布分形特征

將安徽省1∶50萬礦產資源分布圖中的257個礦產資源分布點矢量化,以L=570 km為正方形底圖,然后劃分為2×2格(r=285 km)、 4×4格(r=142.5 km)、 8×8格(r=71.25 km)、 16×16格(r=35.625 km)和32×32格正方形(r=17.812 5 km), 依次統計出包含礦點的格子數N(r)(圖1、 表1), 以lnr為橫坐標、 lnN(r)為縱坐標, 用表1得到的5組數據, 擬合得安徽省礦點分形擬合方程為y=-1.337 1x+9.158 4, 故分維值D=1.337 1, 相關性系數R2=0.981 7(圖2), 分形相關性強, 表明安徽省整體礦點分布具有明顯的分形特征。 本文矢量化的安徽省礦點,雖然沒有區分圖中各個礦點之間的種類和成因區別,但是這種明顯的分形特征,又蘊含著同樣程度下種類的多樣性和成因的復雜性,說明礦點在安徽省區域內的分布是自相似的,而且局部分布與安徽省整體分布具有顯著的相似性。

圖1 安徽省礦點分形計算網格圖Fig.1 Grid of fractal calculation of ore spots in Anhui

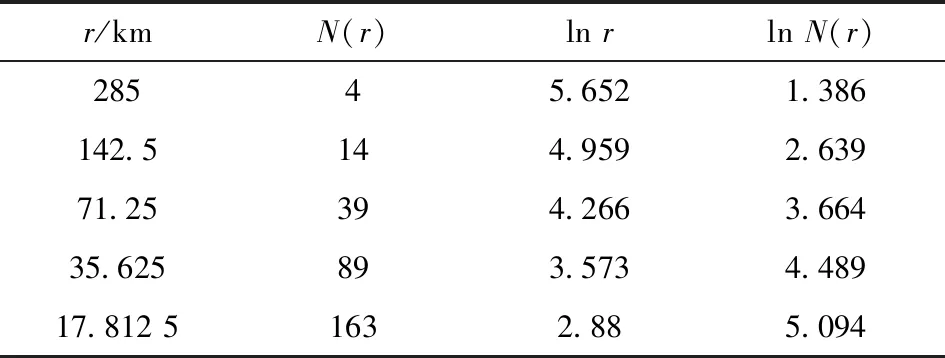
表1 安徽省礦點盒維數統計Table 1 Statistics of ore spots box dimension in Anhui

圖2 礦點分形擬合結果Fig.2 Fractal fitting results of ore spots

3.2 礦點分布與水系相關性的分形分析

礦點的分布與地質構造、巖石性質、地殼運動和巖漿活動等因素有關, 因此可從分布明顯的形跡水系和斷裂構造中尋找與礦點分布之間的關系。

同樣,運用盒維數法計算擬合方程得到安徽省總體水系(圖3)的分維值為1.582 5(表2),主要的水系淮河、長江和新安江,其分維值依次是1.383、1.331和1.02,表明水系的發育以淮河水系最復雜,長江水系次之,新安江最簡單且與淮河及長江水系分維值差值大。而三水系在安徽省內流域面積依次為6.69萬、6.6萬、0.65萬km2,這與實際的安徽省水系及三水系的分布發育整體情況一致。各水系的分維相關系數R2均大于0.9,表明各水系本身就具有顯著的分形特征,與Mandelbrot最初研究的英國海岸線的分形特征原理極為相似,分維值越高表明水系越發育的趨勢。通過對比本文的數據及他人對水系研究的數據,安徽省的水系分維值1.582 5,高于全國的的水系分維值1.418 9[20],表明安徽省的水系相對全國來說是非常發育的,這與安徽省內有淮河和長江兩大水系橫貫其中有關。

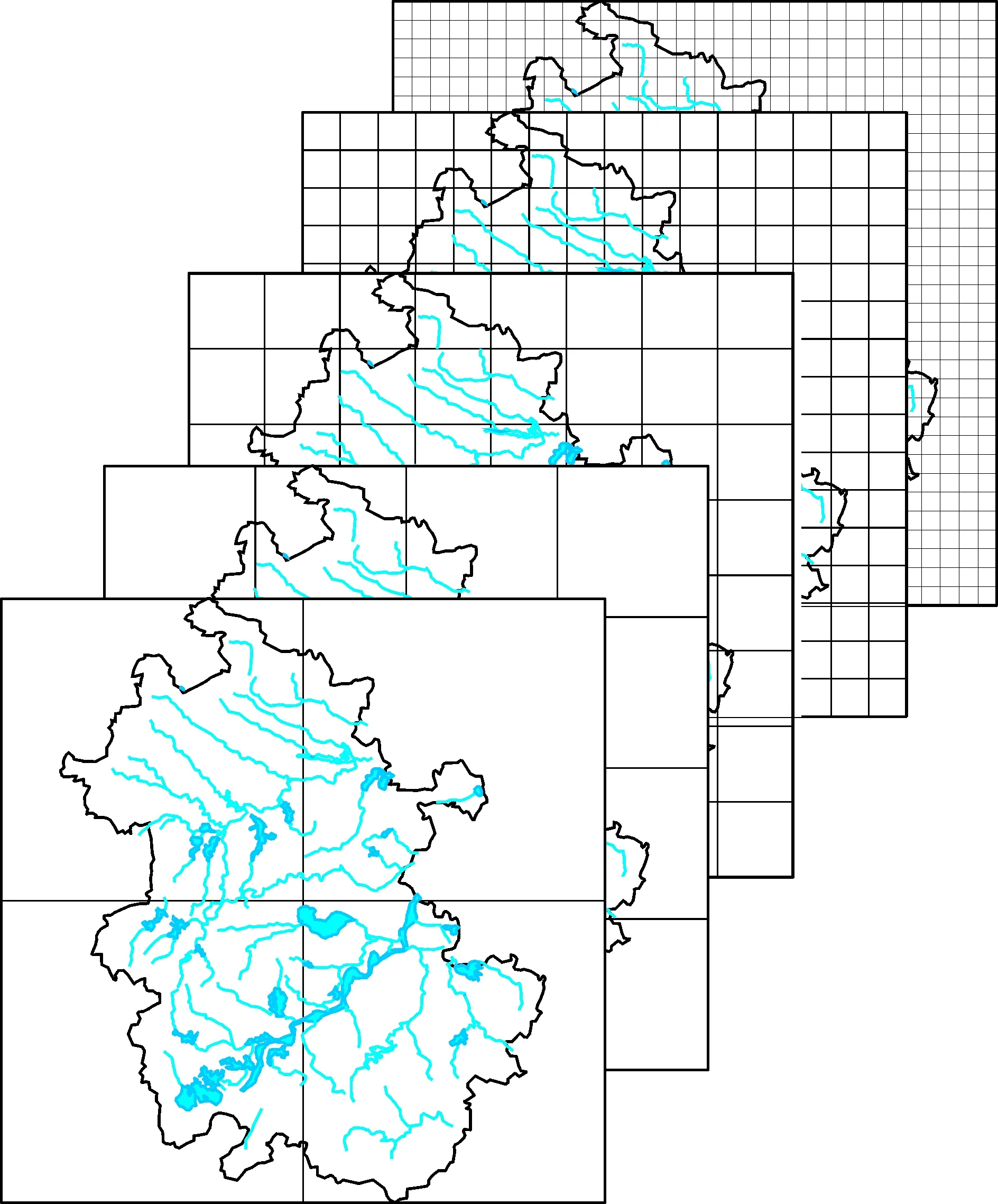
圖3 安徽省水系分形計算網格圖Fig.3 Grid of fractal calculation of water systems in Anhui

淮河水系發育復雜, 分維值最高(1.383), 包含礦點數86個; 長江水系分維值為1.331, 稍低于淮河, 包含礦點數卻為165個; 新安江水系發育最簡單, 分維值為1.02最低, 包含礦點數僅為6個。 說明安徽省境內水系的分維值與礦點的分布不是正比關系, 水系分維值在1.3左右(本文計算的分維值1.331, 朱曉華等計算的分維值為1.329 2[20], 孟憲萌等計算的分維值為1.386[22]), 礦點分布點數最多(表2)。 水系分維值可以反映水系所處流域地貌侵蝕發育程度和構造活動性的強弱[23], 而地貌侵蝕發育程度又與風化型礦產資源相關聯, 如長江水系所處地層中發育沉積型錳礦及其風化后形成的氧化錳礦, 強烈的河流地質作用, 又使得大量的礦產資源外露, 有色金屬礦產、 非金屬礦產相對集中。 安徽省礦產資源分布點的分維值1.337 1與長江水系的分維值1.331最接近, 表明安徽省的礦產資源分布受長江水系影響明顯, 且安徽省內分維值在1.3～1.4的水系有利于成礦。

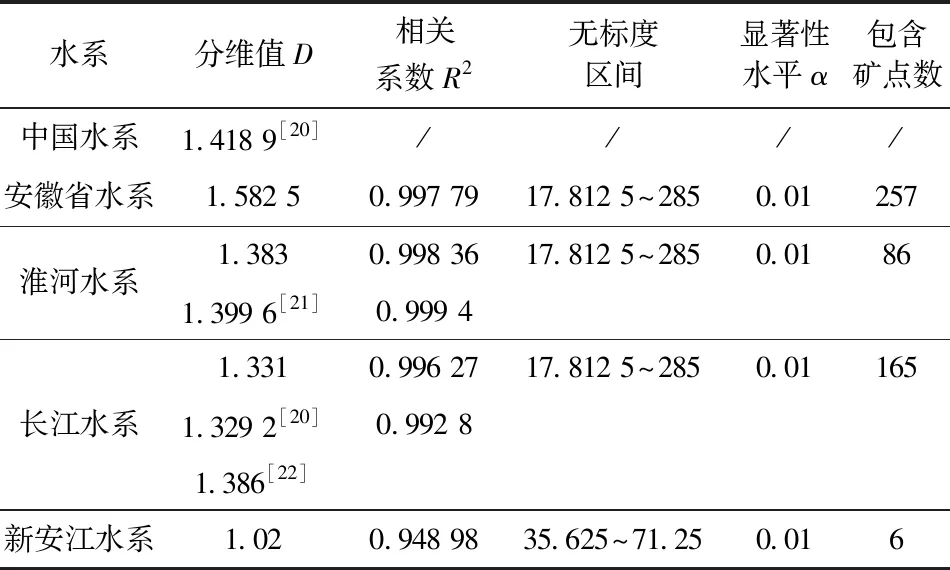
表2 主要水系空間分布分維值比較Table 2 Comparison of fractal dimension values of spatial distribution of main river systems

3.3 礦點分布與主要斷裂相關性的分形分析

同理,將斷裂底圖劃分為2×2、 4×4、 8×8、 16×16和32×32格正方形, 依次統計出包含礦點的格子數N(r)(圖4、 表3), 以lnr為橫坐標、 lnN(r)為縱坐標, 得到安徽省斷裂的分形擬合方程為y=-1.568 4x+10.338, 分維值D=1.568 4, 相關性系數R2=0.997 6(圖5), 相關性強, 具有顯著的分形特征。 安徽省斷裂分維值(1.568 4)大于礦產資源分布點分維值(1.337 1),故在此基礎上可對兩者的關系從分維角度作進一步的分析。

圖4 安徽省主要斷裂分形網格圖Fig.4 Fractal grid of main faults in Anhui

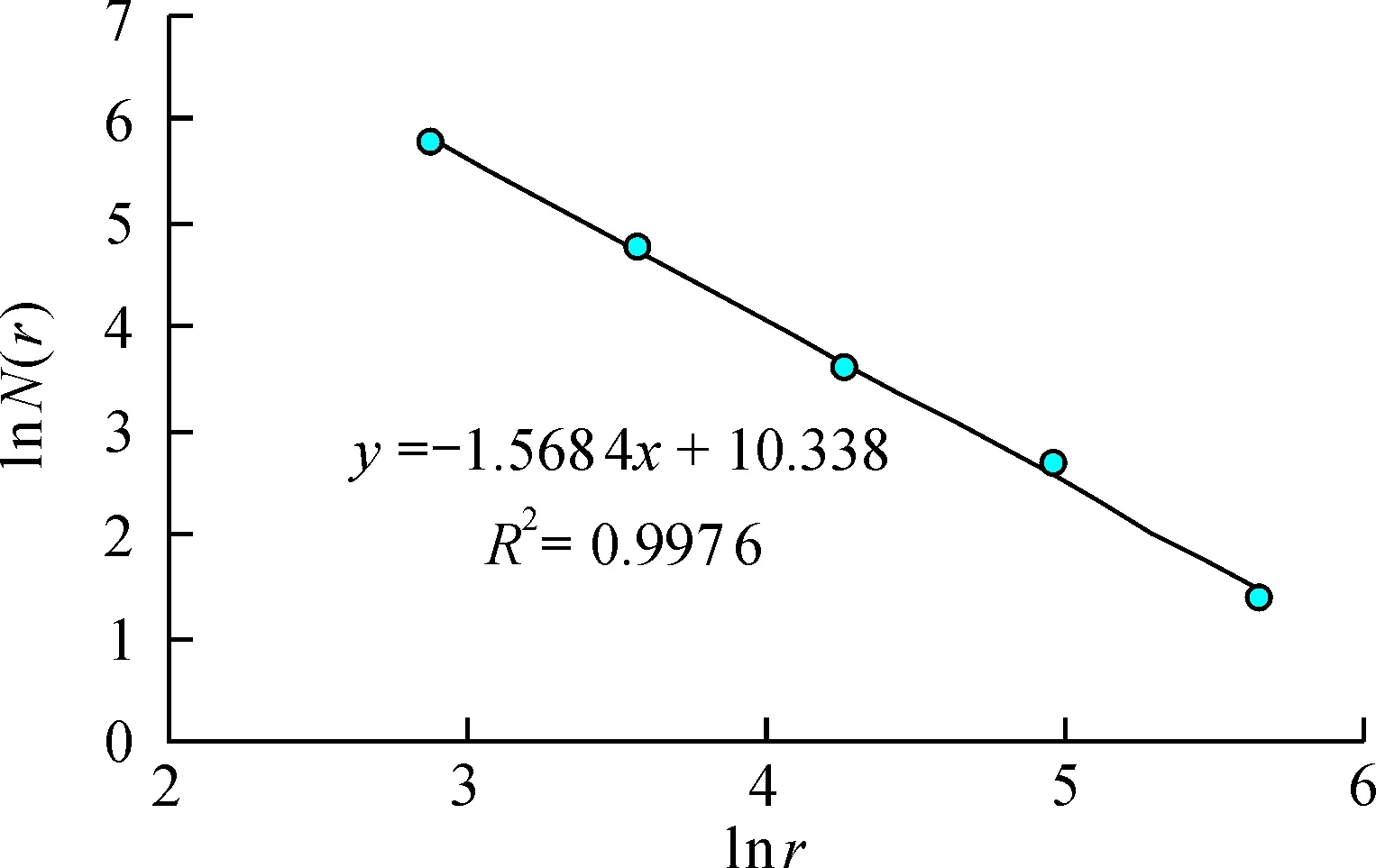
圖5 斷裂分形擬合結果Fig.5 Fractal fitting results of fracture

表3 安徽省主要斷裂構造盒維數統計Table 3 Statistis of box dimensions of major faults in Anhui

對斷裂形跡和礦點分布情況兩者都用盒維數法計算出各個分維值后,用16×16的小正方形覆蓋安徽省斷裂圖及礦點分布圖,將這256個區域的斷裂、礦點用盒維數法計算出各個分維值,將數據網格化導入到Surfer 軟件中作分維值的等值線圖,形成斷裂構造分維等值圖(圖6a)和礦點分維等值圖(圖6b)。 提取斷裂和礦點分布的分維值均大于1.0的等值線, 發現在安徽省內礦點分布形成了6個D≥1.0的獨立區域,且與斷裂分維值高值基本吻合。 安徽省斷裂分維值(1.568 4)與礦產資源分布點分維值(1.337 1)差異大, 表明安徽省內的礦產資源分布主要不是受斷裂控制的, 但是在高分維值區域,兩者之間又存在聯系。

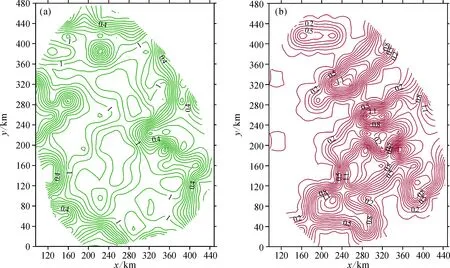
圖6 斷裂構造(a)及礦點(b)分維等值線圖Fig.6 Fractal contour of fault(a) and ore spot(b)

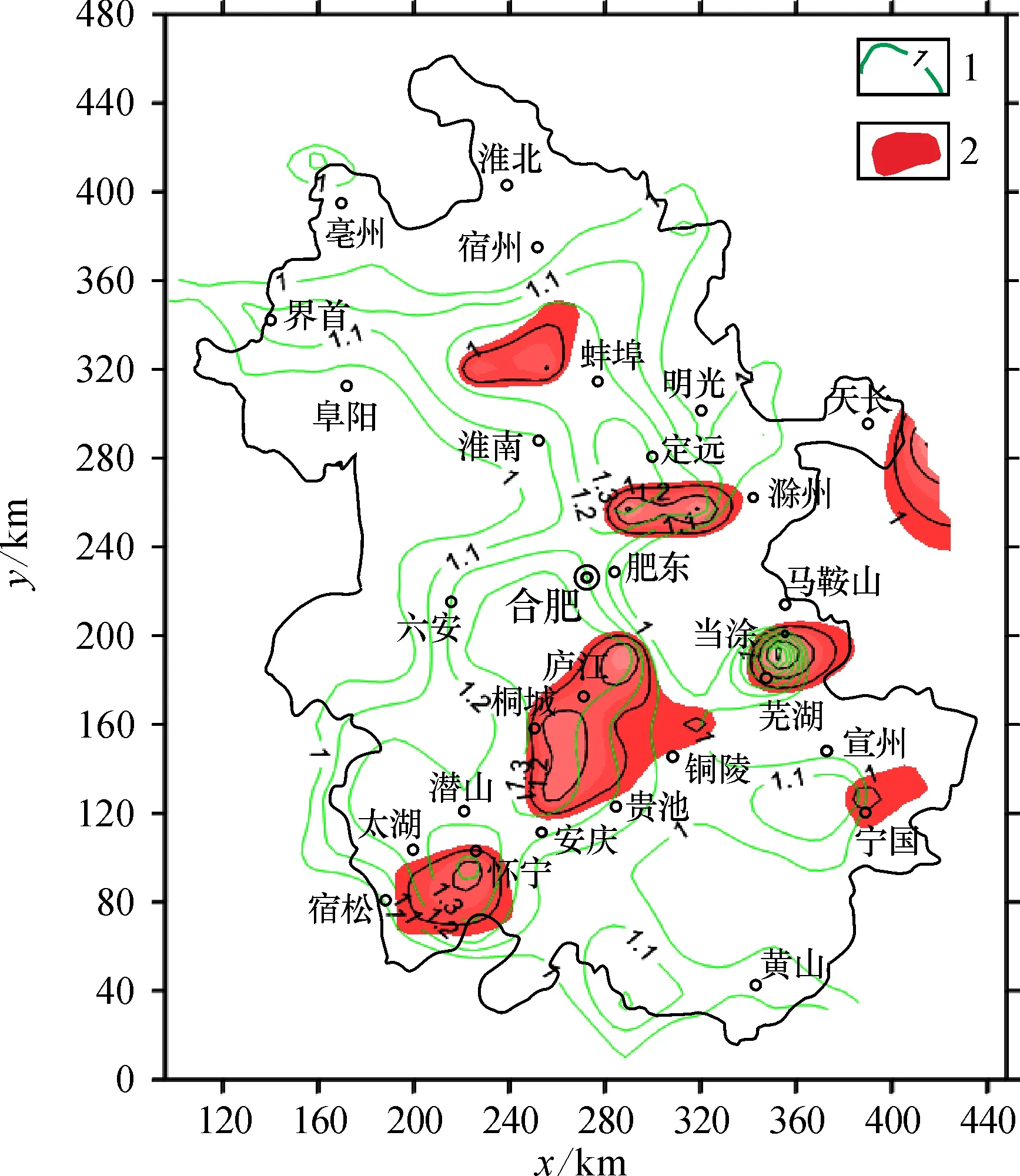
圖7 斷裂及礦點分維等值線(D≥1.0)疊加處理結果Fig.7 Superposition of fractal dimension isoline (D≥1.0) of faults and ore spots1—斷裂分維等值線; 2—高維疊加區

為了進一步揭示斷裂和礦點分布的關系, 在礦點分布分維值大于1.0的底圖中(圖7),將安徽省斷裂構造分維等值圖以D≥1.0、≥1.1、≥1.2、≥1.3和≥1.4作出5個層次圖,與礦點分布分維值進行關聯。通過Surfer 11計算上述5個范圍的分維區間下斷裂構造區域面積及其與礦點分布D≥1.0區域的重疊面積(表4、 圖8)。

圖8 斷裂構造不同分維值(D≥1.1、 1.2、 1.3、 1.4)等值線圖Fig.8 Contour maps of fault structures for different fractal dimension values(D≥1.1, 1.2, 1.3, 1.4)

表4 不同斷裂分維區間下礦點分布比例Table 4 Distribution proportion of ore spots under different fault fractal dimension intervals

由表4、圖9可知,隨著斷裂構造分維值增大,分維值覆蓋區域的不斷縮小,其斷裂分維所覆蓋的面積與礦點分布(D≥1.0)面積的比率越大； 在D≥1.4時，其比率達到1,覆蓋面積相同。故斷裂高分維值區域且分維值D≥1.4,一定是礦點分布的高分維區,且分形特征明顯,即礦點分布密集。從分形角度可理解為，分維值高的礦點分布區一定是受斷裂控制,但分維值低的礦點不一定完全是由斷裂控制。通過比對安徽省礦產資源分布圖的地理位置發現, 廬江、寧國一帶,懷寧以南, 定遠以南,蕪湖以北,淮南北部等地是礦點受斷裂構造影響強烈區。此外， 在斷裂構造最復雜處存在某一類型高分維礦點與之對應,即此處礦點受斷裂構造影響最強烈,對比礦產資源圖的地理位置為定遠以南的銅礦,表明該處銅礦受構造控制,符合該處銅礦床斷裂構造控礦模式。故通過分形分維結果,可知安徽省內總體礦點的分布不是主要受斷裂控制的,但當斷裂分維值D≥1.4時,對應安徽省礦點分布的高分維區,表明分維值高的礦點一定是受斷裂控制的。

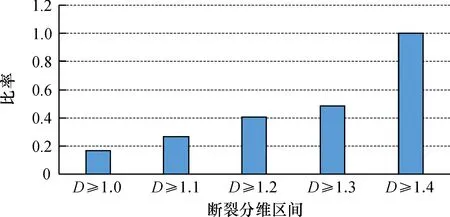
圖9 不同斷裂分維區間下礦點分布比例Fig.9 Distribution proportion of ore spots in different fault fractal dimension intervals

4 結 論

利用分形理論計算了安徽省礦點分布的分形值,從分形的角度建立了安徽省內主要形跡水系和斷裂與礦點分布的關系。

(1)安徽省礦點分布的分維值D=1.337 1,相關系數R2=0.981 7,礦點分布具有顯著的分形特征。

(2)安徽省總體水系的分維值D=1.582 5,主要水系淮河、長江和新安江的分維值依次是1.383、1.331和1.02,安徽省礦產資源分布點的分維值1.337 1與長江水系的分維值1.331最接近,表明安徽省的礦產資源分布受長江水系影響明顯,且分維值在1.3～1.4的水系有利于成礦。水系分維值可以反映水系所處流域地貌侵蝕發育程度,而地貌侵蝕發育程度又與風化型礦產資源相關聯;強烈的河流地質作用, 又使得大量的礦產資源外露,有色金屬礦產、非金屬礦產相對集中。

(3)安徽省斷裂分維值為1.568 4,與礦點分布的分維值1.337 1差異大,說明安徽省礦點分布受斷裂影響不大； 但當斷裂分維值D≥1.4時,對應安徽省礦點分布的高分維區,表明分維值高的礦點一定是受斷裂控制,且分形特征明顯。斷裂高分維值區與礦點分布的高分維區完全重疊,為礦點受斷裂構造影響最強烈區,表明該處為斷裂構造控礦模式。

(4)分形理論可以成為成礦預測、成礦模式研究和礦產資源規劃的重要的方法,尤其在研究看似雜亂無章的礦點分布規律上顯得非常有價值。