基于復雜軌跡的分段式機械臂軌跡規劃

林孟豪,張 蕾,李鵬飛,王曉華

(西安工程大學 電子信息學院,陜西 西安 710048)

0 引 言

隨著工業自動化以及計算機技術的不斷提高,機器人技術廣泛應用于各行各業,極大地提高了勞動效率,減少了人工負擔[1-3]。多關節機械臂作為機器人技術高度集成化和智能化的體現,能夠有效地節省機器人的工作空間,降低工業生產成本[4-6]。由于機械臂的控制精度很大程度上依賴于控制方法的設計[7],因此機械臂控制方法的研究極其重要,而機械臂的軌跡規劃問題是機械臂運動控制的第一要素[8]。軌跡規劃技術的設計方法影響著機械臂的運動形式和作業效率。隨著機械臂的應用越來越廣泛,機械臂的軌跡規劃研究逐漸成為國內外學者的研究熱點[9-10]。

鄒麗梅等通過DH建模的方法,建立了機器人正運動學模型并且求得其逆解,為實際應用提供了理論基礎[11]；劉子貴等對比了多項式插值算法中三次多項式與五次多項式的運行效果,證明五次多項式插值軌跡規劃的效果優于三次多項式插值[12]；李振娜等采用S型速度算法與弧長增量插補技術進行軌跡設計,驗證了該方法的運動性能較傳統的梯型速度算法有顯著地提高[13]。相比于國內學者的研究,國外學者ünsal等設計了一種多項式與B樣條曲線復合插值的改進復合多項式算法進行軌跡規劃。實驗結果表明,該算法所設計的曲線較為平滑,但增加了計算負擔,降低了效率[14]。Saravanan等通過對比NURBS曲線和B樣條曲線,采用NURBS曲線進行軌跡規劃。仿真結果表明,NURBS曲線能夠改善軌跡連接過渡的平滑性,更好地控制軌跡曲線的平滑度和曲率的連續性,但卻增加了使用難度,實際應用價值較低[15]。在工程應用中,以上方法為常用的軌跡規劃算法,通常將機械臂的運動軌跡設計為一條完整連續的路線,但是,上述方法均未考慮到機械臂運動軌跡的復雜性與不完整性,導致機械臂在作業時易出現運行精度較低,作業效率低下等問題。

本文通過機械臂正逆運動學分析,采用復雜軌跡分段式軌跡規劃設計方案,解決了機械臂運行軌跡復雜多變且不確定的問題。在抓取起始段，為了達到運行軌跡快速、便捷等設計目標,通過對比三次、五次與七次多項式插值算法的位移、速度、時間等設計參數,最終采用五次多項式插值算法設計此階段;在抓取過渡段，為了減少運行過程中震蕩、沖擊對機械臂整體性能的影響,通過對比梯型速度算法與S型速度算法的位移、時間、加速度等設計參數,最終采用S型速度算法設計此階段;在最終抓取段，為了達到準確、平穩等設計目標,采用NURBS曲線擬合算法設計此階段。仿真結果表明，分段式機械臂運行軌跡準確、光滑且無突變；進一步仿真實驗證明了該分段式軌跡規劃設計方案的正確性與靈活性。

1 復雜軌跡分段設計

選擇合適的軌跡規劃設計方案能夠有效地提高機械臂的工作效率。將機械臂的運動軌跡分為抓取起始段、抓取過渡段及最終抓取段3個階段,如圖1所示。其中抓取起始段是指:起始點(A)-靠近點(B)，抓取過渡段是指靠近點(B)-接觸點(C)，最終抓取段是指接觸點(C)-抓取點(D)。

抓取起始段如圖1(a)所示。抓取起始段中的起始點(A)為機器人在進行作業時,機械臂開始運動的位置,靠近點(B)為機械臂靠近目標物體的位置。為達到簡單、快捷并且方便確定軌跡邊界狀態等設計要求,此階段采用關節空間五次多項式插值軌跡規劃算法進行設計。

抓取過渡段如圖1(b)所示。過渡段中的接觸點(C)為機械臂受到目標遮擋物影響的位置。為達到緩解機械臂起停運動對整個系統造成沖擊和震蕩的設計要求,此階段采用笛卡爾空間S型速度算法進行設計。

最終抓取段如圖1(c)所示。抓取段中的抓取點(D)為機械臂抓取目標物體的位置。為達到抓取準確度高,平穩性強等設計目標,此階段采用笛卡爾空間NURBS曲線擬合軌跡規劃算法。

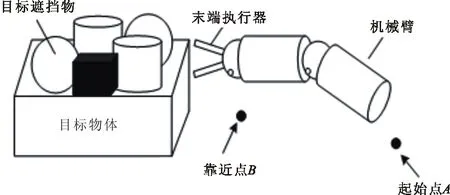
(a) 抓取起始段

2 分段軌跡規劃設計

2.1 抓取起始段

抓取起始段需要機械臂滿足運行快速、便捷且方便確定軌跡邊界狀態等目標,目前多采用三次多項式、五次多項式、七次多項式插值等算法進行軌跡規劃設計。此階段將對比三次、五次與七次多項式插值算法的規劃方法。

三次多項式中關節角度滿足[16]:

(1)

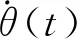
五次多項式中關節角度滿足[17]:

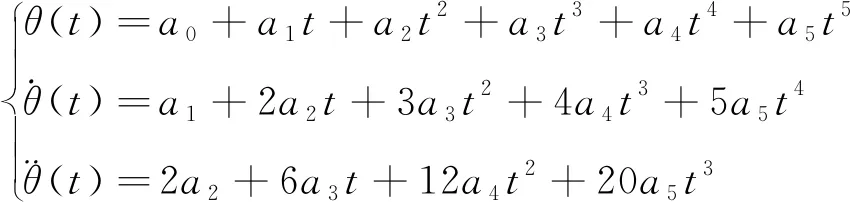
(2)

七次多項式中關節角度滿足:

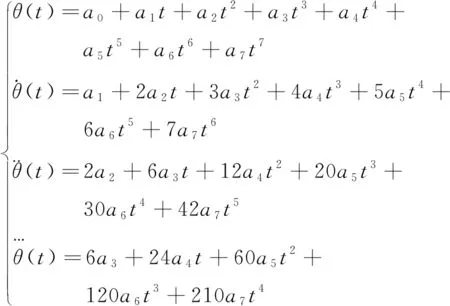
(3)

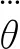
2.2 抓取過渡段

抓取過渡段需要達到降低震蕩與沖擊對整體性能影響的要求,目前多采用梯型速度算法與S型速度算法進行軌跡規劃設計。此階段將對比梯型與S型速度算法的規劃方法。

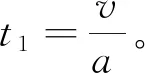
依據上述條件可得出梯型速度曲線的速度表達式為[18]

(4)

S型速度算法是在梯型速度算法的基礎上,增加了急動度的約束條件。其曲線可以分為加加速、勻加速、勻速、勻減速,減減速等5個階段。同理,S型速度曲線的速度表達式為[19]

v(t)=

(5)

2.3 最終抓取段算法

最終抓取段需要機械臂在作業時達到抓取準確度高,平穩性強等設計要求,目前多采用NURBS曲線擬合軌跡規劃算法進行設計。根據NURBS曲線的定義,NURBS樣條曲線可以表示為[20]

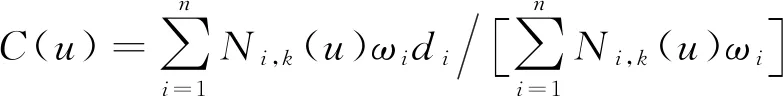
(6)

式中,Ni,k(u)為由節點矢量U定義的k次B樣條曲線基函數。最終，可以得到關節角位移、角速度、角加速度算式：

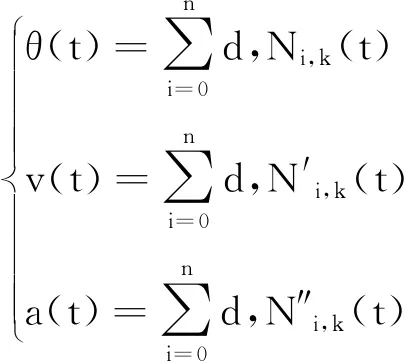
(7)

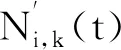
3 仿真分析

3.1 抓取起始段

為了驗證此設計方案對機械臂運行過程中平穩度、運行速度以及工作效率和經濟性的影響,在Matlab環境下對三次、五次與七次多項式插值算法進行仿真對比。參數設計如表1所示。表1中：θ0為起始關節角位移，θf為終止關節角位移，t0為起始時間，tf為終止時間，v0為起始速度，vf為終止速度，a0為起始加速度，af為終止加速度，j0為起始急動度，jf為終止急動度。

表 1 多項插值仿真參數

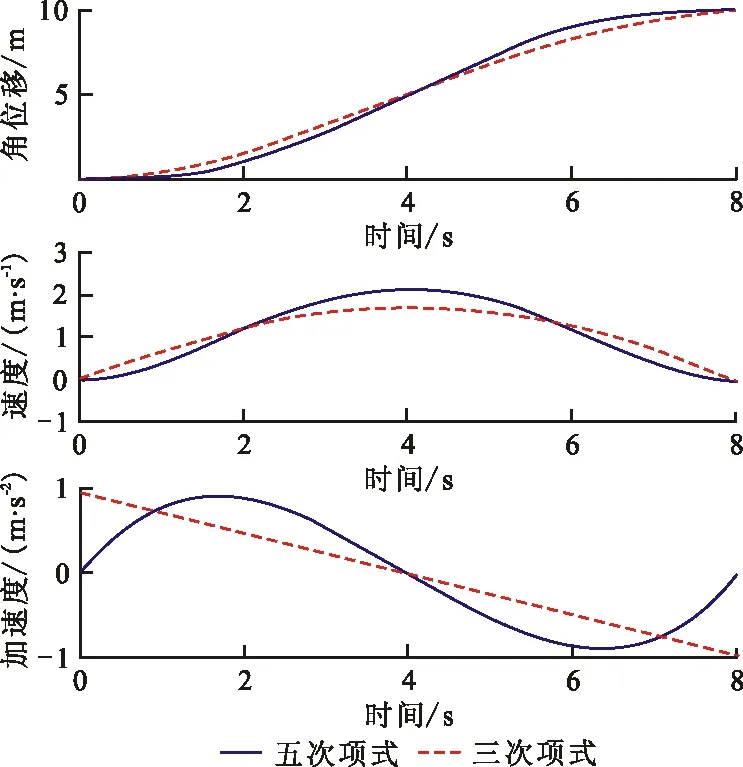
圖2為三次多項式與五次多項式軌跡對比圖。其中圖2(a)對應于表1中三次、五次多項式(Ⅰ)，圖2(b)對應于三次、五次多項式(Ⅱ)。如圖2所示:三次多項式插值算法能夠保證關節角位移以及角速度曲線的光滑連續,但是角加速度曲線呈線性變化,達不到加速度的邊界條件;五次多項式插值算法可以滿足關節角位移,角速度以及角加速度曲線光滑且連續。

(a) 三次多項式(Ⅰ)與五次多項式(Ⅰ)

圖3為五次多項式(Ⅰ)與七次多項式軌跡對比圖。如圖3所示,七次多項式插值算法較五次多項式插值算法增加了急動度的約束條件,其關節角位移、關節速度、關節加速度的平滑度有所提高,但增加了計算難度,降低了機械臂的運行效率,因而實際應用價值較低,成本較高。

(a) 五次多項式(Ⅰ)

比較三次、五次多項式插值算法，七次多項式插值算法計算復雜,效率低下。因此,在上述算法設計的基礎上,后續工作將側重于對三次、五次多項式插值算法的深入分析。今增設到5個抓取點進行研究，參數設置如表2所示。表2中：θ1、t1、v1分別為第一抓取點的關節角位移、時間與速度;θ2、t2、v2分別為第2抓取點的關節角位移,時間與速度;θ3、t3、v3分別為第3抓取點的關節角位移、時間與速度;θ4、t4、v4分別為第4抓取點的關節角位移、時間與速度;θ5、t5、v5分別為第5抓取點的關節角位移、時間與速度。

表 2 多點三次多項式插值與五次多項插值仿真參數

圖4為多點三次多項式與五次多項式軌跡對比。

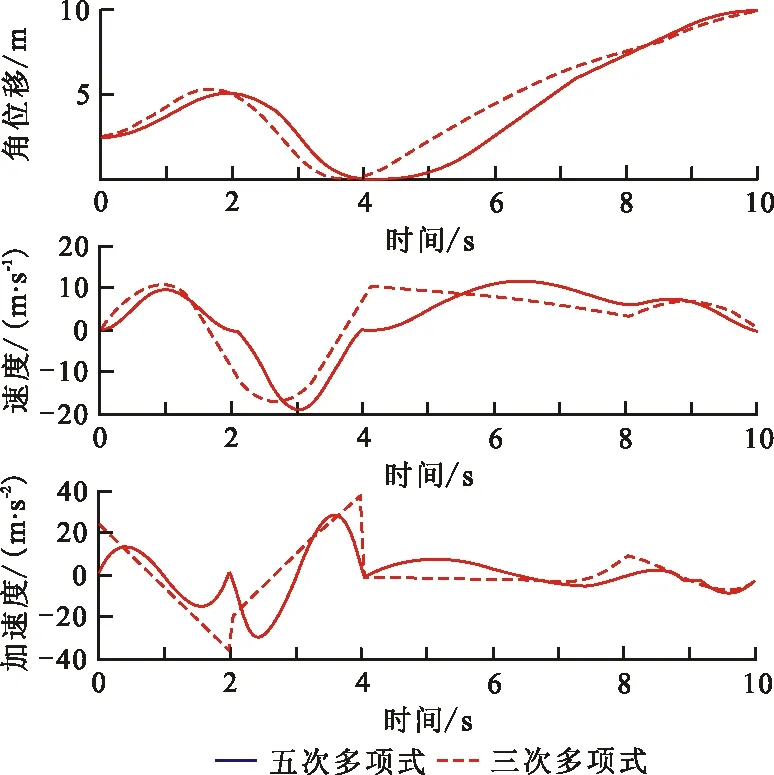
圖 4 多點三次多項式與五次多項式軌跡對比

如圖4所示,多點軌跡規劃更能直觀地看出此設計的優點：五次多項式較三次多項式插值算法中曲線的關節角位移、關節速度的平滑度有顯著提高。三次多項式不能夠保證各個點處的速度曲線平滑過渡,因此不能夠保證加速度連續光滑。五次多項式插值算法能夠解決機械臂關節加速度不連續的缺點,保證了機械臂在每個插值點工作時,能夠穩定安全地運行,減少運行沖擊對機械臂帶來的損害,并且此算法計算相對簡單。在此仿真實驗所設定的參數條件下,速度最大能夠提升14.2%。對比三次、五次與七次多項式插值算法,其中五次多項式插值算法更適用于本設計方案,故抓取起始段采取五次多項式插值算法進行軌跡規劃設計。

3.2 抓取過渡段

為了驗證設計方案的有效性,將梯型速度與S型速度算法進行對比分析。在Matlab環境下對梯型速度算法和S型速度算法行仿真對比。梯型速度算法參數與S型速度算法參數設計如表3所示,表3中amax為最大加速度。圖5為梯型速度軌跡圖，圖6為S型速度軌跡圖。

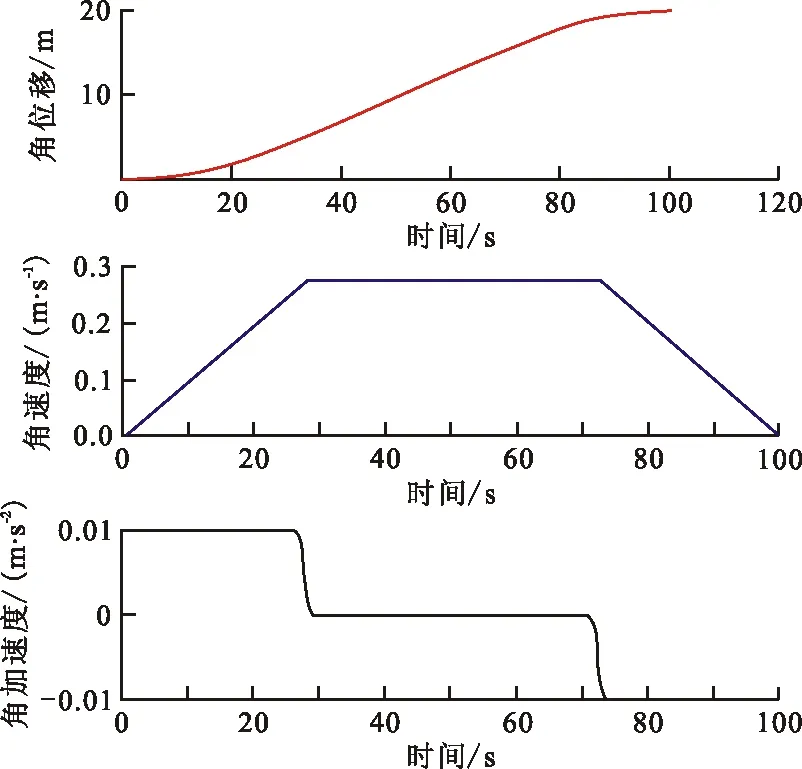
圖 5 梯型速度軌跡

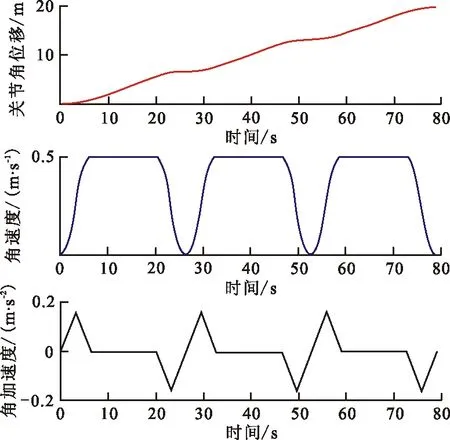
圖 6 S型速度軌跡

如圖5所示,梯型速度算法曲線過渡不夠平滑,加速度呈現階躍式突變,容易對機械臂的穩定性造成影響,引起震蕩。雖然梯型速度算法相比于其他算法易于實現、控制設計方案相對簡單,但是速度曲線不平滑,加速度也存在突變,會對機械臂的運行造成沖擊,僅適用于低成本、低精度的運動控制過程。

如圖6所示,S 型速度算法能夠保證機械臂在加減速過程中平滑過渡,減少加減速度變化對機械臂的控制系統造成沖擊。該算法解決了梯型速度算法中速度過渡不平滑,加速度容易產生突變等缺點,適用于高精度的運動系統。在此仿真實驗所設定的參數條件下,最大速度能夠提升5%。因此,抓取過渡段采用S型速度算法進行軌跡規劃設計。

3.3 最終抓取段

為了驗證本設計方案的準確性,最終抓取段采用NURBS曲線擬合算法進行軌跡規劃。在Matlab環境下對NURBS曲線擬合軌跡規劃算法進行驗證,結果如圖7所示。圖7中,黑圓點為通過NURBS反算推導出的控制頂點,虛線表示各控制頂點確定的控制曲線,實線表示通過NURBS擬合后的機械臂期望作業軌跡。

在2D平面內任取4個抓取點,分別為(100,200),(250,300),(400,100),(356,200),機械臂作業軌跡如圖7(a)所示。

(a) 2D NURBS擬合曲線

為了更好地展示此算法的優勢,在3D空間內任取4個抓取點,分別為(100,200,200),(250,300,600),(400,100,300),(356,200,148),機械臂作業軌跡如圖7(b)所示。

機械臂在復雜軌跡作業過程中,會有多個控制點；為驗證該算法的可行性，故設計多個抓取點。在3D空間內任取7個抓取點,分別為(100,200,200),(250,300,600),(400,100,300),(356,200,148),(400,250,153),(300,320,40),(250,260,-148),機械臂作業軌跡如圖7(c)所示。

NURBS曲線擬合過程中,通過調整各抓取點的權重值調整機械臂運行軌跡的走向；在實際作業過程中,可通過自適應調節各抓取點的權重值，以實現局部軌跡的調整。通過圖7可以看出,擬合后的作業軌跡光滑無突變,且為最優軌跡路線,適用于高精度、高穩定性、高準確度的軌跡規劃。此算法控制目標明確,能夠滿足此階段機械臂的工作要求,因此，最終抓取段采用NURBS曲線擬合算法設計。

4 結 語

采用分段式軌跡規劃設計方案,實現了機械臂在復雜多變軌跡中的軌跡規劃任務。針對設計方案所提出的抓取起始段、抓取過渡段及最終抓取段,分別采用五次多項式插值算法、S型速度算法、NURBS曲線擬合算法進行規劃設計。通過實驗仿真,證明了該設計方案具有便捷、可靠,通用性較強等特點,并且可以滿足機械臂在不同的復雜作業現場,快速、準確地完成抓取任務,為后期的研究奠定了理論基礎。本研究的后期工作是將該設計方案應用在機械臂的開發平臺上,采用C++語言編程,實現本設計方案。