基于交叉熵的粒子群優化算法

張 娜,賀興時,屈思凡

(西安工程大學 理學院,陜西 西安 710048)

0 引 言

粒子群優化算法(particle swarm optimization, PSO)是Eberhart和Kennedy在1995年基于對鳥群覓食行為的研究,提出的一種解決最優化問題的群體智能算法[1]。粒子群優化算法結構清晰,沒有過多約束條件,適合大規模計算。因此，該算法一經提出就倍受推崇且已經成功應用于諸多領域。隨著科學技術的發展,人們在路徑規劃[2]、圖像分割[3]、神經網絡[4-5]、數據預測[6]、噪聲控制[7]等領域面臨的優化問題愈發復雜。傳統的粒子群優化算法,容易陷入到局部極小點，存在“早熟收斂”現象,且對于高維復雜的多模態函數求解無法滿足實際的需求。

為提高算法性能,許多學者提出了不同的改進方法。目前對于算法的改進主要從3個方面進行：

1) 參數設置：如學習因子調整、慣性權重調節、公式調整等。郭巳秋等建立了新的慣性權重調節機制,根據進化中每個粒子的狀態調整慣性權重,提高了算法的收斂效率,增強了算法的魯棒性[8];趙乃剛在二階震蕩粒子群算法的基礎上,省略速度更新公式并將迭代公式降為一階,既保障了算法收斂精度又提升了搜索速度[9]。

2) 將混合策略引入到基本的粒子群優化算法：Mojarrad等為擴大種群多樣性，采用混沌映射初始化粒子群優化算法[10];劉召軍將自適應混沌列入差分進化算法，進而融合到粒子群優化算法中、搜索能力和算法的求解精度及效率[11]。

3) 將其他的智能優化算法與標準粒子群優化算法結合：為提高算法的全局尋優能力和收斂速度,Chen等在粒子群算法中引入魚群算法[12];Garg在粒子群優化算法中融入遺傳算法中的選擇機制,改進后的算法對高維復雜函數優化問題，尋優效果較為顯著[13]。

目前,不同的改進方法對于粒子群優化算法的整體性能在不同程度上均有所提高，但仍未能徹底解決粒子群優化算法對高維復雜函數尋優能力不佳,易陷入局部最優的問題。針對這一問題,本文從引入其他智能算法和混合策略入手,通過引入具有良好全局優化能力、自適應性以及魯棒性的交叉熵算法,以增強算法的尋優能力。隨后，采用粒子重構策略擴大種群的搜索范圍,避免早熟收斂。

1 粒子群優化算法

1.1 算法介紹

將鳥群中的每一只鳥抽象為一個“粒子”,位于n維搜索空間中的每個粒子都是潛在的最優解。其中第i個粒子的位置為Xi=(xi1,xi2,…,xin),速度為Vi=(vi1,vi2,…vin)。每個粒子的適應度值都可以用目標函數和粒子位置確定。PSO算法根據粒子自身或者同伴的歷史最優位置,通過更新公式迭代調整粒子位置以尋求最優解。Clerc等將壓縮因子引入速度更新公式,速度和位置更新公式[14]為

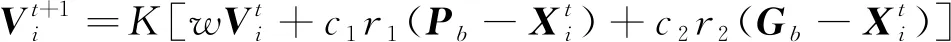
(1)

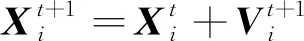
(2)

式(1)、(2)中：Pb和Gb分別表示當前個體最優位置和全局最優位置;w是慣性權重;r1,r2是區間[0,1]的隨機數,用于維持種群多樣性;c1,c2是學習因子,分別代表認知因子和社會因子;K表示壓縮因子,通常取0.729。

1.2 參數調整

慣性權重用于衡量粒子的上一迭代速度對當前速度的影響。選擇了Chatterjee等提出的慣性權重非線性遞減策略[15],并指出m=1.2時算法性能最優,其中w表示為

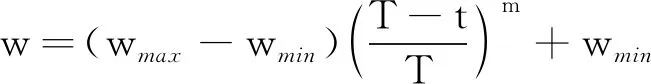
(3)

式中：wmin為最小值，通常取0.4；wmax為最大值，通常取0.9；T為最大迭代次數；t表示當前迭代次數；m是冪級數。

學習因子是體現粒子學習能力的參數,分別表示粒子向個體與全局歷史最優位置的學習能力。張健等提出一種結合慣性權重遞減與約束因子方法的PSO算法[16],在假設c1=c2的前提下，提出c1,c2取值隨慣性權重變化而變化的函數式。結合文獻[14]對因子取值的建議，即(c1+c2)/2=1.494 45,將學習因子調整為

(4)

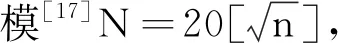
1.3 粒子重構

1.3.1 替換概率 粒子重構通過以一定概率替換進化能力較弱的粒子實現,替換概率是衡量進化能力弱的粒子是否被替換的標準。采用粒子適應度值的好壞度量替換概率,如式(5)所示:

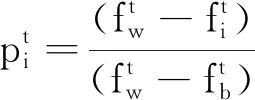
(5)

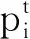
1.3.2 重構流程 在算法進化過程中,粒子的進化能力各不相同。選擇進化能力較好的粒子,根據式(6)對其添加高斯擾動生成新粒子：

(6)

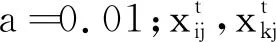
采用高斯擾動后的位置作為替換目標進行粒子重構,以避免迭代后期種群多樣性降低而導致早熟收斂。粒子重構的基本步驟如下:

1) 排序。計算每個粒子對應的適應度值并得到適應度值序列,將該序列中的元素從小到大排序得到新的矩陣序列。

2) 選擇。計算該序列的(1-q)分位數,分位數之前的p個粒子為進化能力強的粒子,末尾的p1(其中p1=N-p)個進化能力較弱的粒子為待替換的粒子。

3) 替換。在第t次迭代中,依次對進化能力較弱的p1個粒子進行替換。根據式(5)計算第i個粒子的替換概率,并根據式(6)對該粒子的各個維度進行替換,生成新的粒子。

4) 合并。將新生成的粒子與進化能力較強p個的粒子合并,構成新的粒子。

2 交叉熵算法

交叉熵(cross entropy,CE)方法[18-19]是1997年由 Rubinstein等提出的一種可靠性分析與隨機優化設計的統一方法,其本質是將最優化問題轉化為某一小概率事件估計問題。

設χ上的一個概率密度函數族為{h(..,v),v∈ν},將最小化問題轉化為研究f(x)比給定實數γ小的概率問題,即

l=Pu(f(x)≤γ)=Eu(I{f(x)≤γ})

(7)

設X是依據概率密度h(..;u)產生的隨機樣本,Eu表示相應的期望。通過構造參數序列{vt,t≥0}和級別序列{γt,t≥0},同時更新迭代vt,γt,基本步驟如下:

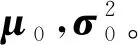
2) 設置參數。包括設置最大迭代次數T、隨機樣本個數N、分位數系數ρ0、平滑常數β,初始迭代次數t=0。

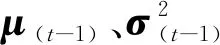
4) 排序。計算每個樣本對應的適應度值并得到適應度函數值序列；將該序列中的元素從小到大排序,得到新的矩陣序列；計算該序列的(1-ρ0)分位數γt。

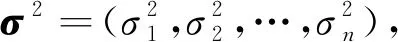
(8)

式中：L=1，2，…,n。

6) 平滑。

μL=βμL,t+(1-β)μL,t-1

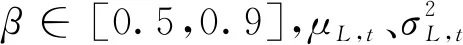
7) 停止。滿足到達最大迭代次數后停止迭代,否則返回重新執行1)～6)。

3 改進的粒子群優化算法

基于交叉熵的粒子群優化算法,基本執行過程為：在每次迭代中先用交叉熵算法產生全局最優的替代值,然后引入粒子重構策略,通過替換進化能力弱的粒子構造新的粒子。基本流程如圖1所示。

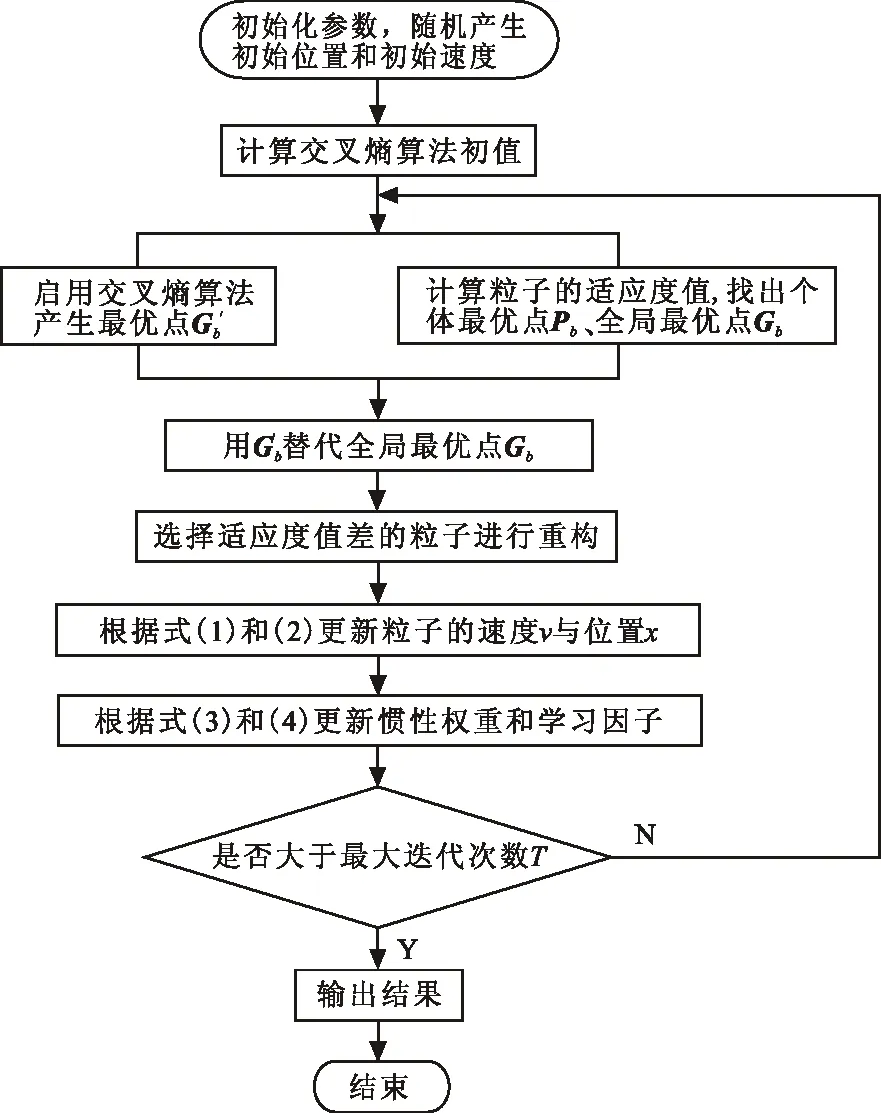
圖 1 CEPSO算法流程圖

1) 隨機產生初值,設置參數，初始化參數w,c1,c2，T,N,n等。

2) 計算初始種群每一個維度的均值、方差作為交叉熵算法的初始參數。

5) 選擇適應度值差的粒子進行重構。

6) 根據式(1)和(2)更新粒子的速度與位置。

7) 根據式(3)、(4)更新粒子i在第t+1代的慣性權重及學習因子。

8) 如果達到最大迭代次數,立即停止迭代并輸出最優解,否則返回3)。

4 仿真實驗

為了驗證CEPSO算法的性能,選取了8個標準測試函數[20],對本文算法(CEPSO)、粒子群優化算法(PSO)、基于模擬退火的粒子群優化算法(SAPSO)、改進的粒子群優化目標跟蹤算法(OTPSO)、采用粒子群優化的自適應樣條擬合算法(SPSO)等5種算法進行仿真對比。

4.1 參數設置

算法的參數均依據原始參數設置,5種算法的參數設置如表1所示。本次實驗對5個算法設置相同的種群規模和最大迭代次數,以確保實驗結果的有效性。在SPSO算法中c表示學習因子,w表示速度慣性,k表示除自身之外的鄰域個數。

表 1 參數設置

4.2 測試函數

選取了表2所示的8個不同標準測試函數。為驗證算法對復雜多模態函數的求解能力,選取了5個高維多峰函數F1～F5,用于測試算法跳出局部最優值的能力；3個高維單峰函數F6～F8，用于檢測算法收斂性能。

表 2 測試函數

4.3 結果分析

采用8種標準測試函數對5種算法的收斂速度和收斂精度進行測試。為避免算法的隨機性對分析結果造成影響,每種算法均獨立運行50次,結果如表3所示。表3中最優(差)解、平均值、標準差分別反應算法解的質量,整體水平以及魯棒性。

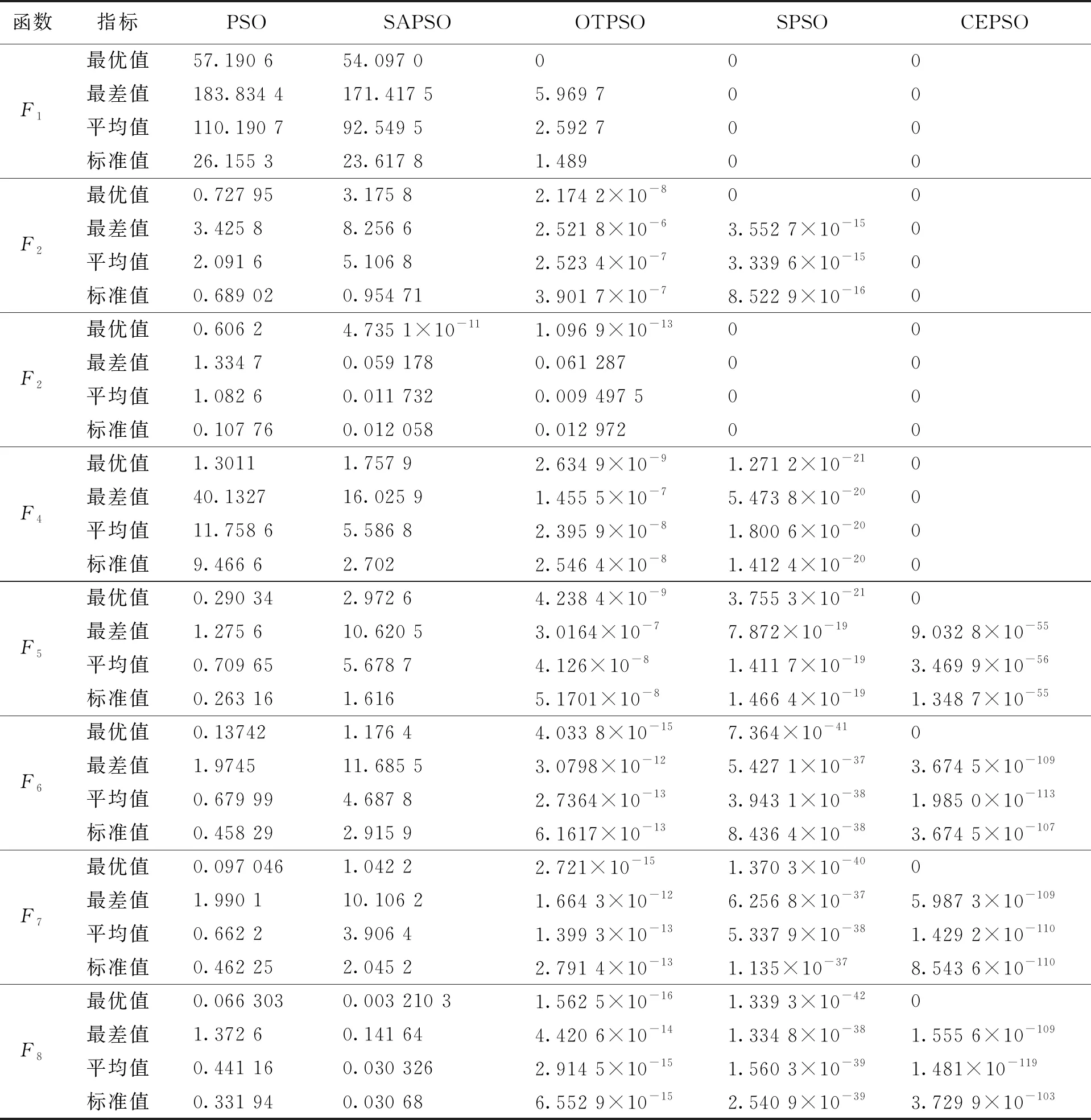
表 3 算法運行結果

從表3可以看出:對函數F1～F4,CEPSO算法均找到了真實最優值且魯棒性強;對函數F5～F8,CEPSO算法求解精度比其他幾個算法提高了幾十個數量級。對于高維多峰函數F1、F3,SPSO、CEPSO算法在收斂精度上有顯著優勢；但對于函數F2、F4、F5,SPSO算法收斂過早,而CEPSO算法始終保持著最高的收斂精度。說明改進后算法可以有效提高算法收斂精度,增強算法對高維復雜函數的求解能力。

圖2～9是5種算法針對不同測試函數的迭代曲線圖。

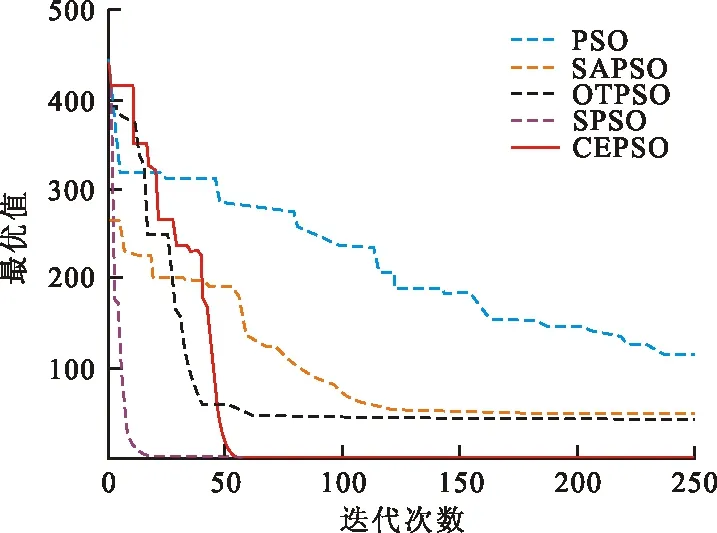
圖 2 F1迭代曲線

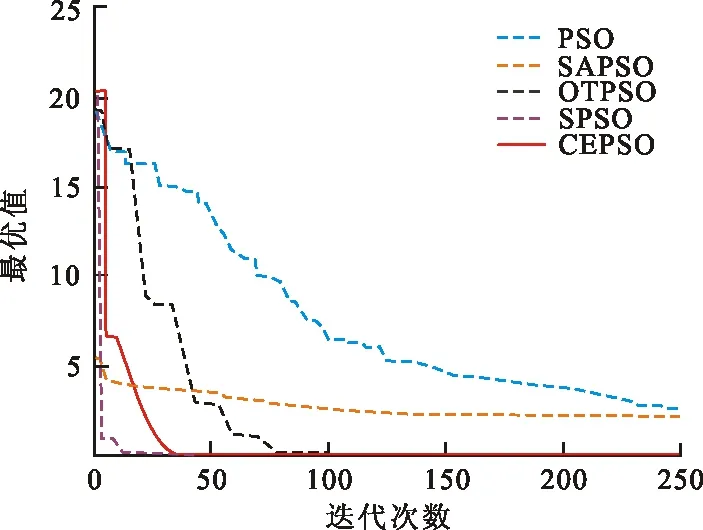
圖 3 F2迭代曲線

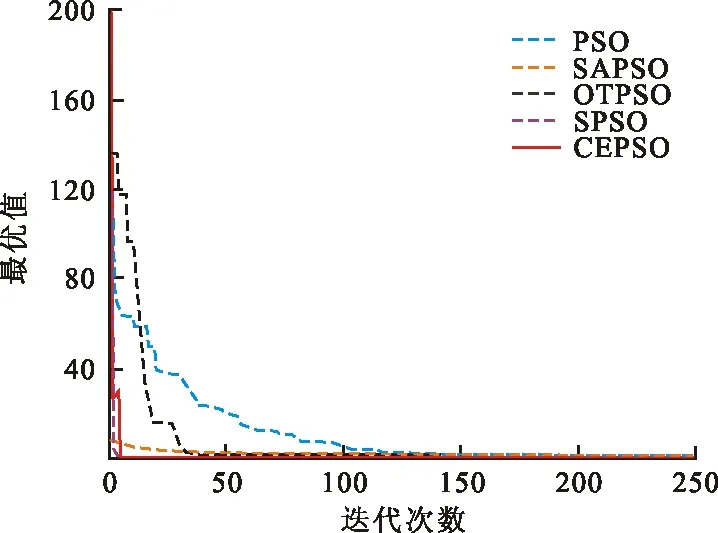
圖 4 F3迭代曲線

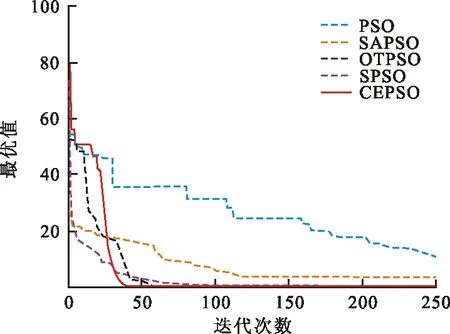
圖 5 F4迭代曲線

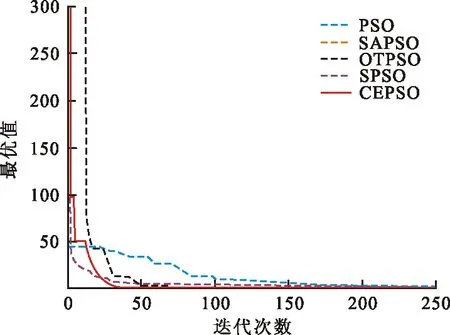
圖 6 F5迭代曲線

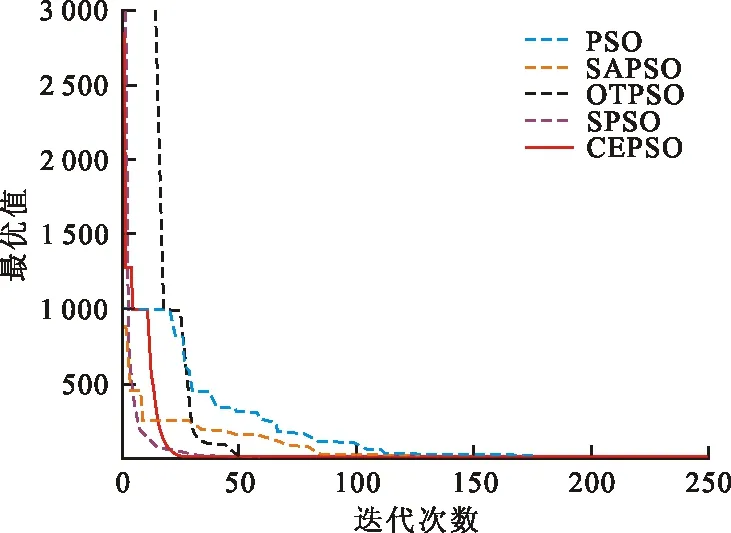
圖 7 F6迭代曲線 Fig.7 Iterative curves of F6

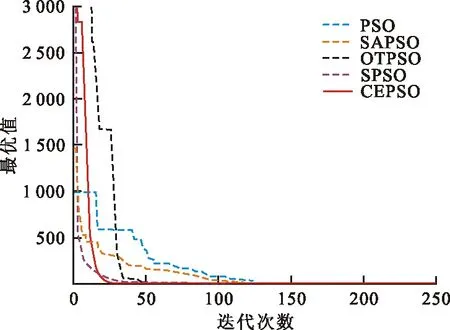
圖 8 F7迭代曲線

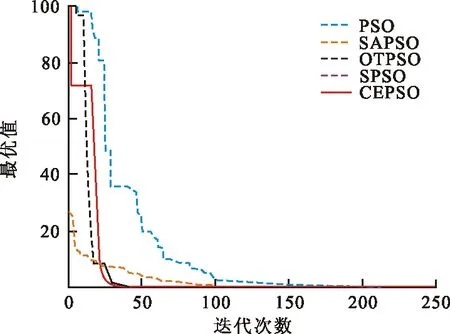
圖 9 F8迭代曲線

從圖2～4可以看出,對于高維多峰函數F1～F3,在進化初期CEPSO算法的個體質量不如其他算法。但是，隨著迭代次數不斷增加,PSO、SAPSO、OTPSO等算法都陷入局部最優值,而SPSO算法迅速找到了全局最優值,隨后CEPSO算法也收斂到全局最優值。特別是在圖4中，2種算法幾乎同時找到最優值。從圖5、6可以看出,對于高維多峰函數F4、F5,SPSO算法前期收斂速度快,但與其他算法一樣都陷入局部最優值,收斂精度不高,CEPSO算法在兼顧收斂速度的同時最先找到全局最優值。從圖7～9可以看出,對于高維單峰函數F6～F8,CEPSO算法最先收斂到最優值,在收斂速度和收斂精度上都有顯著優勢。由此可見，改進的算法在保障收斂速度的同時能收斂到全局最優值,在高維多峰函數的求解中更具優勢。

5 結 語

將交叉熵算法與粒子群優化算法結合,同時對進化過程中的粒子進行重構,拓寬了種群的搜索范圍,提高了CEPSO算法的收斂性能,使得算法能更高效地找到全局最優點。仿真實驗表明,改進后的算法在尋優精度和尋優速度方面均有明顯提升,對于復雜多模態函數效果尤為顯著。由此可見,將交叉熵算法引入粒子群優化算法，是一種有效的算法改進途徑。下一步將研究 CEPSO算法與其他優化算法的比較,并進一步研究其在多目標規劃問題中的應用。