跨學段任教話教學銜接

謝晶瑩

摘要：跨越小學與初中數(shù)學任教的一線教師，做好第二、第三學段教學銜接有得天獨厚的條件，也更有發(fā)言權，有利于學生數(shù)學素養(yǎng)的快速提升。本文結合跨學段任教的經(jīng)歷，從心理、知識、思維特征等方面，站在第二和第三學段視角，談談如何實現(xiàn)小學數(shù)學與初中數(shù)學教學的銜接。

關鍵詞：小學 ?初中 ?數(shù)學教學 ?銜接

中小學數(shù)學教學的銜接問題是一個熱門研究課題，已經(jīng)探索了很多年，也取得了較大的成效。然而由于小學老師只帶小學，中學老師只帶中學，平時交流也不多，在銜接上仍然存在斷層現(xiàn)象。筆者有幸任教于義務教育九年一貫制學校，有機會從小學一直跟班任教數(shù)學至初中，即跨越第二學段、第三學段，親歷小初銜接全過程。本文結合自己的切身歷練，談談對小初數(shù)學教學銜接的幾點思考。

一、跨學段心理的銜接，增強學習向往與可持續(xù)性

1.小學老師幫助學生克服畏難情緒，使之產(chǎn)生對中學數(shù)學的向往

筆者帶小學畢業(yè)班時，平時與學生交流較多，不少六年級學生打聽到中學數(shù)學和小學數(shù)學存在很大的差異，諸如中學數(shù)學內(nèi)容多、難度大、比較抽象……因而產(chǎn)生對中學數(shù)學的恐懼心理。都說興趣是最好的老師，有向往才有奔頭，因此在平時上課時，教師應適當對學生進行積極的心理暗示，讓學生產(chǎn)生對中學生活的向往。

例如，小學數(shù)學在計算圓的周長、面積及圓柱、圓錐的側面積、表面積和體積時，通常會用將圓周率π取3.14算出具體的結果，而在中學數(shù)學中基本上都是用圓周率π表示。因此，在題目沒有特別要求的情況下，我們就可以允許學生用圓周率“π”保留到計算的最后，讓學生體驗計算過程的簡便，滋生“巴不得馬上升入初中”的心理。又如，小學階段學習判定兩個相關聯(lián)的量是否反比例關系時，通常是計算出積是否相等，但我干脆引入反比例函數(shù)的圖像，告訴學生學了中學數(shù)學，就可以通過觀察圖像直接看出是不是反比例關系，讓學生體會中學數(shù)學方法的簡便性和優(yōu)越性，學生的“向往”之情油然而生。

2.中學老師幫助學生樹立數(shù)學好玩好學的心理體驗

學生從小學剛升入中學，本來就對中學數(shù)學有畏懼感，老師應予以理解，并時常關心、鼓勵、表揚。可以通過生動有趣的教學方法引導學生熱愛數(shù)學，使他們覺得中學數(shù)學也像小學數(shù)學一樣好玩，產(chǎn)生學好數(shù)學的心理體驗，從而樹立學好數(shù)學的信心，實現(xiàn)數(shù)學學習的可持續(xù)性。

例如，學習有理數(shù)乘法，根據(jù)負因數(shù)的個數(shù)判斷積的符號時，老師讓每個學生帶幾枚硬幣，進行翻幣實驗，正面朝上記為+1，背面朝上記為-1，然后根據(jù)負因數(shù)的個數(shù)確定積的正負。通過實驗，增強數(shù)學的趣味性，讓學生熟悉判斷方法，體會數(shù)學好玩。再如，學習相交線和平行線時，也像小學一樣，用課件播放生活中縱橫交錯的鐵軌、雙杠上的兩條木杠、黑板的上下邊緣等具體情境，借助學生熟悉的生活畫面，吸引學生的注意力，從中發(fā)現(xiàn)相交線和平行線，滲透從實物中抽象出簡單幾何圖形。這樣，就可以不斷積累良性的心理體驗。

二、跨學段知識的銜接，打造螺旋上升態(tài)勢

1.小學老師適當拔高要求，逼學生“跳一跳摘桃子”

小學數(shù)學通常是通過舉例、觀察、測量、實驗等方法得出結論，對結論并不作詳細的推理論證，導致很多學生認為通過這些方法得出結論就是證明，從而不利于中學數(shù)學中一些推理證明的學習。因此，在小學階段，尤其是小學高年級，教師可以對一些問題稍微延伸拔高要求，進行適當?shù)恼撟C，滲透一些中學數(shù)學的思想方法。

例如，組織學生探索三角形的三邊關系時，小學教材上是讓學生準備幾根長度不同的小棒，通過擺一擺，看哪些長度的小棒可以拼成三角形，然后得出結論“三角形的兩邊之和大于第三邊”。在六年級復習階段，再次探索三角形的三邊關系時，由于通過擺小棒得出的結論不夠嚴謹，我趁機引導學生把三角形的一條邊看成一條線段、另外兩條邊看成這條線段兩個端點之間的一條連線，根據(jù)“兩點之間的所有連線中，線段最短”，也可以得出比較嚴謹?shù)慕Y論，而這恰好是中學探索三角形三邊關系的方法。實踐證明，學生是完全可以理解的。又如在《確定位置》這一單元中，用數(shù)對表示點的位置時，小學課本是先寫行再寫列，經(jīng)常有學生記錯順序，因此我們可以因勢利導，順便簡單滲透一下中學的平面直角坐標系知識，水平的那條數(shù)軸表示X軸，垂直的那條數(shù)軸表示Y軸，在寫數(shù)數(shù)對時先X后Y，在教學中不妨嘗試了一下，效果很好，此后基本沒有同學再寫反了。

2.中學老師隨時彎下腰，“牽手”小學知識點

小學數(shù)學的一些知識點可以成為中學數(shù)學知識的生長點，《義務教育課程標準》就是按照九年一貫制的數(shù)學知識點整體設計、螺旋上升的。因此，中小學數(shù)學老師對于九年三學段的課程標準應做到心中有數(shù)，達到融會貫通。在探索解決中學數(shù)學問題時，先引導學生回顧小學階段解決類似問題的方法，在已有經(jīng)驗的基礎上進一步深入學習，謙恭彎腰，牽手小學知識點。

例如，中學老師在引導學生學習分式的乘除時，可以先復習小學學過的分數(shù)乘、除法，帶領學生根據(jù)分數(shù)乘、除法的法則，猜想b/a .d/c=？ b/a÷d/c=？然后用自己的語言總結出分式乘除法的法則，逐步引導學生從具體的“數(shù)”過渡到“式”。

三、跨學段思維的銜接，實現(xiàn)形象思維向邏輯思維飛躍

1.小學老師幫學生從具體形象思維過渡到抽象邏輯思維

由于小學數(shù)學逐漸從具體形象思維過渡到抽象邏輯思維，因此我們可以在第二學段著手，通過舉一反三、一題多解、變式訓練等方式，加大對學生思維訓練的力度，未雨綢繆，幫助學生順利實現(xiàn)小初銜接。

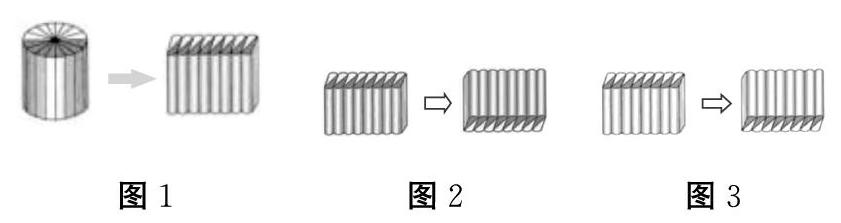
例如，在推導圓柱的體積公式時，我們通常是把圓柱等分成若干份，然后拼成一個近似的長方體（如下圖1），再根據(jù)長方體的體積公式得出圓柱的體積公式=底面積×高。為了加大對學生思維訓練的力度，同時也為了加深學生對這一推導方法的理解，我們可以把拼成的長方體換一種擺放方式（如下圖2），這時可以得出圓柱的體積=圓柱側面積的一半×底面半徑;如果再換一種擺放方式（如下圖3），則可以得出圓柱的體積=增加的表面積的一半×底面圓周長的一半。通過這三次操作，使學生明白萬變不離其宗，推導的依據(jù)都是根據(jù)長方體的體積公式=底面積×高，加深了學生對推導過程的理解和思考。

2.中學老師要讓學生從具體形象思維到邏輯思維成為現(xiàn)實

小學數(shù)學一般不需要通過邏輯推理，只需要看一看、量一量、畫一畫就可以得出正確答案。中學生抽象思維占主導成分，不能停留在小學形象思維層次原地踏步。

例如，中學在探索三角形的內(nèi)角和是180度時，是通過三角形的一個頂點作平行線，然后根據(jù)內(nèi)錯角相等或同位角相等，把三角形的三個角移到一起構成平角。嚴密的邏輯思維，無懈可擊。此時，不妨讓學生回顧一下自己小學時是把一個三角形的三個角撕下，通過剪拼移到一起，得到一個平角。小學思維的稚嫩彰顯出中學邏輯思維的巨大魅力。

小初銜接的重要陣地就是課堂。在九年一貫制教育模式下，小學和初中老師具備跨學段任教的可能性，給小初數(shù)學銜接創(chuàng)造了便利條件，有利于教育銜接一體化，不容易造成專業(yè)偏見。小學高年級和初中七年級是溝通小學和初中學習的橋梁，在這個關鍵節(jié)點，小學數(shù)學教師要提前接觸初中數(shù)學教學的特點，中學數(shù)學教師兼顧到小學數(shù)學的自然生長。另外，需要一批有責任、有擔當、有學識的專門隊伍，增強銜接階段教學本領，不斷消化吸收，教學相長。