基于自適應(yīng)代理模型的結(jié)構(gòu)動力可靠度分析方法

石巖，陳曉嵐，劉煒，李昕

(1.西北工業(yè)大學(xué) 航空學(xué)院， 西安 710072)(2.北京電子工程總體研究所 結(jié)構(gòu)與強度總體研究室， 北京 100854)

0 引 言

結(jié)構(gòu)動力可靠度分析能夠衡量結(jié)構(gòu)在動態(tài)載荷激勵下的安全狀態(tài)，對于評價結(jié)構(gòu)的工作性能具有重要的指導(dǎo)意義。對于在隨機過程激勵下的動力可靠度分析問題，傳統(tǒng)的分析方法往往僅考慮動態(tài)激勵載荷的隨機性而忽略了材料力學(xué)性能參數(shù)的隨機性。而對于實際的工程結(jié)構(gòu)，由于制造、工藝等的不確定性通常會導(dǎo)致材料力學(xué)性能參數(shù)也具有不確定性。因此，建立能夠同時考慮動態(tài)激勵載荷隨機性和材料力學(xué)性能參數(shù)隨機性的動力可靠度分析方法對于準(zhǔn)確度量結(jié)構(gòu)的安全程度具有重要的價值。

同時考慮動態(tài)激勵載荷隨機性和材料力學(xué)性能參數(shù)隨機性的動力可靠度分析已經(jīng)受到了越來越多研究者的重視，并且相關(guān)研究已經(jīng)取得了一定成果。陳穎等[1]仿照隨機變量響應(yīng)函數(shù)模式建立了結(jié)構(gòu)動力可靠度分析的響應(yīng)函數(shù)，并引用序列響應(yīng)面法來對響應(yīng)函數(shù)進(jìn)行擬合，從而將耗時的有限元模型調(diào)用轉(zhuǎn)化為確定的顯式功能函數(shù)的可靠性計算問題；陳建兵等[2]建立了一種不需要計算跨越率的概率密度演化方法來計算隨機振動的可靠度，所提方法同時具有較高精度且能夠在一定程度上減小計算成本；喬紅威等[3]通過分裂法[4]將多維動力可靠度響應(yīng)函數(shù)轉(zhuǎn)換為一維問題，并使用Hermite多項式來近似單隨機變量的動力可靠度響應(yīng)函數(shù)，最后結(jié)合數(shù)值模擬方法來對隨機激勵下的動力可靠度進(jìn)行求解；譚平等[5]提出使用Gauss-legendre積分公式來將隨機結(jié)構(gòu)地震激勵下的無條件動力可靠度的復(fù)雜積分問題轉(zhuǎn)化為積分點加權(quán)求和的形式進(jìn)行求解，提高了計算效率；楊英杰[6]利用概率密度演化理論進(jìn)行隨機激勵下非線性框架結(jié)構(gòu)的動力響應(yīng)以及可靠度分析，并考察了計算過程中有限差分步長和響應(yīng)量區(qū)間長度對可靠度分析的影響。以上這些方法在計算最終的動力可靠度時均使用了基于數(shù)值積分或點估計的計算過程，而這個過程不可避免地會引入計算誤差。

基于自適應(yīng)Kriging代理模型[7]的可靠性分析方法近年來受到了越來越多的關(guān)注。相比于通過給定樣本直接構(gòu)建代理模型而言，自適應(yīng)的代理模型能夠根據(jù)需要自主地篩選出對設(shè)定目標(biāo)貢獻(xiàn)最大的樣本點，從而能夠使用盡可能少的樣本點來獲得較好的代理結(jié)果。B.Echard等[8]根據(jù)Kriging代理的預(yù)測均值和方差，構(gòu)建出U學(xué)習(xí)函數(shù)來對結(jié)構(gòu)功能函數(shù)的極限狀態(tài)面進(jìn)行高效預(yù)測；B.J.Bichon等[9]通過構(gòu)建期望可行性函數(shù)(EFF)來對結(jié)構(gòu)功能函數(shù)進(jìn)行代理，所構(gòu)建的EFF同時考慮了樣本點與極限狀態(tài)面之間的距離以及預(yù)測樣本的變異性；Sun Z L等[10]提出最小提高函數(shù)(LIF)來衡量新訓(xùn)練樣本點的加入對失效概率的貢獻(xiàn)大小。若使用Kriging代理模型方法來對動力可靠度進(jìn)行計算，其構(gòu)建的為材料力學(xué)性能參數(shù)與條件動力可靠度之間的代理模型，而最終的動力可靠度為條件動力可靠度的均值。以上學(xué)習(xí)函數(shù)的本質(zhì)在于將功能函數(shù)的極限狀態(tài)面代理準(zhǔn)確，而非代理模型輸出的均值。因此，以上學(xué)習(xí)函數(shù)均不能直接用來構(gòu)建自適應(yīng)的Kriging模型對動力可靠度進(jìn)行計算。

陶瓷基復(fù)合材料具有輕質(zhì)性、高強韌性、抗氧化等優(yōu)異特性，因此將該材料應(yīng)用于航空發(fā)動機、飛行器機翼等結(jié)構(gòu)上能夠極大地減輕結(jié)構(gòu)的重量，提高其性能。近年以來，基于陶瓷基復(fù)合材料的結(jié)構(gòu)設(shè)計制造已經(jīng)成為研究重點[11-14]。

本文研究C/SiC陶瓷基復(fù)合材料蒙皮骨架結(jié)構(gòu)在承受隨機振動載荷環(huán)境下的動力可靠度分析問題。結(jié)合基于馬爾科夫過程假設(shè)[15-16]的動力可靠度計算公式，構(gòu)建材料力學(xué)性能參數(shù)與條件動力可靠度之間的Kriging代理模型；基于Kriging模型推導(dǎo)計算動力可靠度的解析表達(dá)式；提出一個新的學(xué)習(xí)函數(shù)構(gòu)建自適應(yīng)的Kriging代理模型，并進(jìn)行可靠度分析計算。

1 結(jié)構(gòu)動力可靠度分析

一般情況下，可將結(jié)構(gòu)在動態(tài)載荷作用下的動力響應(yīng)表達(dá)為y(t)。結(jié)構(gòu)的動力可靠度RT定義為動力響應(yīng)y(t)絕對值在時間區(qū)間[0,T]內(nèi)不超過安全界限值ε的概率，即

RT=P{|y(t)|≤ε,?t∈[0,T]}

(1)

在通過首次超越理論計算結(jié)構(gòu)的動力可靠度RT時，基于假定動力響應(yīng)y(t)與安全界限的交叉次數(shù)服從馬爾科夫過程可得到動力可靠度計算公式：

(2)

(3)

式中：Syy(ω)為動力響應(yīng)y(t)的自功率譜密度函數(shù)。

本文針對在隨機振動載荷和隨機材料力學(xué)性能參數(shù)作用下的C/SiC陶瓷基復(fù)合材料蒙皮骨架結(jié)構(gòu)的動力可靠度進(jìn)行求解，其中隨機振動載荷以PSD的形式進(jìn)行加載。在通過有限元軟件進(jìn)行模型的不確定性分析時，可直接輸出動力響應(yīng)y(t)的自功率譜密度函數(shù)Syy(ω)。

2 考慮材料力學(xué)性能參數(shù)不確定性動力可靠度高效算法

直接使用上一節(jié)中給出的公式計算結(jié)構(gòu)的動力可靠度時無法考慮材料力學(xué)性能參數(shù)的不確定性。在此使用X=[X1,X2,…,Xn]和x=[x1,x2,…,xn]分別表示需要考慮的具有隨機不確定性的n維材料力學(xué)性能參數(shù)向量及其實現(xiàn)值，則上一節(jié)中給出的計算公式僅僅能計算出在給定材料力學(xué)性能參數(shù)實現(xiàn)值x下的動力可靠度結(jié)果，記其結(jié)果為RT(x)。則同時考慮載荷隨機性和材料力學(xué)性能參數(shù)隨機性的動力可靠度RTX可計算為

(4)

式中:fX(x)為材料力學(xué)性能參數(shù)向量X的聯(lián)合概率密度函數(shù)。

式(4)為n維積分問題，由于在材料力學(xué)性能參數(shù)實現(xiàn)值x與動力可靠度RT(x)之間往往不具有顯式關(guān)系，因此解析求解公式(4)顯得尤為困難。求解上式的傳統(tǒng)方法為Monte Carlo(MC)模擬法，該方法通過抽取材料力學(xué)性能參數(shù)向量X的大量樣本，并計算在每一樣本下的條件動力可靠度結(jié)果，最終通過求解所有條件動力可靠度結(jié)果的均值來獲得RTX的結(jié)果。在抽取的材料力學(xué)性能參數(shù)樣本足夠大的情況下，該方法能夠獲得精確的動力可靠度RTX的結(jié)果。但是該方法需要大量的調(diào)用有限元分析軟件，因此其計算效率較低，在工程上往往不可行。為了提高計算效率，可通過各種點估計方法如稀疏網(wǎng)格法[17]產(chǎn)生少量樣本點來計算動力可靠度RTX。由于稀疏網(wǎng)格法是一種能夠同時兼顧計算精度和效率的高效點估計方法，本文以稀疏網(wǎng)格法計算得到的動力可靠度結(jié)果作為對照解。

2.1 基于Kriging模型的動力可靠度解析表達(dá)

(5)

cov(x(i),x(j))=σ2Rθ(x(i),x(j))

(6)

式中：x(i)和x(j)為不確定材料力學(xué)性能參數(shù)向量X的任意兩個實現(xiàn)值；σ2和Rθ(x(i),x(j))分別為穩(wěn)態(tài)高斯過程z(X)的方差和相關(guān)函數(shù)。

本文使用如下的相關(guān)函數(shù)：

(7)

式中：θk(k=1,2,…,n)為參數(shù)。

(8)

(9)

式中：F為回歸矩陣，其元素為Fij=hj(x*(i))(i=1,2,…,m;j=1,2,…,n)；R為相關(guān)矩陣，其元素為Rij=Rθ(x*(i),x*(j))(i,j=1,2,…,m)。

(10)

σ2[1-rT(x)R-1r(x)+uT(x)(FTR-1F)-1u(x)]

(11)

式中：r(x)=[Rθ(x,x*(1)),Rθ(x,x*(2)),…,Rθ(x,x*(m))]T且u(x)=FTR-1r(x)-h(x)。

一般情況下，在獲得條件動力可靠度RT(X)代理模型后，需要將其結(jié)合式(4)使用數(shù)值積分等方法來計算最終的動力可靠度RTX。雖然此時已不需要調(diào)用真實有限元分析軟件進(jìn)行計算，但是由于使用數(shù)值積分，這個過程往往會引入新的計算誤差。為了避免由于使用數(shù)值積分所導(dǎo)致的計算誤差，本文基于Kriging模型，推導(dǎo)出計算動力可靠度RTX的解析表達(dá)式。將條件動力可靠度RT(X)的Kriging預(yù)測均值代入式(4)，得到動力可靠度RTX的計算式：

RTX

(12)

(13)

在此使用0階回歸多項式，其對應(yīng)的回歸模型h(X)=1，此時回歸參數(shù)為β。并將r(x)的表達(dá)代入上式，將RTX表達(dá)為

(14)

式中：Rθ(x,x*(i))(i=1,2,…,m)由式(7)進(jìn)行求解。

(15)

式中：

(16)

式中：

(17)

(18)

式(18)中所有輸入量均為在構(gòu)建代理模型時可以得到，因此動力可靠度RTX可以通過上式便捷地進(jìn)行求解。同時，通過該解析表達(dá)式對動力可靠度RTX進(jìn)行求解可以避免使用數(shù)值積分時引入的計算誤差。

2.2 新學(xué)習(xí)函數(shù)

(4) 挑選出的新訓(xùn)練樣本點與已有訓(xùn)練樣本點之間不應(yīng)過于聚集，否則易導(dǎo)致代理模型在局部具有較高的預(yù)測精度而在全局預(yù)測精度較差，這對于RTX的計算精度有較大影響。

(19)

(20)

同時可求得V(x)的均值μV(x)為[20]

(21)

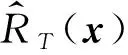
(22)

Lmin(x(i))=min {Li1,Li2,…,Lim}

(23)

使用Lmin(x(i))避免訓(xùn)練樣本點之間過于聚集的問題。

基于以上分析，可構(gòu)建針對樣本池中第i個樣本x(i)的學(xué)習(xí)函數(shù)表達(dá)式：

(24)

則能夠使學(xué)習(xí)函數(shù)M(x(i))最大化的樣本池中樣本點x(i)(i=1,2,…,N)需要被篩選出來更新Kriging代理模型，即新的訓(xùn)練樣本點x*(new)通過式(25)挑選：

(25)

由于動力可靠度RTX事先不知道，因此本文在計算μV(x(i))時均使用當(dāng)前的Kriging代理結(jié)合推導(dǎo)出的動力可靠度RTX計算公式(18)進(jìn)行求解。

2.3 自適應(yīng)代理過程求解動力可靠度

將自適應(yīng)Kriging代理模型方法結(jié)合所提出的新學(xué)習(xí)函數(shù)來計算動力可靠度RTX的計算步驟總結(jié)如下：

步驟1：使用材料力學(xué)性能參數(shù)向量X的聯(lián)合概率密度函數(shù)fX(x)產(chǎn)生N組樣本x=(x(1),x(2),…,x(N))作為樣本池，并隨機抽選出m組樣本作為初始訓(xùn)練樣本集x*=(x*(1),x*(2),…,x*(m))，結(jié)合式(2)計算相應(yīng)的條件動力可靠度結(jié)果。

步驟2：使用當(dāng)前的訓(xùn)練樣本集x*=(x*(1),x*(2),…,x*(m))和相應(yīng)的條件動力可靠度結(jié)果構(gòu)建Kriging代理模型。

步驟3：使用當(dāng)前的Kriging代理模型對樣本池中的樣本x=(x(1),x(2),…,x(N))進(jìn)行預(yù)測，并使用解析公式(18)計算動力可靠度RTX的結(jié)果。如果連續(xù)兩次計算得到的動力可靠度RTX相對誤差小于10-4，輸出當(dāng)前的RTX作為動力可靠度結(jié)果。否則，使用式(24)計算樣本池中樣本x=(x(1),x(2),…,x(N))對應(yīng)的學(xué)習(xí)函數(shù)的結(jié)果M(x(i))(i=1,2,…,N)。

步驟4：使用式(25)計算新的訓(xùn)練樣本點x*(new)并將其添加入訓(xùn)練集，結(jié)合式(2)計算在該樣本下的條件動力可靠度結(jié)果，令m=m+1并返回步驟2。

3 蒙皮骨架結(jié)構(gòu)動力可靠度計算

飛機蒙皮骨架結(jié)構(gòu)為飛機機翼典型構(gòu)型件，研究飛機蒙皮骨架結(jié)構(gòu)在隨機振動載荷下的動力可靠度分析問題對于評估飛機機翼的整體安全性能具有一定指導(dǎo)意義。在此通過本文提出的高效方法對飛機蒙皮骨架結(jié)構(gòu)在隨機振動載荷以及隨機材料力學(xué)性能參數(shù)共同作用下的動力可靠度進(jìn)行計算分析。簡化的蒙皮骨架結(jié)構(gòu)的尺寸如圖1所示。

圖1 飛機蒙皮骨架結(jié)構(gòu)尺寸

蒙皮骨架結(jié)構(gòu)承受的隨機振動載荷以加速度功率譜密度的形式進(jìn)行加載如圖2所示，持續(xù)時間為3 min。

圖2 隨機振動功率譜密度

具有隨機不確定性的材料力學(xué)性能參數(shù)包括C/SiC復(fù)合材料彈性模量E1和E2(其中1和2分別表示復(fù)合材料的兩個方向)，泊松比υ，面內(nèi)剪切模量G12、G13和G23，密度ρ以及結(jié)構(gòu)的阻尼比γ。由于復(fù)合材料屬性導(dǎo)致E1=E2，G13=G23。本文假定各個材料力學(xué)性能參數(shù)的分布類型及分布參數(shù)如表1所示，其中γ的變異系數(shù)為0.03，其余參數(shù)的變異系數(shù)為0.05。

表1 輸入材料力學(xué)性能參數(shù)分布類型及分布參數(shù)

使用Abaqus 15.0對圖1所示的飛機蒙皮骨架結(jié)構(gòu)進(jìn)行建模，以蒙皮中點(圖1所示A點)在垂直于蒙皮方向(沿z軸)的位移超過指定值ε定義為結(jié)構(gòu)失效。C/SiC復(fù)合材料的鋪層結(jié)果如圖3所示，復(fù)合材料按照0°和90°方向交替鋪設(shè)，單層厚度0.2 mm，夾持區(qū)鋪設(shè)30層，其他部分鋪設(shè)10層。

(a) 夾持區(qū)

(b) 蒙皮

(c) 橫筋

(d) 縱筋

蒙皮骨架結(jié)構(gòu)前四階模態(tài)如圖4所示，其中U3表示沿z軸的位移。

(a) 1階模態(tài)

(b) 2階模態(tài)

(c) 3階模態(tài)

(d) 4階模態(tài)

從圖4可以看出：蒙皮骨架結(jié)構(gòu)的前四階模態(tài)對應(yīng)的頻率分別為440.10，744.24，918.13和1 026.8 Hz。

在材料力學(xué)性能參數(shù)均值處A點沿z軸位移的功率譜密度曲線如圖5所示，可以看出：在如圖2所示的功率譜密度振動載荷作用下，對該蒙皮骨架結(jié)構(gòu)影響較大的為其前四階模態(tài)所確定的頻率范圍；且在1階模態(tài)對應(yīng)的頻率處，該蒙皮骨架結(jié)構(gòu)的響應(yīng)功率譜密度具有最大值，說明1階模態(tài)對振動載荷的響應(yīng)起主要作用。

圖5 在材料力學(xué)性能參數(shù)均值處A點沿z軸位移PSD曲線

不同閾值下的動力可靠度計算結(jié)果如表2所示，其中SP為稀疏網(wǎng)格方法；MC為Monte Carlo模擬方法；Kriging為本文提方法；Ncall為調(diào)用有限元模型進(jìn)行分析的次數(shù)。

表2 動力可靠度計算結(jié)果

從表2可以看出：所提自適應(yīng)Kriging代理方法具有較高的計算精度，同時能夠極大的減少計算成本；所提的自適應(yīng)Kriging代理模型方法的計算效率高于基于稀疏網(wǎng)格技術(shù)的方法，且隨著給定閾值ε的提高，自適應(yīng)Kriging代理模型方法的計算量減小，而基于稀疏網(wǎng)格技術(shù)的方法計算量保持為恒定值。

在ε=0.23時，提出的自適應(yīng)Kriging代理方法與非自適應(yīng)Kriging代理方法計算出的動力可靠度的收斂圖如圖6所示。

圖6 動力可靠度計算結(jié)果隨計算量變化圖

從圖6可以看出：通過結(jié)合本文所提新的學(xué)習(xí)函數(shù)來構(gòu)建自適應(yīng)的Kriging代理模型，可以極大地減小計算成本，提高收斂速度，同時結(jié)果具有較大精度。

4 結(jié) 論

(1) 本文采用了一種能夠同時考慮載荷隨機性和材料力學(xué)性能參數(shù)隨機性的動力可靠度計算新方法，通過構(gòu)建的Kriging代理模型推導(dǎo)出了動力可靠度的解析表達(dá)式，避免了由于基于Kriging模型使用數(shù)值積分方法對動力可靠度進(jìn)行求解時所引入的計算誤差。

(2) 提出了一種新的學(xué)習(xí)函數(shù)來篩選對計算動力可靠度有較大貢獻(xiàn)的新訓(xùn)練樣本點，所提學(xué)習(xí)函數(shù)同時考慮了預(yù)測值與動力可靠度的差異，預(yù)測值的標(biāo)準(zhǔn)差、預(yù)測樣本的密度和其與已有訓(xùn)練樣本點之間的距離。基于所提學(xué)習(xí)函數(shù)，可以構(gòu)建自適應(yīng)的Kriging代理模型過程，從而能夠使用盡可能少的計算成本獲得準(zhǔn)確的動力可靠度計算結(jié)果。

(3) 通過飛機蒙皮骨架結(jié)構(gòu)在振動載荷作用下的動力可靠度分析結(jié)果可以看出，所提高效方法不僅具有較高的計算精度，同時能夠極大地減少計算量，節(jié)約計算成本。