基于服役數據的飛機計劃維修任務間隔優化方法

林聰，蔣慶喜，周揚

(中國航空綜合技術研究所 裝備服務產品部， 北京 100028)

0 引 言

計劃維修要求(SMR)是保障一型裝備在服役階段持續可用的規范性文件，在民用航空領域指的是一型飛機的維修大綱(MRBR)，其主要內容通常包括維修間隔、維修對象、維修任務，即闡明“什么時間對什么設備執行什么檢修活動”。MRBR是EASA、FAA、CAAC、TCCA等適航當局強制要求飛機型號合格證持有者在研制過程中必須編制的文件[1]。在制定MRBR的過程中，對于計劃維修任務間隔(含門檻值和重復間隔)的選擇，由于缺少必要的數據，通常采取保守策略保證飛機安全性。飛機服役后，隨著使用和維修數據的積累，有必要對MRBR中任務間隔的有效性進行重新評估[2]。例如，空客于2005年發布的《A320飛機維修大綱》中對“A檢”間隔由500 fh(飛行小時)調整為600 fh，“C檢”間隔由15個日歷月調整為6 000 fh。

近年來，基于故障趨勢分析的可靠性預測及維修任務間隔優化得到了廣泛研究。例如，Hong Sheng等[3-4]基于性能退化數據對軸承的健康趨勢進行預測；S.Porotsky等[5]提出了基于PHM思想利用剩余壽命(RUL)來判斷是否需要對各個部件進行預防性維修。此類研究方法適用于軸承等細粒度部件的壽命趨勢分析，這類對象的工作條件相對單一，并且能夠產生充足的數據量來支撐建模分析。但是，這類方法給出的對維修間隔調整的建議是針對維修方案的，而不是針對維修大綱中的維修任務進行間隔調整。

對于維修大綱中任務間隔確定最樸素的想法是借鑒相似機型的歷史經驗，因此，Bai Wenhua等[6]開展了基于案例推理(CBR)的維修大綱制定方法。由于機型之間存在差異，使得制定新機型維修大綱時都采取偏向保守的原則，因此這種方法給出的維修任務間隔與飛機實際表現差距較大。

在實際運營過程中為了降低飛機的維護成本，航空公司會在MRBR規定的維修間隔內基于費用和風險評估思想調整維修任務的時機[7]。例如，A.Ahmadi等[8]對“非安全影響”和“安全影響”類別的隱藏故障，采用風險約束優化的方法，得出單位飛行小時成本最小的維修間隔；李景奎等[9]提出運用改進的三參數威布爾極大似然估計法，對歷史故障數據進行可靠性分析，并建立了可靠壽命區間約束下的部件最優定時維修費用率模型；以國航波音737NG機隊空調系統空氣循環機為例，張連磊[10]建立維修成本與預防性維修間隔的數學模型，尋找維修成本最小的預防性維修間隔；賈寶惠等[11]提出一種基于風險約束函數的平均不可靠度和成本率函數優化檢查和恢復間隔的模型。以上研究都是針對某一類具體對象開展的維修間隔優化研究，沒有給出通用的方法指導MRBR中任務間隔的優化。

由于對MRBR中計劃維修任務間隔進行調整的目標是希望改變維修間隔后不會增加飛機發生故障的可能性，通過擬合分析飛機故障與飛行小時的關系，判斷調整維修間隔可能對飛機的故障發生頻率造成何種影響。

本文給出針對某一項維修任務進行間隔優化的方法，包括確定相關數據的抽樣樣本量，通過擬合分析故障發生趨勢預判是否有必要對該任務進行間隔優化，基于故障到達的概率模型對新的維修間隔進行假設檢驗，并對該方法進行算例驗證。

1 確定維修任務及飛機樣本量

首先，在開展優化前需要確定當前已收集的維修數據量是否能夠支撐優化工作的進行。一型飛機的維修間隔優化工作需要收集該型飛機5年以上的故障、維修及運營數據，數據維度包括機隊規模、年平均利用率、數據收集時間、維修間隔、機齡等。

針對某一特定維修任務，基于上述數據可估算求得對該型飛機在數據收集期間所產生該任務的總數S為

(1)

式中：Na為機隊規模，架；Uy為每架飛機的年平均利用率，fh/年；Ts為數據收集時間，年；I為該維修任務的初始間隔，fh。

其次，需要確定從總體S中抽取多少條維修數據作為樣本，記為m。由于計劃維修任務的目的是通過定期對飛機進行檢查從而發現隱蔽性故障，因此，假設每次維修任務能夠識別并發現重要故障的概率為p以及可接受誤差范圍c。這兩個參數的取值可由型號設計及維修專家給定[12]，并得到維修審查委員會(MRB)的認可。

基于上述假設，定義每次檢查能夠發現故障的數量為Xi，該隨機變量服從0～1概率分布，即：

(2)

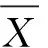
當置信度為1-α時，由標準正態分布的性質得到：

(3)

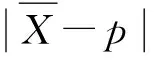
綜上可得，為了開展維修間隔優化所需抽取的維修任務樣本量為

(4)

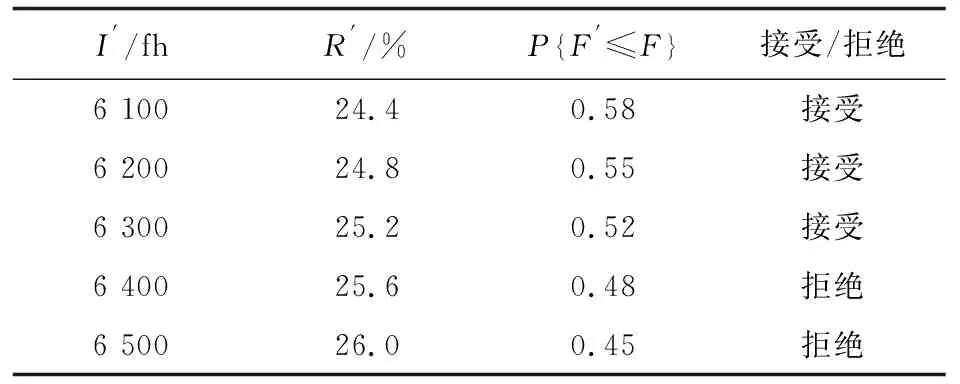
樣本量m是在假設樣本總體足夠大的前提下得到的，當樣本總體S較小(S

(5)

綜上所述，想要對某一項維修任務的間隔進行優化所需的樣本量應至少為n。

對維修任務抽樣后，可以計算維修任務抽樣比例Rt=n/S，假設每架飛機的維修任務數等概率(該假設符合實際情況，因為航空公司一般都會均勻地給每架飛機安排運營，因此，產生的維修需求也是均勻的)，則飛機數抽樣比例Ra=Rt，故飛機的樣本量應為

na=RaNa

(6)

最后，由于一型飛機的服役時間很長，使得航空公司擁有該型飛機的機齡跨度較大，而間隔調整工作影響的是整個型號維修任務，因此需要對不同機齡的飛機進行分層抽樣，進而得到的樣本能夠更真實地反映總體情況。分層抽樣的原理，是基于飛機抽樣比例從不同機齡的飛機總數中進行抽取，得到第i(i=1,2,…,k)種機齡飛機的抽樣數量為

na,i=RaNa,i

(7)

2 判定維修間隔優化的必要性

完成樣本量抽取需要對維修間隔優化的必要性進行初步判定，該步驟需要對維修任務在不同時間段出現的故障數量進行統計分析，并進行趨勢分析，用于幫助預判維修間隔調整對故障數量造成的影響[13]。

鑒于飛機故障的統計是按照飛行小時區間劃分進行的，因此得到的分組統計數據組數較少，例如，以4 000 fh為間距進行分組，則到20 000 fh(以8 fh/天的使用率來計算，此時飛機服役時間已接近10年，需要開展D檢)為止只能得到5組數據。在進行趨勢擬合時建議使用線性回歸，從而更加直觀地表達故障產生的情況。

通過對N組樣本值的飛行小時數和故障數(xi,yi)進行分組統計，令擬合直線為y=a+bx，基于最小二乘法可得擬合直線的參數分別為

(8)

當擬合直線斜率較大時，表明擴展維修間隔導致更多的故障發生，建議嘗試縮短維修間隔；當斜率較小時，表明擴展維修間隔不會明顯增加或減少故障發生的數量，建議嘗試對維修間隔進行適當的擴展。

理論上來講，還存在斜率為負數的可能，表明故障率會隨著使用時間的增加逐步降低，這種情況只有在選用的設備未通過“老煉”的時候才會發生。對于經過嚴格選材和試驗的裝備來說，在實際工程中發生這種情況的可能性非常低。

圖1 故障趨勢分析示意圖

在實際工程中，如果故障趨勢滿足相應制造商的“趨勢”定義，即斜率達到制造商可接受的程度時，便可對該項維修任務的間隔進行相應調整。也就是說，即使斜率為正數時，但只要延長維修間隔后導致可能增加的故障數在可接受范圍內，便認為該任務的間隔可擴展。

3 定義拒絕域及假設檢驗準則

若維修任務的間隔存在優化的必要性，則需給出新的維修間隔I′=I+ΔI，其中ΔI可以為正數或負數。對于新給定的維修間隔，需要通過定義拒絕域對其進行假設檢驗。合理地定義拒絕域是維修間隔優化的關鍵步驟。

由于預防維修的目的是通過定期開展維修活動實現減少故障發生，因此，用故障數與檢查次數的比例R來度量當前維修間隔下維修活動的有效性，故有

R=I×λa×100%=F/N

(9)

式中：I為維修任務的原始間隔，fh；λa為該任務可接受失效率，1/fh，該值是制造商對MSG-3各類故障的可接受失效率；N為任務數；F為故障數。

將維修間隔調整為I′后，新得到的故障發生比例R′應比調整前更低才能表明間隔調整后，維修活動的有效性沒有降低，即滿足R′≤R，其中，R′=I′×λa×100%=F′/N。

假設檢驗為：若間隔調整后故障數量F′比間隔調整前的故障數量F少的概率達到置信程度β，則認為本次間隔調整是有效的，否則重新確定調整幅度。故定義：

(10)

對于故障來說，一般假定其到達服從泊松分布，到達強度表征的是當前間隔下的平均故障數。故調整后故障發生次數的平均值為μ=R′N，因此可以得到原假設的拒絕條件為

P{F′≤F}=P{F′≤RN}=

(11)

4 數值算例

假設某航空公司擁有某型飛機Na=59架，年平均利用率Uy=2 200 fh，針對某項維修任務收集了Ts=6的數據，該任務初始維修間隔為I=6 000 fh，每次檢查能夠發現故障的概率為p=0.15，制造商給出的可接受水平值為p=0.04，則由式(4)可知需要抽取的任務樣本量為m=306條，高于航空公司擁有的任務總數S=130，因此需要對樣本量進行調整。基于式(5)，令z=m-1[14]，得到至少需要抽取的樣本量n=91條，且需要抽取的飛機總量為na=42架。

假設航空公司該型飛機的機齡分布如表1所示，得到在本次維修間隔優化工作中，需要從不同機齡群體中抽取樣本量，將這na=42架飛機的維修數據抽取后，得到最終任務樣本量N=105條。

表1 某型飛機機齡分布情況

表2 某型飛機故障分布趨勢

假設該維修任務是MSG-3分析[15]得到的一個9類任務，則對應故障的可接受失效率為λa=4×10-5，進而得到故障數與檢查次數的比例R=25%。當置信度β=0.5，得到新的維修間隔結果如表3所示，即最大可以嘗試將維修間隔延長至6 300 fh。

表3 間隔延長假設檢驗結果

5 結束語

本文給出一套工程實用的維修間隔優化方法，能夠對維修間隔進行優化。通過適當的維修間隔調整可將本文方法延用到其他類型裝備的預防性維修任務間隔優化工作之中，為該裝備計劃維修要求(SMR)的更新提供支撐。