工業產品表面高精度三維測量方法的研究

孫 亮，韓勇華，王劍濤，王軼驍，朱 漣，伏燕軍*

(1.南昌航空大學，330063，南昌； 2.南昌航空大學無損檢測技術教育部重點實驗室，330063，南昌)

0 引言

隨著數字圖像處理、人工智能以及計算機科學的高速發展，基于條紋投影的三維測量[1-2]方法，由于其具有非接觸、高速、高精度和全場測量[3]等優勢被廣泛應用。目前基于條紋投影的三維測量方法在很多領域有著廣泛應用，例如，安防監控領域[4-5]、生物醫學領域[6-7]以及工業在線監測領域。在條紋投影的三維測量基礎中，通過將預先設計好的正弦條紋由DLP投影儀投射到物體表面，被物體調制后的變形條紋由相機接收并送至計算機，經過求解包裹相位和相位展開得到帶有物體高度信息的相位值，再經過系統標定后就可以得到物體的三維形貌。

傅立葉變換法[8-9]和相移法[10-11]是常見的包裹相位獲取方法。傅立葉變換法求解包裹相位雖然只需一幅條紋圖，但其精度比相移法要低。而相移法對環境光和隨機噪聲不敏感，求解的包裹相位精度高，但是在測量系統中，采集條紋圖使用的DLP投影儀和CCD相機多為非線性設備，正弦條紋不具有較好的正弦性，從而導致求解的相位仍然存在一定誤差。這種非線性效應是影響投影測量系統精度的主要因素。

Jia[12]提出了一種新型高速兩步相移法用于三維測量，該方法只需要投影2個相移180度的三角形條紋圖，通過計算2個捕獲的三角形條紋圖得到強度比就可以對物體進行三維重建。Dai[13]等利用三步相移算法獲得包裹相位時發現測量精度會被存在的高次諧波影響，提出了利用具有周期性和對稱性的二元圖案來產生高質量的條紋圖案。Xu[14]等人為了減輕高次諧波的影響，提出了一種被動誤差補償的方法，但是如果條紋寬度過大，這個方法會受到限制。Flores[15]提出了一種合成三角波條紋的方法，可有效解決投影儀非線性伽馬引起的問題。Huang[16]提出了一種可以明顯地減小該相位誤差的雙三步相移算法，需要2組初始相位差設計為60°的正弦光柵條紋投影圖(每組3幅圖)，相位誤差可以得到明顯的改善，實驗證明，該方法能有效地削弱非線性誤差對條紋投影測量系統的影響。在實際測量中，雙四步相移算法由于相位誤差的正弦周期與相移算法的相移步數有關，且初始相位的差值設計為45°，更能夠有效地減小測量誤差。實際上，系統中存在的噪聲、環境光以及離焦程度等因素都會造成不同程度的相位誤差[17-20]。而基于相位而不是強度的相位編碼方法[21]對環境光、相機噪聲和測量物體表面的對比度等因素不敏感，具有良好的抗干擾能力和較強的魯棒性。由于雙四步相移算法[22]仍然具有四步相移算法抗噪性的優點，從中得到的融合相位[22]需進行相位展開，提出了一種雙四步相移結合相位編碼的三維測量方法，較于傳統的相移結合相位編碼的方法，該方法可以進一步抑制非線性誤差對測量帶來的影響，提高測量的精度。實驗結果表明了該方法的可行性和有效性。

本文其余部分結構如下。第1部分介紹了雙四步結合相位編碼的原理。第2部分通過實驗證實方法的可行性。第3部分總結本文。

1 原理

1.1 測量系統原理

如圖1所示為基于結構光的三維測量系統，該系統由投影儀、工業CCD相機、計算機、參考平面組成。相機光軸與參考平面垂直，然后投影儀光軸和相機光軸相交于參考平面上的O點，P為投影儀光心點，C為相機光心點，兩點在同一高度，d為兩點之間的距離，兩點到參考平面的距離為l。其中參考平面上正弦條紋頻率為f，物體表面圖像和參考平面圖像對應點的連續相位差為△φ。則下列計算公式(1)是被測物體某點M的高度：

(1)

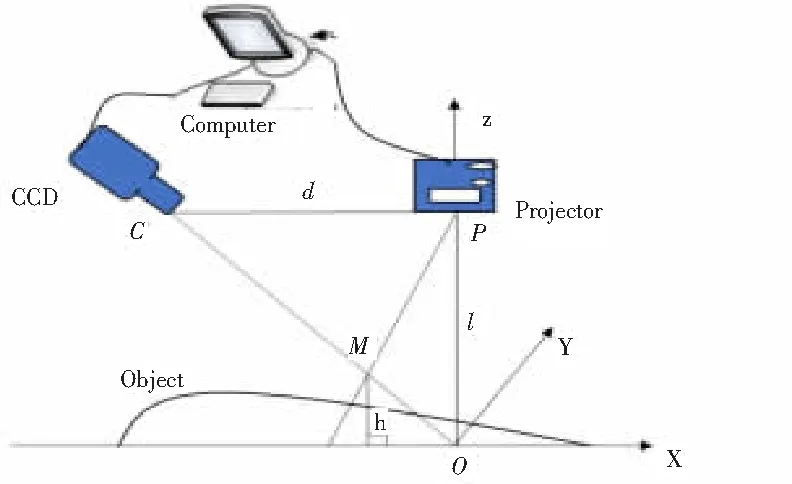
圖1 三維測量系統原理圖

1.2 雙四步相移原理

針對N步相移算法[23]的第i個正弦條紋圖案可以表示為：

Ii(x,y)=Ia(x,y)+Ib(x,y)cos[φ(x,y)+δi]

(2)

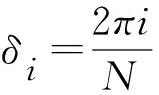
對待求相位φ(x,y)進行傅立葉級數展開獲得實際相位φ′(x,y)，則△φ(x,y)=φ′(x,y)-φ(x,y)，根據三角函數獲得：

(3)

則相位誤差相位函數△φ(x,y)為：

(4)

傳統的四步相移算法所對應的相位誤差函數可以近似表示為：

△φ(x,y)≈c1sin[4φ(x,y)]

(5)

式中c1為一個常數。

在投影N幅正弦條紋圖中，外加一個初始相位?，設計好的正弦條紋圖則可以描述為：

Ii(x,y)=Ia(x,y)+Ib(x,y)cos[(φ(x,y)+?)+δi]

(6)

式中：[φ(x,y)+?]為上述正弦條紋圖的初始相位。則此時的四步相移算法中，可以近似表示相位誤差為：

△φ′(x,y)≈-c2sin{4[φ(x,y)+?]}=-c2sin[4φ(x,y)+4?]

(7)

當條紋圖未引入額外的初始相位，即?=0時，實際相位分布對應的相位誤差為△φ(x,y)，此時的實際相位可表示為：

(8)

而當?=π/4時，相位誤差為：

△φ′(x,y)≈-c2sin[4φ(x,y)+4×π/4]=c2sin[4φ(x,y)]=-△φ(x,y)

(9)

則可以由2種形式表示此時實際主值相位分布：

(10)

(11)

(12)

1.3 相位編碼原理

Wang在2012年首次提出相位編碼[24]的方法，利用一組正弦條紋和一組相位編碼條紋即可實現相位解包裹，使用相位代替強度來確定碼字，增強了其魯棒性。相位編碼方法中的編碼相位需預先設計好并嵌入到相位編碼條紋中去，通過一系列計算可確定條紋級次，求得條紋級次與包裹相位的周期一一對應。傳統相位編碼原理流程如圖2所示。

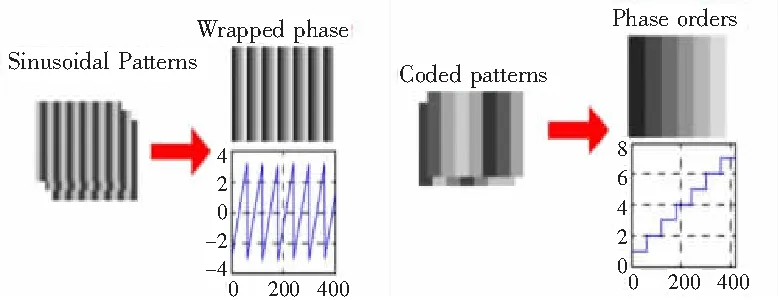
圖2 相位編碼原理流程圖

1)設計階梯編碼相位，初始相位由式(13)生成：

(13)

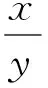
2)根據式(14)生成相位編碼條紋：

Ak(x,y)=a(x,y)+b(x,y)cos[φs(x,y)+2π(k-1)/4]

(14)

式中：a(x,y)是平均強度，b(x,y)是調制強度，這里，k=1、2、3、4。

正弦條紋圖案和相位編碼條紋圖案如圖3所示。

(a)四步相移條紋 (b)相位編碼條紋圖

3)從相位編碼條紋圖中獲得被編碼在-π到+π的范圍內的階梯相位φs(x,y)。階梯相位可利用式(15)計算獲取：

(15)

4)根據獲取的階梯相位確定條紋級次k(x,y)：

k(x,y)=Round[N(φs(x,y)+π)/2π]

(16)

式中Round[·]為確定最接近的整數。

5)條紋級次k(x,y)確定后，就可以進行相位展開。根據式(17)將包裹相位φ(x,y)轉換為絕對相位Φ(x,y)。

Φ(x,y)=Φ(x,y)+2π×k(x,y)

(17)

2 實驗

為了驗證該方法的性能，搭建了一個測量系統，包括一個投影儀(DLP Light Crafter 4500)、一個CMOS攝像機(Basler acA1600-20gm GigE)和一臺計算機，如圖4所示。投影儀分辨率為1 140×912，攝像機分辨率為1 280×1 024。在接下來的實驗中，正弦條紋圖和相位編碼圖選擇周期為32個像素。系統采用參考文獻[25]中的方法進行標定。

圖4 三維測量系統圖

2.1 模型測量實驗

為了驗證本方法的可行性，測量了一個烏龜玩具模型。在實驗過程中，相移步數N取4，由計算機得到的四步相移正弦條紋圖案和四步相位編碼圖案被依次投影到待測的烏龜玩具模型的表面上，并且烏龜玩具模型調制的條紋圖像用相機順序地采集。其中，圖5(a)是模型的四步相移正弦條紋圖案的其中1幅，圖5(b)為4幅相位編碼條紋圖的其中1幅，從中可以計算出整數型編碼相位。如圖5(c)所示是通過雙四步相移可以獲得融合相位。條紋級次k(x,y)從被調制后的相位編碼圖案中計算出，圖5(d)為融合相位和條紋級次圖的某一行。最終，通過高度公式，如圖5(e)和(f)所示可以獲得烏龜玩具模型的三維重建結果。從圖5中可以看出，在烏龜玩具的模型眼睛部位和背部有一些凹凸不平區域，也同樣可以被很好地復原出來。

(a)四步相移條紋圖的其中1幅 (b) 4幅相位編碼條紋圖的其中1幅

3 結論

基于傳統的相移結合相位編碼的方法，由于系統中非線性響應的影響，所測得的相位信息存在誤差，降低了測量精度。提出的一種雙四步相移結合相位編碼的三維測量方法，只需投影傳統相移算法2倍相移光柵的雙四步相移算法具有四步相移算法良好的抗噪性優點，2幅包裹相位圖通過2次四步相移算法計算獲得，經過相位融合得到融合相位。而相位編碼的方法對環境光以及系統的噪聲等因素具有較好的魯棒性，對條紋級次的準確判斷有利，可以獲得比較理想的測量精度。相對于傳統的相移結合相位編碼的方法，該方法可以進一步抑制條紋投影輪廓術非線性測量誤差對測量帶來的影響。綜上所述，該方法能對孤立復雜物體進行測量，且容易實現，更加有效，實驗表明了該方法的可行性。