基于EM算法的混合線性回歸模型的應用研究

范曉東，崔 瑩，張慶春

(1．吉林化工學院 理學院，吉林 吉林 132022；2．遼寧師范大學 數學學院，遼寧 大連 116029)

近年來,有限混合模型[1]得到了學者廣泛關注,已知樣本觀測數據來自于一些不同的類，但是每個類的比例是缺失的，有限混合模型經常被用來對這類數據進行建模．EM算法[2]作為一種迭代算法，是處理有限混合模型的一個重要算法．本文用EM算法來求解帶有刪失數據[3-4]的混合線性回歸問題，建立了混合線性回歸模型[5]的參數估計程序并對國民生產總值數據集進行了分析．

1 線性混合模型

(1)

(2)

(3)

(4)

和

(5)

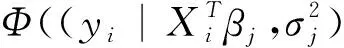
2 混合回歸的EM算法

1.E步驟

計算Q(θ|θ(t))，也就是計算組分包含的“后驗”概率(以數據和θ(t)為條件)，則對于i=1,2,…,n,j=1,2,…,m，

(6)

2.M步驟：

(1)對于參數λ，設

(7)

重復上面的步驟1、2直至收斂.

3 實例分析

收集了2019年46個國家的人均國民生產總值和人均二氧化碳排放量的數據建立數據集，該數據集包括2019年人均國民生產總值(GNP)和2019年人均二氧化碳(CO2)排放量，主要討論兩者之間的關系.使用模型(1)來建立人均國民生產總值關于人均二氧化碳排放量的混合線性回歸模型，對于模型(1)采用分兩類的情況，使用第二節中的程序得到混合線性回歸模型為：

(8)

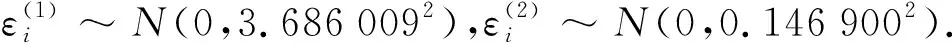
圖1展示了回歸曲線及其99%的置信帶．圖1表明使用兩個組分的混合回歸來擬合數據集是合理的，而且對于GNP較低的國家來說，如果將來他們想增加GNP有(8)式中的兩種方案可供選擇．

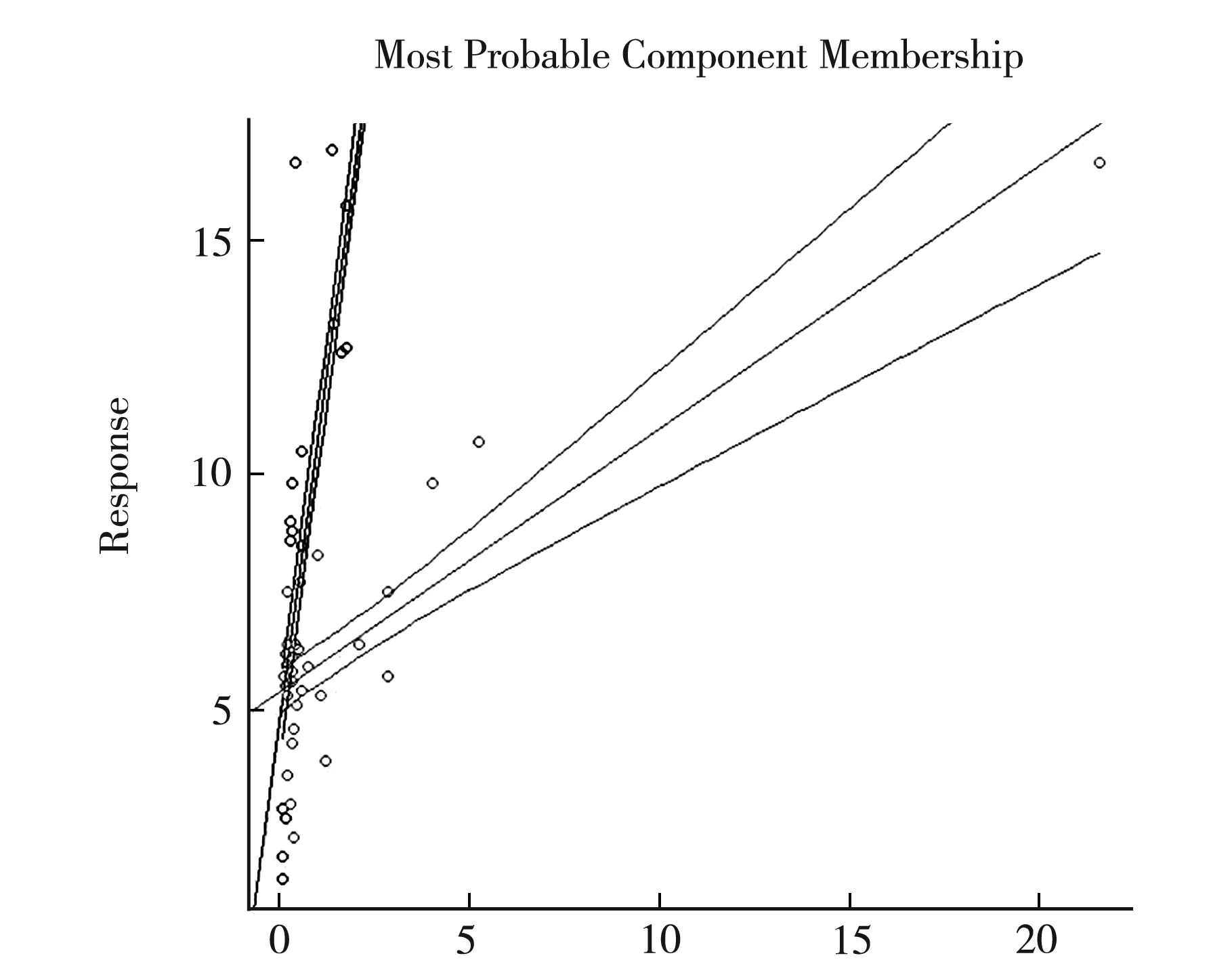
Predictor圖1 回歸曲線

4 結 論

研究了帶有刪失數據的混合線性回歸模型的參數估計問題，并且利用EM算法建立了混合線性回歸模型的估計程序．收集2019年46個國家的人均國民生產總值和人均二氧化碳排放量的數據建立數據集，利用混合線性回歸模型來分析這個數據集，得出使用兩個組分的混合回歸來擬合數據集是合理的，并且得到了回歸方程，為低GNP國家增加GNP提供了兩種選擇方案．