基于Optistruct的電池包箱體上蓋優化設計

譚麗輝,劉 慶,李春陽

(1.吉林化工學院 機電工程學院，吉林 吉林 132022；2.北方華錦化學工業股份有限公司 雙興工程塑料分公司，吉林 吉林 132022)

動力電池作為純電動汽車唯一的能量來源，對整車性能影響尤為重要，通常由于車身空間限制，懸掛在汽車底盤下方.電池箱是動力電池系統的唯一載體，對電池系統的安全工作和防護起著關鍵作用.電池箱多為薄板件，常常面對顛簸、剎車和碰撞等復雜路況的考驗，則其箱體結構設計的合理性即成為首要任務[1-10].

基于ANSYS Workbench平臺，結合實際工況對電池包箱體進行靜、動態有限元分析，判斷箱體結構的薄弱位置，在上蓋表面設置凸包結構進行局部加強，運用Optistruct軟件的形貌優化技術，對箱體上蓋的局部剛度進行優化，得到凸包結構的幾何參數和平面布局，并構建了優化后箱體上蓋的三維模型.

1 箱體有限元分析

1.1 有限元模型構建

圖1為某款電池包結構示意圖，整個電池包呈較規則的長方體.為了正確模擬力的傳遞路徑，將復雜的電池模組簡化為較規則的方形體，同時將簡化的電池模組引入到電池包箱體，并將上蓋作透明處理，如圖2所示，作為后續電池包箱體有限元分析模型.

圖1 電池包結構示意圖

圖2 電池包簡化模型

基于ANSYS Workbench軟件的網格剖分和接觸自動識別技術，采用solid185單元在箱體厚度方向布置2層網格，單元尺寸為20×20 mm，進行箱體結構模擬.

考慮在極端工況下，材料會出現大變形，而DC01材料具有完備的彈性階段和塑性階段本構關系，表1給出DC01材料屬性.

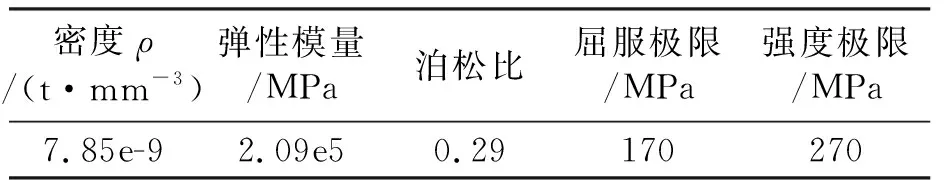
表1 DC01材料屬性

在電池包箱體的兩側掛點上施加約束，如圖2所示圓圈標記處.采用的實體單元只具備3個平動自由度，故對掛點表面上的節點也僅約束3個平動自由度.

為了考察電池包箱體結構是否能夠保護內部電池模組和電氣連接安全，選擇了不同典型工況對箱體做靜態有限元分析.表2給出了典型靜態工況及加載方式(已包含重力加速度).

表2 典型工況及加載方式

1.2 靜態有限元分析結果

在ANSYS Workbench中利用靜力學模塊可求得上述3種典型工況下電池包的變形分布情況.圖3分別給出了3種工況下，電池包的變形情況.在急剎車工況下，下箱體前后受力明顯，但沒有發生明顯的變形，最大變形量僅為0.08 mm；在顛簸工況下，箱體上蓋受力明顯，最大變形量達到22.65 mm；在顛簸和急轉彎組合工況下，箱體上蓋依舊為主要受力區，最大變形量為22.66 mm，與顛簸工況相比，急轉彎對箱體上蓋變形的影響有限.綜上可見，在顛簸工況下箱體上蓋受力較大，產生較大的變形量，下文的優化設計，將以此作為極限工況進行對比分析，評價上蓋優化效果.

(a)急剎車工況的Y向位移云圖

(b)顛簸工況的Z向位移云圖

(c) 顛簸+急轉彎工況的總位移云圖圖3 典型工況的位移云圖

根據電池箱靜力學特性評價標準[11]：(1)在1 g加速度下，構件的變形量不應超過1 mm；(2)在3 g加速度下，構件的變形量不應超過3 mm.由靜態有限元分析結果可見，箱體上蓋是剛度薄弱件，需進行改進優化設計.

1.3 模態分析結果

在車輛實際行駛過程中，電池包的受力是復雜多變的，對其動態特性的研究是必不可少的，最主要的是模態分析.

基于Lanczos方法，提取箱體結構的前六階固有頻率，其中前三階固有頻率均低于30 Hz，一階固有頻率僅為13.66 Hz，發生共振的風險較大.由前六階振型圖4可見，共振區域均發生在箱體上蓋，分別存在1～4處共振區域不等，上蓋均呈現不同形式的上下振動，發生彎曲變形，可見其動剛度不足，亟待加強.

(a)一階模態

(b) 二階模態

(c)三階模態

(d) 四階模態

(e) 五階模態

(f) 六階模態圖4 電池包箱體模態分析結果

通常路面激勵頻率f其表達式式為：

式中：V為車輛行駛速度，單位為km/h；λ為路面不平度波長，單位為m.

為避免共振情況發生，箱體上蓋一階頻率需高于路面的激勵頻率.表3給出了3種常見路面對應的激勵頻率，可見，由路面不平度產生的激勵頻率最高為27.78 Hz，而箱體上蓋一階固有頻率僅為13.66 Hz，優化后箱體上蓋的一階頻率只需高于27.78 Hz，即滿足設計要求.

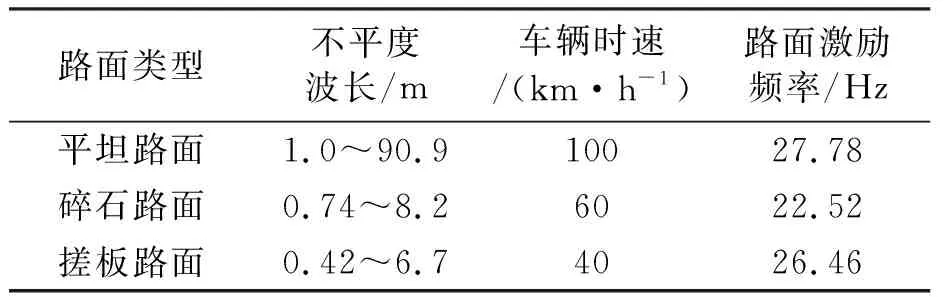
表3 不同類型路面的激勵頻率

2 上蓋形貌優化設計

2.1 上蓋簡化有限元計算

為改善箱體上蓋剛度嚴重不足的情況，通常在箱體上蓋采用鈑金沖壓方法加工出凸包結構.為簡化計算將箱體上蓋從電池包模型中單獨抽離出來，其中上蓋平板為優化區域，而與下箱體相接的帶螺栓孔的折彎結構，為非優化區域，圖5為簡化的箱體上蓋有限元模型.在顛簸工況下對其進行靜力學和模態計算，并與前文進行對比，以驗證該簡化方法的有效性.圖6給出了簡化上蓋的位移云圖，最大變形處仍發生在上蓋中心，變形量為20 mm，與前文詳細模型計算結果較為接近；對比表4可知，兩種模型前六階固有頻率極為接近，最大相對誤差僅為1.12%，故上蓋簡化模型完全可以替代上文電池包的詳細模型進行優化設計.

圖5 上蓋的有限元模型

圖6 顛簸工況下的位移云圖

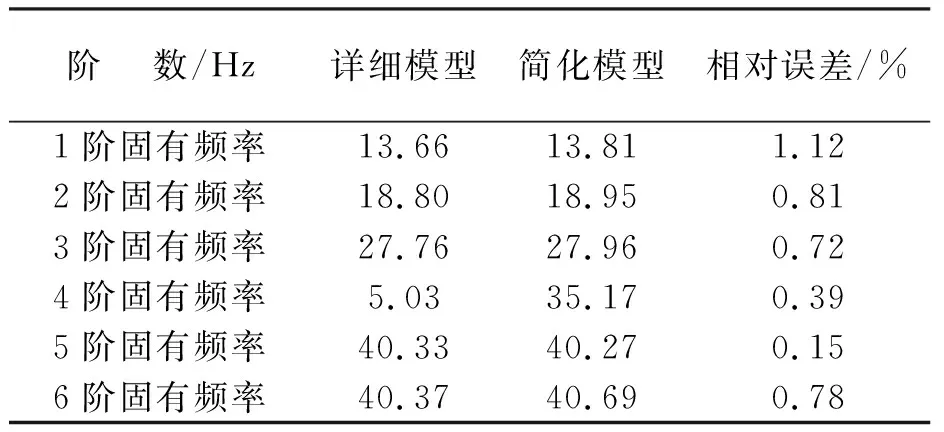
表4 簡化模型與詳細模型固有頻率對比

2.2 上蓋優化設計

將上蓋中心部分節點的靜態位移、上蓋的一階固有頻率和體積定義為優化響應；將凸包的最小寬度設為40 mm，拔模角設為70°，最大沖壓高度設為10 mm；將上蓋中心部分節點位移上限定為11 mm，可保證在瞬時加速下上蓋不會與電池模組發生碰撞，一階固有頻率下限設為28 Hz(前文平坦路面產生的激勵頻率最高，為27.78 Hz).以總體積最小為目標，進行上蓋的優化設計.

靜態位移和一階固有頻率經過25次迭代計算后收斂，兩者均能滿足給定的參數要求，圖7即為優化后箱體上蓋形貌圖.可見，優化后上蓋凸包結構基本呈對稱分布，即左右兩側的E型凸包和前后的矩形凸包.其中，E型凸包高度大約為5～6 mm，矩形凸包厚度基本達到了最大約束值10 mm.

圖7 優化后上蓋形貌

依據優化后的上蓋形貌云圖并結合單元尺寸，可提取出E型和F型兩種凸包結構的幾何參數，其中E型凸包高度設定為6 mm，矩形凸包高度設定為10 mm，拔模角均定為70°.如圖8、9所示采用Solidworks三維建模軟件構建凸包結構，改進后箱體上蓋三維模型如圖10所示.

圖8 矩形凸包結構

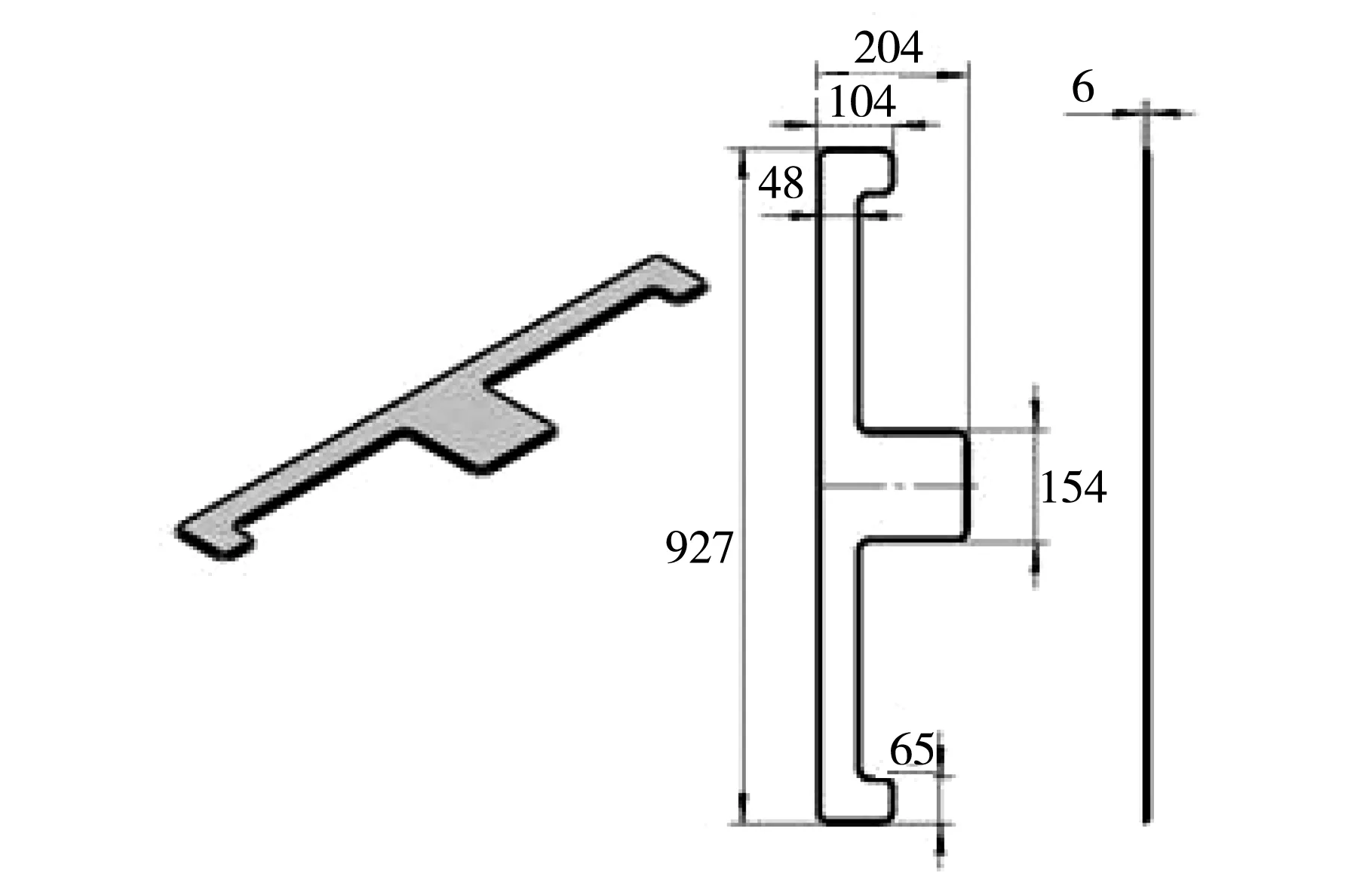
圖9 E型凸包結構

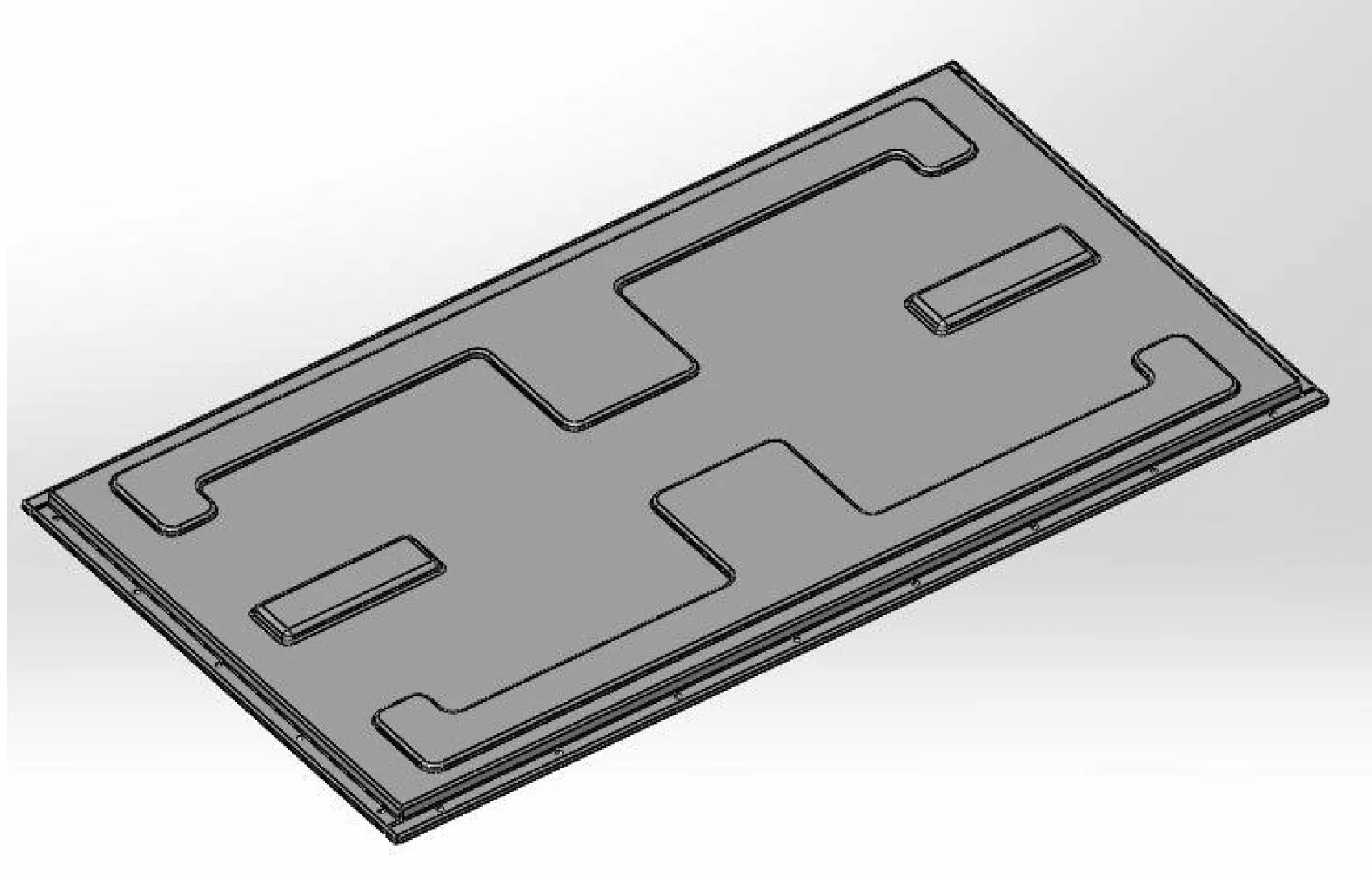
圖10 優化后上蓋三維模型

2.3 上蓋優化效果分析

改進后上蓋的固有頻率較原模型有較大提高，平坦路面激勵頻率均低于一階固有頻率，滿足設計要求，可以避免共振情況發生.由顛簸工況下優化后上蓋的位移云圖和應力云圖11、12可見，最大變形位于上蓋中心，變形量為5.66 mm，較優化前降低了72%，剛度改善效果明顯，達到設計要求；最大等效應力落在E型凸包前后兩側角點，僅為101 MPa，明顯低于材料的屈服極限，強度提升顯著.

圖11 顛簸工況下優化后上蓋的位移云圖

圖12 顛簸工況下優化后上蓋的應力云圖

3 結 論

基于ANSYS Workbench軟件，對電池包進行靜、動態有限元分析，得到箱體結構的薄弱位置，在上蓋表面設置凸包結構進行局部加強；并采用Optistruct軟件，運用形貌優化技術，以動剛度和靜剛度為約束指標，獲得矩形凸包和E型凸包的結構布局和幾何參數，結合Solidworks三維建模軟件，建立了優化后箱體上蓋的三維模型.經驗證，優化后上蓋最大變形量較優化前降低了72%，僅為5.7 mm，一階固有頻率提升至28.55 Hz，可避免共振情況發生，最大等效應力減小至101 MPa，遠遠低于材料的屈服極限，可見優化后上蓋的剛度、強度均得到顯著提升.