基于多尺度熵的Duffing 混沌系統閾值確定方法*

黃澤徽 李亞安 陳哲 劉戀

(西北工業大學航海學院, 西安 710072)

1 引 言

混沌系統的初值敏感性和噪聲免疫性使它在微弱信號檢測領域得到了廣泛的關注, 為微弱信號的檢測提供了新的思路. 美國的Birx 博士在他的博士論文中最先提出將混沌理論應用于弱信號的檢測. 王冠宇等[1]在國外學者研究工作的基礎上,利用Duffing 振子對白噪聲背景下的微弱正弦信號進行了檢測研究, 實現了對頻率已知的待測信號幅值的估計, 檢測信噪比可以達到–26 dB, 推動了信號檢測領域的發展. 李月等[2?5]研究了強噪聲下混沌振子對微弱正弦信號、方波信號的檢測, 色噪聲背景下混沌振子對微弱正弦信號、方波信號的檢測, 指出混沌振子系統對零均值噪聲具有很強的免疫力. 之后大量學者對Duffing 檢測系統進行改進,賴智慧等[6]對基于Homles-Duffing 振子的混沌檢測進行了改進, 提出變尺度微弱信號檢測方法; 叢超等[7]提出了一種基于適應步長型間歇混沌振子的信號檢測方法, 用一個振子系統可以實現對任意頻率任意相位的微弱周期信號的搜索檢測; 牛德智等[8]針對同頻微弱信號檢測時存在的盲區, 提出了一種策動力移相法予以消除; 陳志光等[9]利用間歇混沌現象對頻率未知信號進行檢測并取得較好的效果; 時培明等[10]提出了一種基于雙耦合Duffing混沌振子與變尺度相結合的微弱信號檢測新方法,將其用于檢測任意多頻微弱信號具有明顯優勢.通過大量學者的不懈努力, Duffing 檢測不斷趨于成熟.

Duffing 混沌系統提供了與傳統方法不同的檢測途徑, 在實際應用中, 混沌系統躍變閾值的確定是利用Duffing 系統準確進行微弱信號檢測的關鍵, 但是傳統的時序圖方法不利于計算機的自動處理. Lyapunov 指數法算法復雜, 且容易受到噪聲的影響. 近年來有大量學者對閾值求解方法進行了研究, 提出了相圖分割法[11]、二分法[12]、0-1 方法[13,14]、基于龐加萊界面的定量判別方法[15]等來計算混沌系統躍變閾值, 但仍具有一定的局限性. 本文將熵引入到閾值求解, 熵可以用來表征信號復雜度, 已有不少學者利用熵對信號復雜度進行分析, 梁滌青等[16]利用小波包能量熵來判斷混沌序列的復雜度;楊孝敬等[17]利用模糊近似熵對磁共振信號復雜度進行分析; 陳祥龍等[18]利用多尺度樣本熵對壓縮機工作時的振動信號進行了分析; 王鴻姍等[19]利用小波包樣本熵通過分析聲信號的復雜度進行異常音提取. 本文發現Duffing 系統在不同狀態下多尺度熵的明顯差別, 利用這一現象通過分析系統多尺度熵與策動力幅值的變化關系, 提出一種基于多尺度熵的Duffing 混沌系統躍變閾值確定方法, 并通過仿真計算說明其可行性.

2 Duffing 混沌系統微弱信號檢測原理

Duffing 振子檢測系統模型為:

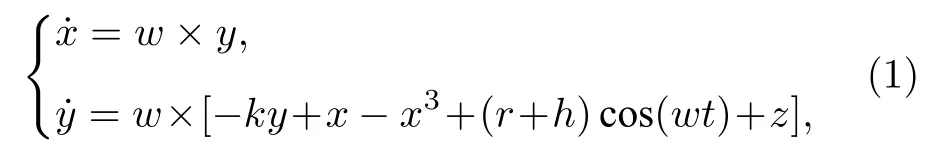
其中k是阻尼比;x?x3是非線性恢復力;rcos(wt)是周期性策動力,r是策動力幅值,h是目標信號的幅值,w是待測信號的頻率,z為白噪聲.

調節策動力幅值使r從0 逐漸增大, 系統將會遍歷同宿軌道狀態、分叉狀態、混沌狀態、臨界混沌狀態, 當r大于某一值rd時, 系統由臨界混沌狀態進入大尺度周期狀態, 相軌跡圖將發生明顯的變化, 如圖1 所示, 其中rd便是本文所要求解的混沌系統躍變閾值. 使用Duffing 混沌系統檢測微弱信號正是基于這一躍變現象: 將系統的策動力幅值r調為rd, 再將待測信號添加到系統, 觀察待測信號添加前后系統的相軌跡是否發生躍變, 如果發生了躍變則說明待測信號中有目標信號的存在. 可知利用這一現象檢測微弱信號時, 躍變閾值的確定非常關鍵, 躍變閾值選取過小, 將會嚴重影響到系統的檢測信噪比; 躍變閾值選取過大, 會導致系統狀態發生躍變, 造成對檢測結果的誤判.

現有計算混沌系統躍變閾值的方法存在一定的局限性, 直觀的相軌跡分析方法簡單直觀、判別方便并且不需要復雜的計算, 但是該方法受到諸多因素的影響, 并且在判別過程中會受到實驗人員主觀因素的影響, 精度低誤差大; Melnikov 和Shilnikov方法可以計算Duffing 系統的混沌范圍, 但是都只能說明當策動力幅值處于這個范圍時, 系統可能處于混沌狀態, 而不能確定系統一定處于混沌狀態;Lyapunov 指數用來度量動力學性態的規則性程度, 描述了系統軌跡收斂或發散的比率, 但是精確的Lyapunov 指數難以得到且容易受到噪聲的影響. 為此本文基于多尺度熵提出一種簡單有效的計算系統躍變閾值的方法.

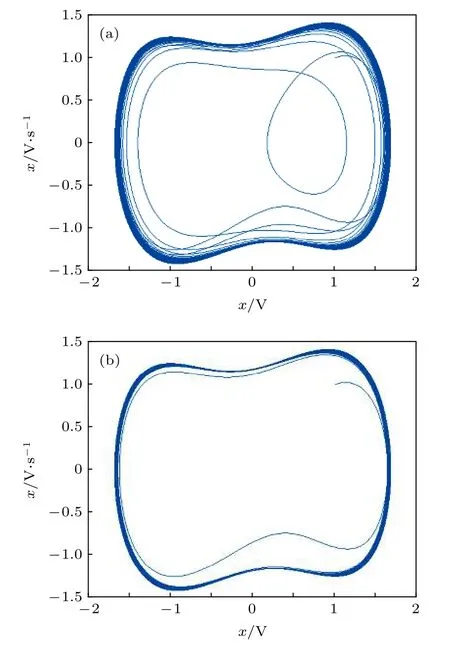
圖1 系統狀態躍變 (a) 臨界混沌狀態; (b) 周期狀態Fig. 1. System state transition: (a) System state transition;(b) periodic state.

3 基于多尺度熵的混沌系統躍變閾值確定方法

熵是系統混亂或無序程度的度量, 系統混亂或者無序的程度越高, 熵值越大, 反之越小. 分析熵值隨策動力幅值變化關系后發現, 系統由混沌狀態進入周期狀態后, 系統熵值明顯變小且趨于平穩,本文利用該現象基于多尺度熵((multi-scale sample entropy, MsEn)來求解系統躍變閾值.

3.1 多尺度熵算法

多尺度樣本熵(MsEn)用于描述在不同尺度上時間序列的無規則程度, 包含參數m,s,τ, 其中m是嵌入維數,s是相似系數,τ是尺度因子. 多尺度樣本熵由兩部分構成: 一是對輸入的時間序列按照尺度τ進行粗細化操作得到新的時間序列; 一是計算尺度τ下新時間序列的樣本熵(sample entropy,SampEn). 具體步驟為[20]:

步驟1對原始時間序列按照尺度τ進行粗細化操作

假定有一離散時間序列x1,x2,x3,··· ,xM共有M個點, 在尺度為τ時對時間序列進行粗-斷點變換得到新的時間序列為:

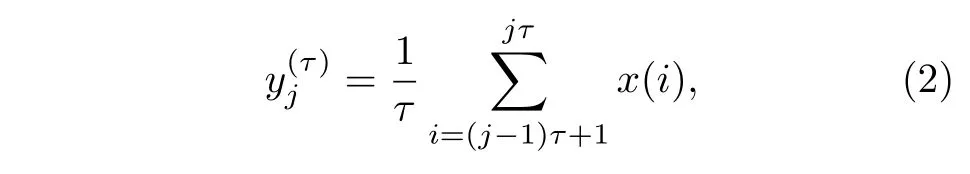
經過粗-斷點變換后得到的新時間序列長度為N=M/τ.

步驟2計算尺度τ下新時間序列的樣本熵

1)將新的時間序列從Y(τ)(1)到Y(τ)(N?m+1)組成一組m維矢量, 第i個矢量Y τ(i) 為:

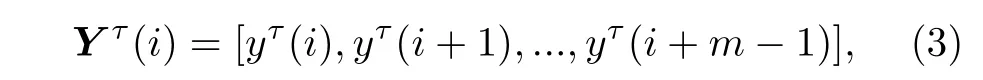
式中i=1～N ?m+1 .

2)定義d[Y τ(i),Y τ(j)]為矢量Y τ(i) 與矢量Y τ(j) 對應元素中差值最大的一個, 即:

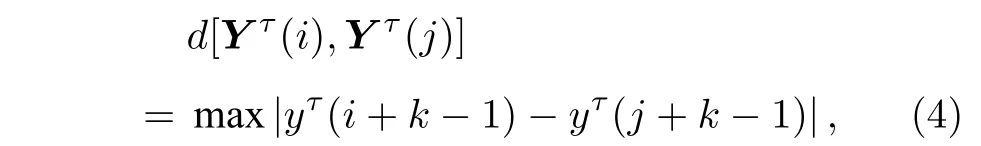
3)給出相似系數s, 計算的數目Di, 及該數目與總的矢量數目N ?m的比值, 記作

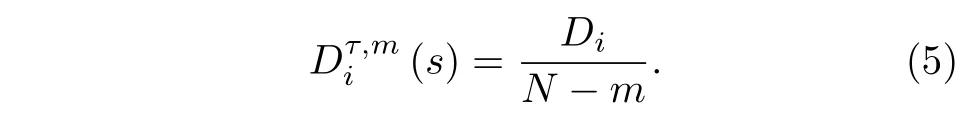
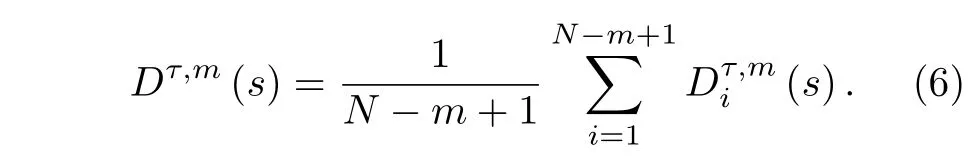
4)將嵌入維數變成m+1 , 重復前面的過程,得到和

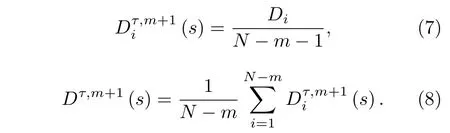
5)時間序列為有限長時, 得到在尺度τ下的樣本熵為

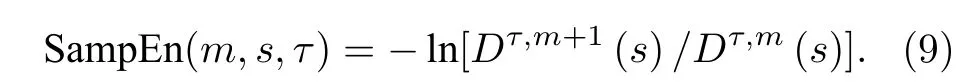
對原始時間序列計算每個尺度τ所對應的樣本熵值, 得到多尺度樣本熵的計算公式為

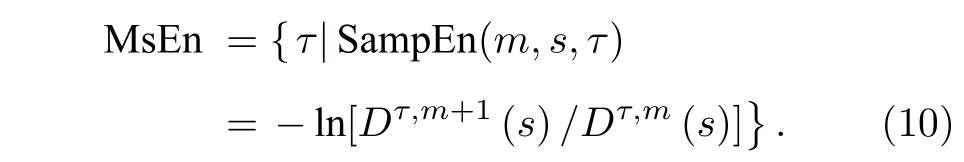
3.2 閾值求解

研究中發現系統混沌態和周期態輸出的時間序列多尺度熵值明顯不同, 且當系統進入周期態后, 系統輸出序列的多尺度熵趨于平穩, 基于此通過描述系統多尺度熵值隨策動力幅值變化情況可以確定系統躍變閾值.

3.2.1 方波信號檢測系統躍變閾值求解

求解方波信號檢測系統的躍變閾值, 系統所采用檢測方程為:

我想我當時的樣子一定很傻，一定呆得像只木雞，但你知道的，在那個愛做夢，對漂亮女孩想入非非的年齡，一般人應該都是這種反應的。

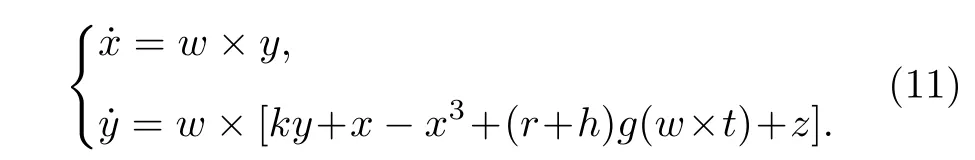
取w= 1 rad/s,k= 0.5, 初值x0= (1, 1), 時間序列長度N= 30000, 尺度因子t= 10, 嵌入維數m= 2, 相似容限s= 0.1SDx(時間序列標準差), 分析多尺度熵值隨策動力幅值r變化情況如圖2 所示. 對圖2 進行分析可知, 系統策動力幅值r?0.605 , 多尺度熵值較大且會隨著策動力幅值r波動,r >0.605 后多尺度熵值趨于平穩且較之前明顯變小, 根據熵的含義及系統變化規律可以判定r >0.605 后系統處于周期狀態, 所以確定該系統的躍變閾值為rd=0.605. 注意在r=0.603 時, 系統多尺度熵值為極小值, 如果只以熵值的大小作為評判標準, 忽略平穩性的評判, 會認為此時系統已處于周期狀態, 但從圖中可以看到此時系統熵值并未趨于平穩, 在之后系統的熵值仍在波動, 所以僅根據熵值大小來求解閾值并不準確. 對該系統進行仿真實驗, 通過分析系統相軌跡圖對比該方法計算結果的準確性, 結果如圖3 所示, 策動力幅值r =0.605 時系統處于左圖所示的混沌狀態, 幅值增加到0.606 時系統便躍變至右圖所示的周期狀態, 通過仿真實驗確定的系統躍變閾值為0.605,多尺度熵方法所求結果與其一致. 可見, 多尺度熵方法可以準確確定方波信號檢測系統躍變閾值.

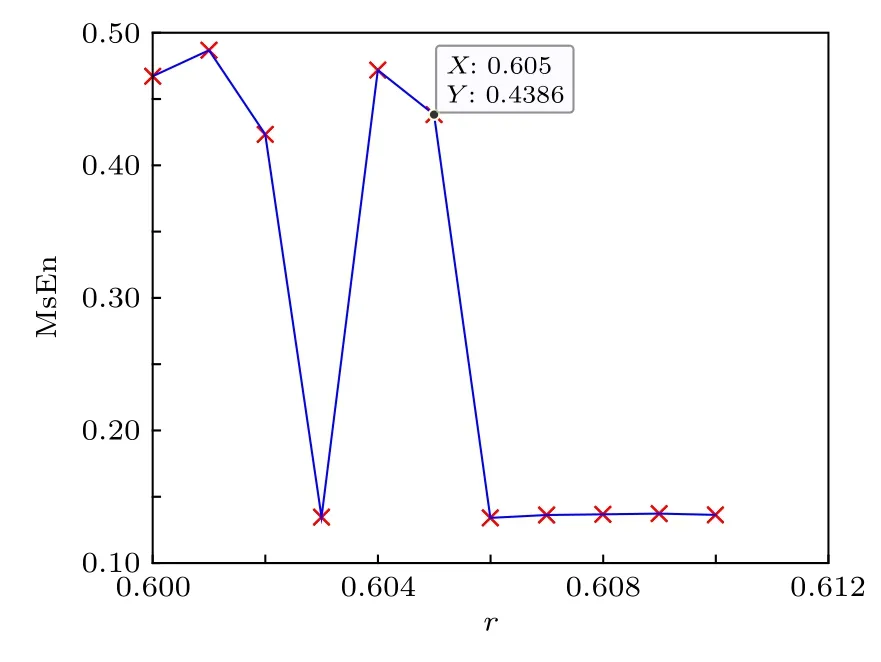
圖2 方波信號檢測系統多尺度熵變化情況Fig. 2. Variation of multi-scale entropy in square wave signal detection system.

圖3 仿真實驗求解方波信號檢測系統閾值Fig. 3. Simulation experiment to solve the threshold of square wave signal detection system.

3.2.2 正弦信號檢測系統躍變閾值求解

求解正弦信號檢測系統的躍變閾值, 利用Duffing 系統(1)式, 取w = 1 rad/s, k=0.5 , 初值x0= (1, 1), 對于多尺度熵算法取時間序列長度N = 30000, 尺度因子 τ=10, 嵌入維數 m=2 ,相似容限 s=0.1SDx, 分析該系統多尺度熵值隨策動力幅值r 變化情況, 結果如圖4 所示, 可知該系統的躍變閾值為 rd=0.826 . 通過圖5 所示的仿真實驗可以確定該系統的閾值為0.826, 與多尺度熵方法所求結果一致.

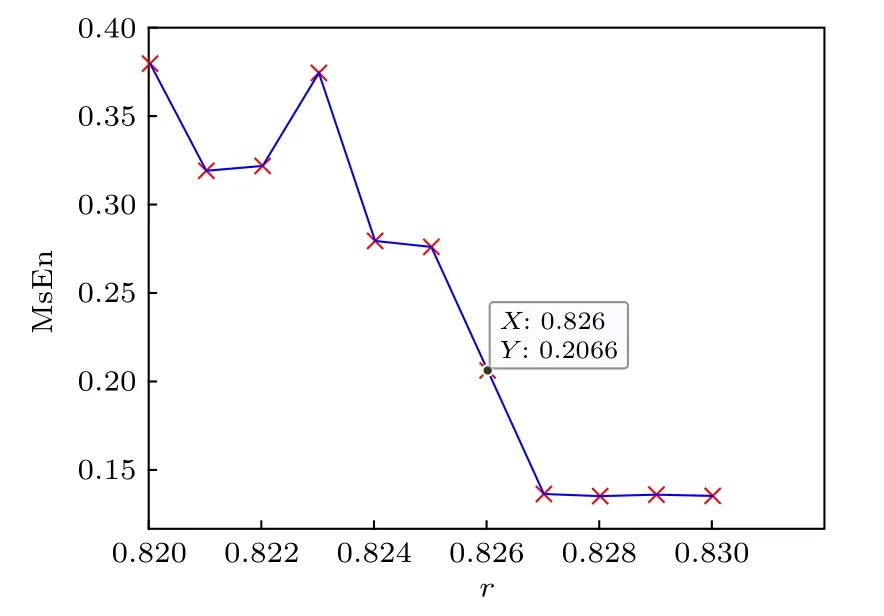
圖4 正弦信號檢測系統多尺度熵變化情況Fig. 4. Variation of multi-scale entropy in sinusoidal signal detection system.

圖5 仿真實驗求解正弦信號檢測系統閾值Fig. 5. Simulation experiment to solve the threshold of sinusoidal signal detection system.

3.2.3 真實信號檢測系統躍變閾值求解

為了驗證多尺度熵方法對真實信號檢測系統的閾值求解效果, 選取一組真實的艦船信號作為樣本數據, 真實待檢測信號的波形如圖6 所示, 頻域波形如圖7 所示, 分析可知真實水聲信號包含頻率為50.27 Hz 的正弦信號. 在系統中內置頻率為50.27 Hz 的正弦信號, 求得該系統閾值為rd=0.825 ,結果如圖8 所示, 進行仿真實驗也得到rd=0.825的閾值, 如圖9 所示.

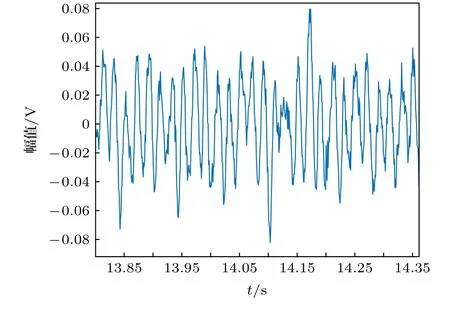
圖6 真實水聲信號Fig. 6. Real underwater acoustic signal.

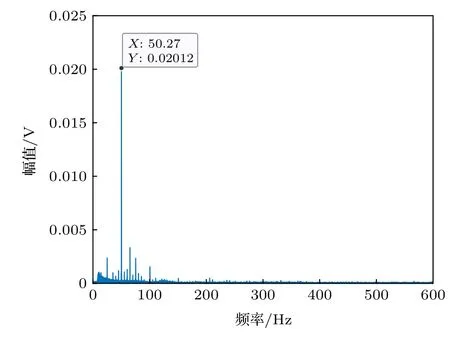
圖7 真實水聲信號頻譜Fig. 7. Spectrum of real underwater acoustic signals.

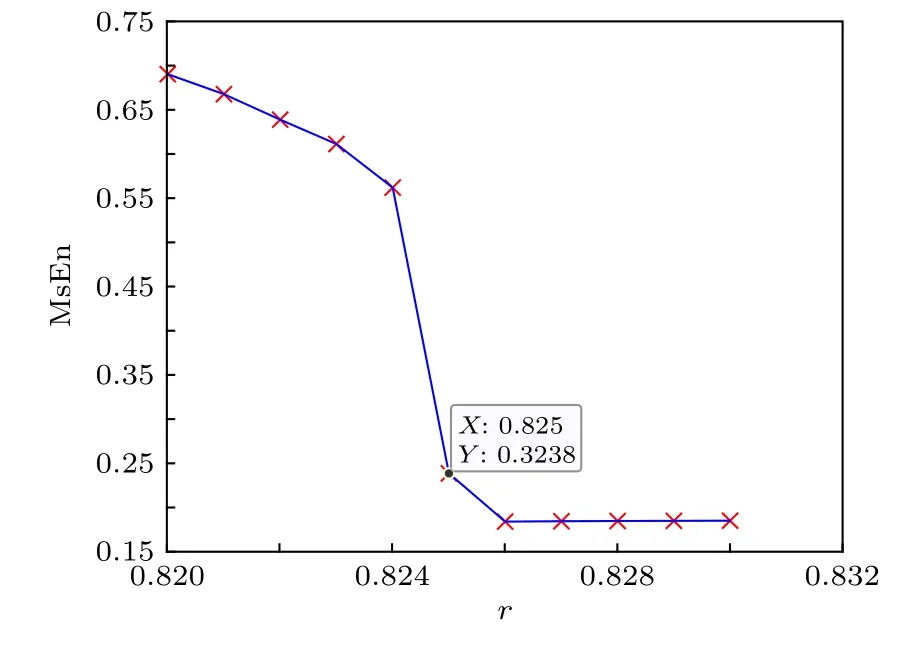
圖8 真實信號檢測系統多尺度熵值變化情況Fig. 8. Changes in multi-scale entropy of real signal detection system.

將策動力幅值r調節至0.825, 也即使系統處于臨界混沌狀態, 將真實水聲信號加入檢測系統,系統相軌跡圖由圖10(a)所示混沌狀態躍變至圖10(b)所示周期狀態, 成功實現對實測水聲信號中目標信號的檢測. 所以多尺度熵方法可以很準確地計算系統閾值.

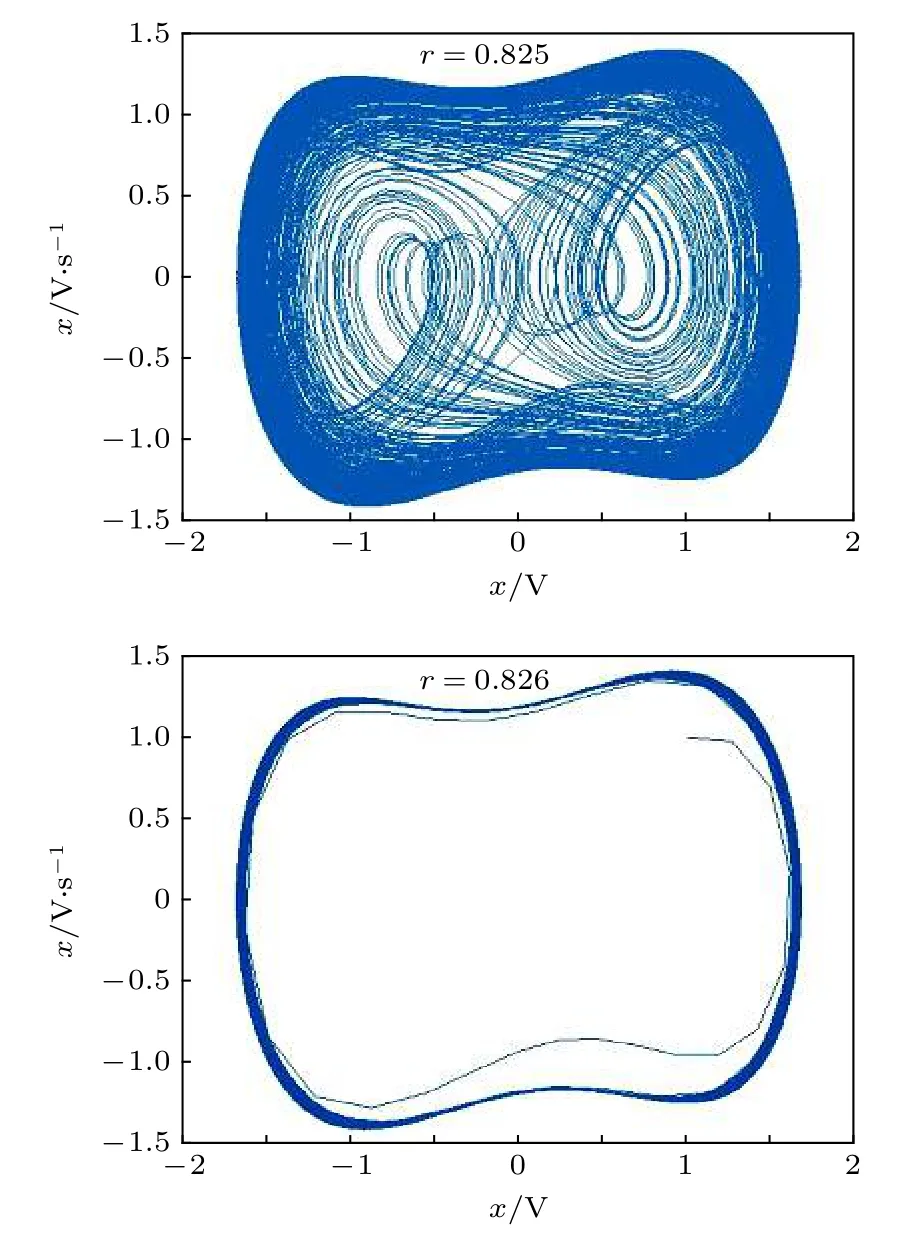
圖9 仿真實驗求解真實水聲信號檢測系統閾值Fig. 9. Simulation experiment to solve the threshold of real underwater acoustic signal detection system.

圖10 對真實水聲信號的檢測 (a) 系統未添加真實信號; (b)系統添加真實信號Fig. 10. Detecting real underwater acoustic signals: (a) The system did not add a real signal; (b) system adds real signal.

4 最大多尺度熵算法

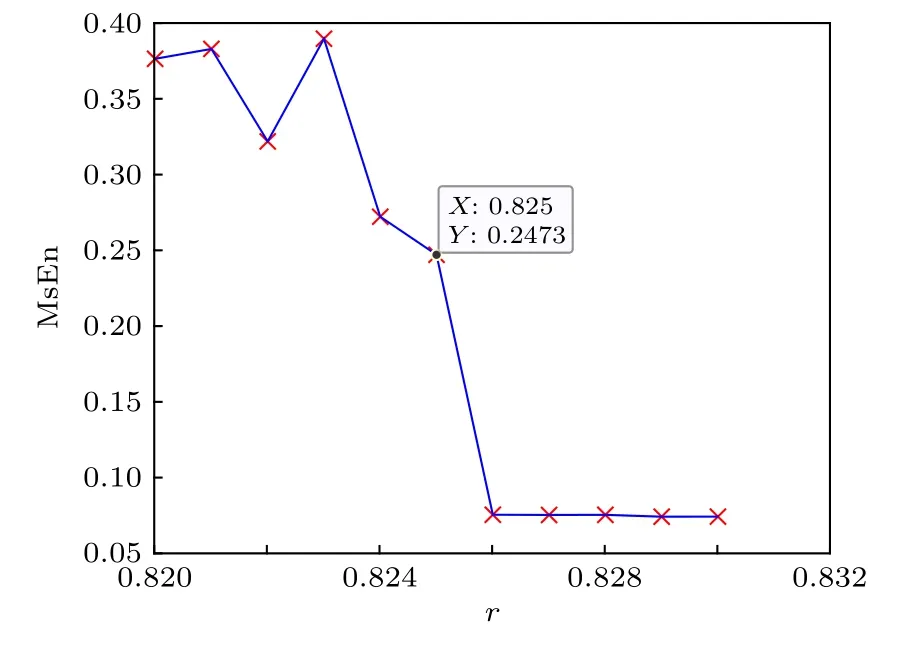
圖11 5rad/s 正弦信號檢測系統多尺度熵變化情況Fig. 11. Variation of multi-scale entropy in 5 rad/s sinusoidal signal detection system.

圖12 仿真實驗求解5 rad/s 正弦信號檢測系統躍變閾值Fig. 12. Simulation experiment to solve the threshold of 5 rad/s sinusoidal signal detection system.

利用系統(1)將頻率參數改為5 rad/s, 其他參數不變, 得到多尺度熵變化情況如圖11 所示,分析可知多尺度熵方法求得系統閾值為rd=0.825 .進行仿真實驗, 仿真結果如圖12 所示, 可知仿真實驗求得的系統閾值為rd=0.826 , 與多尺度熵方法求解結果有偏差, 說明多尺度熵方法存在一定問題.

我們分析是時間序列段的隨機選取造成了閾值計算的偏差, 第三部分中計算采用的時間序列是在整個Duffing 序列中隨機選取的長度為30000的子序列段, 在一般狀態下隨機選取的子序列段可以代表整個時間序列的復雜度, 但是當系統在接近或處于臨界混沌狀態時會有部分序列段已經處于周期狀態, 如圖13 所示, 該狀態下隨機選取的時間序列段不能代表整個時間序列的狀態.

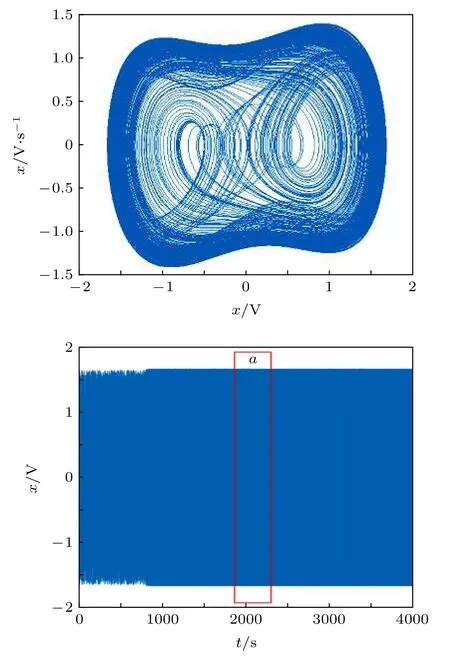
圖13 系統臨界混沌狀態Fig. 13. Critical chaotic state of the system.

圖13 表示系統正處于混沌狀態, 但右圖中a段序列為周期序列, 取用a序列進行多尺度熵計算會得到較小熵值, 誤認為系統已經進入周期狀態, 導致所求系統躍變閾值偏小, 這便是在前述計算中多尺度熵方法計算結果與仿真實驗計算結果存在偏差且偏小的原因. 針對這一現象考慮在整個序列中尋找復雜度最大的子序列及其對應的多尺度熵值, 用復雜度最大的子序列代表整個時間序列, 當系統復雜度最大的子序列對應的熵值處于較小值且趨于平穩時, 則系統必定已經進入周期狀態, 可更加精確計算系統閾值. 為此引入遺傳算法,利用遺傳算法尋找Duffing 序列最大多尺度熵.

4.1 遺傳算法

遺傳算法(genetic algorithm, GA)是基于生物的自然選擇和遺傳機理而形成的一種全局尋優算法, 其本質是一種基于概率的隨機搜索算法. 一般認為GA 的計算流程為[20]:

1) 問題解的遺傳表示;

2) 產生初始染色體;

3) 設計適應度函數, 根據適應值對個體進行優劣判斷;

4) 進行選擇操作, 選出適應值高的染色體, 使它們成為新一代種群中的染色體;

5) 對新種群進行交叉操作, 產生新的染色體;

6) 進行變異操作, 避免算法陷入局部最優解的情況;

7) 對新的種群重復進行選擇、交叉、和變異操作;

8) 經過給定次數的迭代或滿足給定的條件后,把最好的染色體作為優化問題的最優解.

4.2 最大多尺度熵算法步驟

基于遺傳算法的思想, 本文提出一種最大多尺度熵算法, 算法具體步驟為:

1) 利用Duffing 系統方程迭代產生一組時間序列X=[x1,x2,x3,··· ,xm] , 將X作為一個種群,時間序列的長度為m;

2) 將X分成l個染色體, 分別為CC=[C1,C2,C3,··· ,Cl] , 每個染色體的長度為n, 染色體的數目l=m/n.CC中前i個染色體構成的種群C=[C1,C2,C3,··· ,Ci] 作為算法的初始種群, 循環次數為N=l ?i;

3) 選取多尺度樣本熵作為適應度函數, 通過計算種群中每個染色體的多尺度樣本熵值來判斷各個染色體的優劣, 作為選擇的依據;

4) 對初始種群C=[C1,C2,C3,··· ,Ci] 進行適應度測試, 計算每個染色體的適應度值, 得到種群中每個染色體所對應的適應度值分別為M=[M1,M2,M3,··· ,Mi] ;

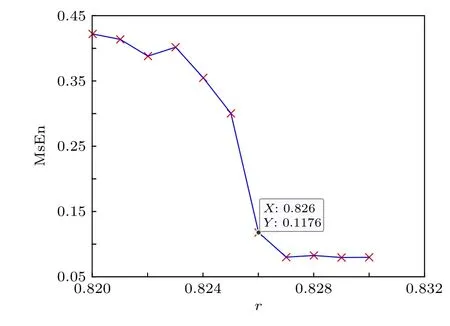
5) 按照得到的適應度值, 從大到小對染色體進行排序, 重新排序后得到的種群為對應的適應度值為. 對重新排序后的種群C′按照隨機數w(0

6) 得到由i個新的染色體組成的種群, 返回到步驟(4)進行循環迭代計算, 直到滿足循環條件;

7) 得到Duffing 時間序列中熵值最大的子序列及其對應的熵值.

4.2.1 最大多尺度熵算法有效性

第三部分5 rad/s 正弦信號檢測系統中, 策動力幅值r=0.826 , 系統處于混沌狀態, 多尺度熵方法求得MsEn = 0.0778, 利用最大多尺度熵算法計算r=0.826 時Duffing 序列最大多尺度熵值,取Duffing 序列長度為400000, 每個子序列長度為30000, 初始染色體個數為6, 交叉點為隨機數, 每次循環淘汰的染色體數目為1, 循環結束后得到6 個復雜度較大的子序列段, 其對應的熵值結果如表1 所列.

表1 Duffing 子序列段熵值( r=0.826 )Table 1. Entropy value of the Duffing subsequence segment ( r=0.826 ).

分析表1 可知, 程序經過遺傳進化找到了4 組熵值大于0.0778 的混沌子序列, 最大多尺度熵值為0.1188.r=0.827 時, 系統處于周期狀態, 多尺度熵方法求得MsEn=0.0754, 利用最大多尺度熵算法計算r=0.827 時Duffing 子序列熵值, 結果如表2 所列.

表2 Duffing 子序列段MsEn 值( r=0.827 )Table 2. Entropy value of the Duffing subsequence segment( r=0.827 ).

從表2 中看到, 經過遺傳進化找到了5 組大于0.0754 的子序列, 最大MsEn 為0.0822, 但因r= 0.827 時系統已經處于周期狀態, 所求結果與多尺度熵方法所求結果相差不大. 結合表1 和表2可以知道, 最大多尺度熵算法可以很有效地尋找到復雜度較大的子序列, 得到最大多尺度熵, 可更加精確地求解系統的躍變閾值.

針對5 rad/s 正弦信號檢測系統的偏差問題,現用最大多尺度熵方法求該系統閾值, 分析偏差是否仍舊存在. 取Duffing 序列長度為400000, 每個子序列長度為30000, 初始染色體數目為6, 交叉點為隨機數, 結果如圖14 所示, 分析可以確定系統躍變閾值為0.826, 與圖12 仿真實驗所求閾值0.826 相同, 所以最大多尺度熵方法可以很好地解決序列段的選取問題, 準確求解系統躍變閾值.

圖145 rad/s 正弦信號檢測系統最大多尺度熵變化情況Fig. 14. Variation of maximum multi-scale entropy of 5 rad/s sinusoidal signal detection system.

5 結 論

本文針對Duffing 系統躍變閾值難以確定這一問題進行了研究, 首次提出利用Duffing 系統周期態和混沌態多尺度熵值差異明顯這一現象, 通過分析多尺度熵與策動力幅值的關系對閾值進行求解, 對于該方法存在的問題, 結合遺傳算法進行了改進, 通過對正弦信號與方波信號檢測系統的閾值求解, 證明該方法可以快速準確得到系統躍變閾值, 解決了閾值難以快速準確得到的問題, 為混沌振子檢測低信噪比信號的實際應用奠定了很好的基礎.