基于共振Raman 增強的三階非線性過程*

裴麗婭

(北京化工大學數理學院, 北京 100029)

1 引 言

自電磁感應透明(electromagnetically induced transparency, EIT)被提出[1?3]以來, 由于其在原子共振頻率處光的吸收被減小甚至消除的特性, 人們認為利用EIT 可以增強四波混頻(four-wave mixing, FWM)等多波混頻的非線性過程[4?7]. 在均勻增寬系統中, 人們常以量子Fano 干涉解釋EIT 的物理. 而在多普勒增寬系統中, 我們提出[8?10]:EIT 是一個線性吸收被共振受激拉曼譜(stimulated Raman spectroscopy, SRS)修正的過程, 其透明窗口的出現來自于Raman 增益對線性吸收的補償. 在此觀點的基礎上, 本文將進一步全新闡述在多普勒增寬L-型能級系統中FWM,EIT 與SRS 三者之間的本質關系. 實際上,Raman 現象與FWM 總是存在很強的關聯.Jiang 等[11]提出了一種研究Raman 增強非簡并FWM 的相敏方法. 在熱銣蒸氣中, Zibrov 等[12]演示了光場對由微波場誘導和維持的原子基態塞曼相干作用從而產生受激Raman 散射引起的FWM 過程. 而Liu 等[13]則在基于Raman 驅動相干的高效FWM 過程中, 實現和研究了多Raman 增益共振. Carrasco-Sanz 等[14]報道了通過Raman 放大增強的級聯FWM 產生參考頻率梳的研究. 另一方面, Vanholsbeeck 等[15]給出了參量FWM 影響受激Raman 增益的完整實驗表征. Michaud 等[16]在冷原子中實現了Raman 增益與FWM 的干涉. 而Silva 等[17]則是從理論上分析了高雙折射光纖FWM 過程中受激Raman 散射的影響. 在前人的工作中, 也有與本文相關的研究. Romanov 等[18]通過在Rb85中實現Raman 吸收, 從而對Rb87中產生的基于EIT 的FWM 信號進行抑制. Parniak 等[19]通過基態原子相干得到了Raman 散射與FWM 信號的強關聯. 利用雙L-型能級系統, Lee 等[20]實現了基于EIT 的共振FWM 的高轉換效率. 利用L-型EIT 系統進行光存儲[21,22]是近年來的重要研究方向, 而光信息的一次完整寫入和讀出可以看做是一個FWM 過程.

承接前期的工作[8], 我們來看一下建立Raman 增益的過程. 對于L-型三能級系統, 當兩束入射光場(探測光和耦合光)頻率差等于 ωR(原子兩基態能級之間的Raman 共振頻率)時, 在系統中首先形成兩基態之間的Raman 相干; 當此原子相干進一步與耦合光相互作用時, 就會在?1=?2處散射出anti-Stoke 光子, 這便是窄線寬Raman 增益.

Raman 散射最終如何呈現在光譜中, 取決于探測方式. 前期我們利用鎖相放大器對典型EIT 系統進行調制解調, 期望濾除弱探測光的多普勒展寬吸收背景, 得到純粹的窄線寬Raman 增益信號峰, 但由耦合光帶來的泵浦效應所形成的的吸收背景卻無法消除[9]. 為了將上述Raman 增益信號峰與泵浦吸收背底也能進行分離, 本文設計了一個非線性過程: 首先, 介質系統在探測光和耦合光這兩束光作用下形成Raman 相干, 但與其進一步作用的是線偏振方向偏轉90o之后的耦合光, 為了區分稱其為控制光. 最終, 得到與探測光偏振分離的Raman 增益, 其經過介質之后相應的新光場即為FWM 信號. 我們將看到, 在多普勒增寬L-型能級系統中的FWM 過程被增強, 在本質上是由于Raman 共振得到滿足而非量子干涉. 同時, 我們提出: FWM 與EIT 作為兩種完全不同的非線性效應, 在本質上均來源于受激Raman 散射, 區別在于探測方式和對象的不同, 使其成為了完全不同的兩種光譜. 由于在多普勒增寬系統中原子速度呈高斯形式分布, 單個原子的量子特性被淡化; 在一定條件下, 不同速度原子群之間宏觀極化干涉成為了影響FWM 光譜的主要因素.

2 理 論

考慮如圖1 所示的原子能級系統. 與之相互作用的耦合光場和控制光場, 分別記為E2=ε2e?i(ω2·t?k2·r)(作 用 于 態與之 間)和E3=ε3e?i(ω3·t?k3·r)(作用于態之 間). 這里, 與不同線偏振方向的耦合光(‖)和控制光(⊥)分別相互作用的, 是兩個不同的簡并激發態能級, 分別記作和以便區分. 另外, 探測光場(‖)記為E1=ε1e?i(ω1·t?k1·r)(作用于態與或之間). 系統的原子躍遷頻率記為?1(i=1,2,3 ),與相應激光場頻率的失諧可以記為?i=?i ?ωi(i=1,2,3 ). 圖1 中, 原 子 兩基 態能 級 之間 的Raman 共振頻率記為ωR.

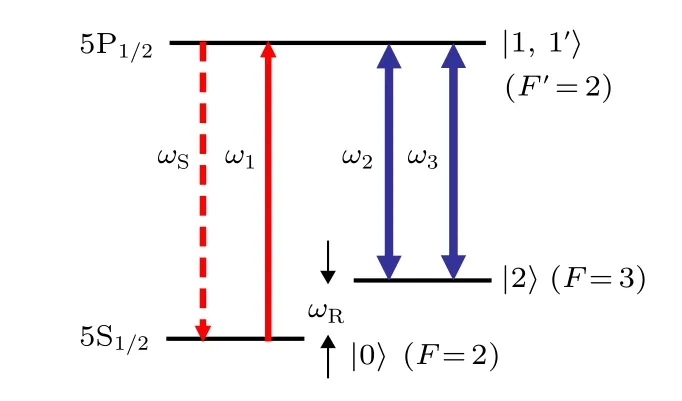
圖1 85Rb 原子D1 線能級系統Fig. 1. D1 line energy-level diagram of 85Rb.

通過求解密度矩陣方程, 在弱探測光以及ρ00≈1,ρ22≈0 近似條件下, 得到與SRS 相關的三階密度矩陣元, 其相應的極化強度如下:

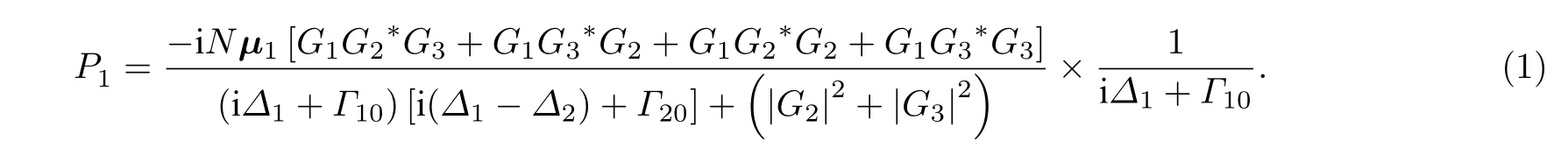
這里,Gi=μiEi/?(i=1,2,3 )為光場與原子相互作用的耦合系數, 記μi為相應能級態之間的偶極矩陣元; 取近似Γ21≈Γ10, 用Γ10和Γ20分別表示激發態與基態、以及兩基態之間的橫向弛豫率.

如圖1 所示, 我們關注的是三個激光場(ω1,ω2,ω3)與原子介質相互作用產生的三階非線性過程; 若其中兩個入射場的頻率滿足ωR=ω1?ω2時,在頻率ωs處散射的信號就會被Raman 共振增強.(1)式表示, 在兩束光(ω2,ω3)耦合下的弱光(ω1)探測系統, 包含了四個實質上的三階非線性路徑:

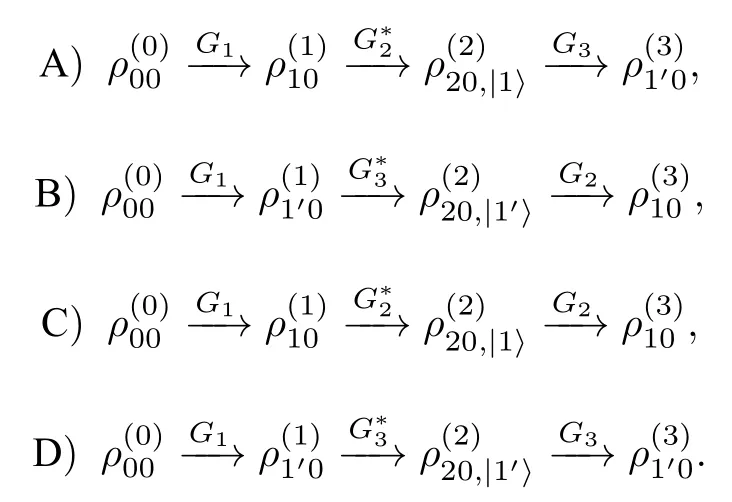
當取ω2=ω3時, 相應于以上四個路徑產生的受激Raman散射光子的頻率: A)ωs=ω1?ω2+ω3, B)ωs=ω1?ω3+ω2, C)ωs=ω1?ω2+ω2和D)ωs=ω1?ω3+ω3, 均為ωs=ω1. 同時, 前兩個路徑A 和B產生的散射光子與探測光的偏振方向相互垂直[23],從而可以利用偏振分束器進行空間分離, 得到的是無背景的窄線寬FWM 信號. 然而, 后兩個路徑C 和D 產生的散射光子, 因與探測光的偏振方向相同從而無法分離; 將上面的(1)式與文獻[8]中(10)式

進行對比, 可以看到: 此處Raman 散射光子對探測光經過介質的線性吸收(形成多普勒展寬和泵浦吸收背底[9])進行補償, 從而在探測光吸收譜的?1=?2處(Raman 共振增強)看到一個窄線寬的吸收減少, 亦即前人觀察到的EIT 現象[24].

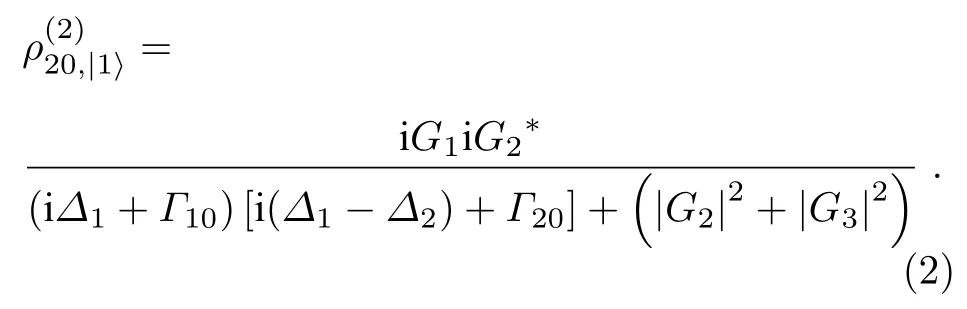
從(1)式可以得到與該路徑相應的三階非線性原子極化(用極點形式表示):

其中

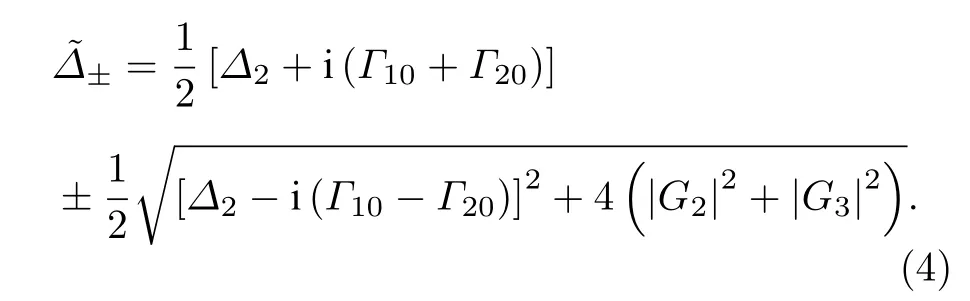
通過(3)式的三個極點, 來看看基于Raman 相干的三階非線性過程. 首先從(2)式看出, 兩光場(探測光和耦合光)與原子介質相互作用會誘導產生基態與之間的原子Raman 相干ρ20; 當形成的原子相干進一步與控制光相互作用時, 就會在單光子共振(?1=0, 即極點?1=iΓ10的實部)處放出受激Raman 散射光子, 也就是(1)式的第一部分(即路徑A)所表達的三階非線性過程. 而在建立原子相干ρ20的過程中形成的綴飾態, 亦會對?1=?±(即極點的實部)處的受激Raman 散射光子產生吸收. 根據(4)式, 當耦合光共振(?2=0 )時, 系統的綴飾態位于處. 經原子系統產生的FWM 信號, 其線寬與系統的吸收系數和色散系數均有關系.

3 實 驗

如圖1 所示, 作用于85Rb 原子D1 線 5S1/2,F=3→5P1/2, F′=2 之間的是線偏振相互垂直的耦合光場w2(‖)和控制光場w3(⊥), 需注意的是:在如圖2 所示的實驗裝置中, 這兩個光場來自同一臺795 nm 半導體激光器DL2, 其頻率相等(ω2=ω3). 作用 于 5S1/2, F=2→5P1/2, F′=2 之間 的是水平偏振(‖)的弱探測光場ω1, 該光場來自另一臺單獨的795 nm 半導體激光器DL1. 三束光經過一個偏振分束器合成一路后近似同向傳播: 其中耦合光與控制光完全重合, 與探測光在Rb 泡(長度75 mm; 室溫27 ℃)中心處光斑重合然后以極小的角度分開; 三束光的光斑高斯直徑均約為1.5 mm, 其均經過光纖以改良光斑質量. 在這里,介質的多普勒展寬線寬大約為510 MHz. 我們在與探測光線偏振相互垂直的方向上檢測到了窄線寬信號光(ωs); 并且若擋住耦合光或控制光時, 信號光均會消失. 實驗過程中, 在介質之前利用斬波器對激光器DL2 發出的光進行強度調制. 然后, 將經過Rb 介質之后的探測光和產生的FWM 信號光分別接到鎖相放大器進行解調, 得到了高信噪比的探測光(ω1)吸收譜(多普勒展寬背底被濾除)和FWM(ωs)光譜.

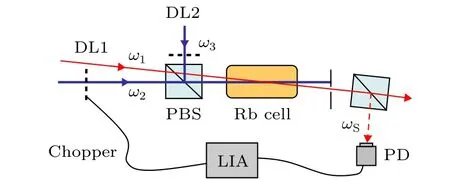
圖2 實驗裝置簡圖. 其中, DL1 和DL2: 半導體激光器;Chopper:斬 波 器; PBS:偏 振 分 束 器; PD:光 電 探 測 器;LIA: 鎖相放大器Fig. 2. Experimental setup. DL1 and DL2, diode lasers;PBS, polarizing beam splitter; PD, photodetector; LIA,lock-in amplifier.

我們分別將耦合光鎖在85Rb 的 5S1/2,F=3→5P1/2,F′=2原子躍遷線上, 即取?2=0 , 以及正失諧350 MHz 的頻率處, 即取?2=350 MHz ;掃描探測光頻率, 并始終保持其光強較弱I1=0.10 mW.圖3(a)和圖3(b)給出了兩種耦合光失諧大小的情況下, 測得弱探測光吸收譜(I1), 和另一個偏振方向上的FWM 信號(IS). 可以觀察到一個共同的特征: 窄線寬FWM 信號出現的位置(?1=?2), 也是探測光透明窗口出現的位置. 同時, 與在耦合光共振條件下不同的是: 在耦合光失諧時, 探測光有一個從窄線寬的吸收減少(透明窗口)到吸收增強的過渡[10]. 根據上面的理論我們知道, 這是測量手段的不同導致的: FWM 信號是非線性介質系統產生的新光場, 只有Raman 正增益可以被檢測到; 因在建立Raman 相干過程中產生的綴飾態而引起的Raman 損耗, 最多只能消耗相應頻率處的散射光子, 而不能讓信號強度為負值.當然, 信號從產生到穿出介質其譜線必然受介質的色散修正.

圖3 (a) 耦合光共振( ?2 =0)和(b) 耦合光失諧( ?2 =350 MHz )下的弱探測光吸收譜(黑色實線)和窄線寬FWM 信號(紅 色 實 線). (注 意: 實驗中失 諧 條 件下的信 號較小, 這里為了看圖清楚, 圖(b)的光譜強度相應地均增大到實際強度的2.5 倍)Fig. 3. Experimental results for the transmission intensity of the weak probe beam (black solid line) and the FWM signal with narrow linewidth (red solid line) as a function of D1: (a) D2 = 0; (b) D2 = 350 MHz. (Note that in order to see the details clearly, the spectral intensity in Fig. (b) is the result of magnification to 2.5 times the actual situation.).

從圖3 可以看出, 除了探測光掃描到共振附近的窄線寬凸起峰, 在其它頻率失諧處, FWM 光譜強度基本是零. 檢測到的是優良信噪比的FWM 信號. 可以想到, 如果不在探測之前放置偏振分束器,將得到: 四個路徑產生的窄線寬SRS 不會空間分離, 其均對探測光泵浦吸收進行補償, 讓探測光吸收譜呈現出窄線寬透明窗口.

4 理論模擬與討論

在前面的理論中, 研究了在均勻增寬系統中的Raman 共振增強FWM. 而對于實驗, 還要考慮介質的多普勒效應, 需將前面的失諧量分別替換如下:

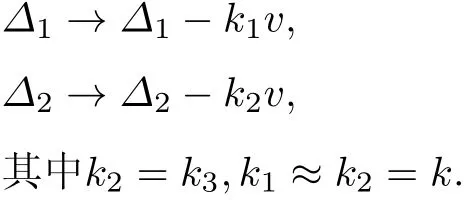
之后, 將多原子系統對速度積分, 速度在一個方向上的分布W(v) 取高斯形式. 與FWM 信號對應的系統非線性極化給出如下:

最終信號強度(IS)正比于.并且,(5)式中的三階非線性極化P1(A+B)(v) 可以被表達如下:

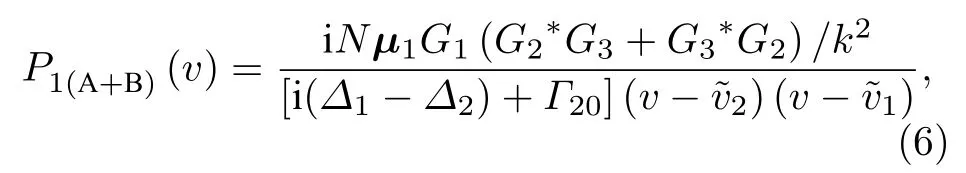
其中:

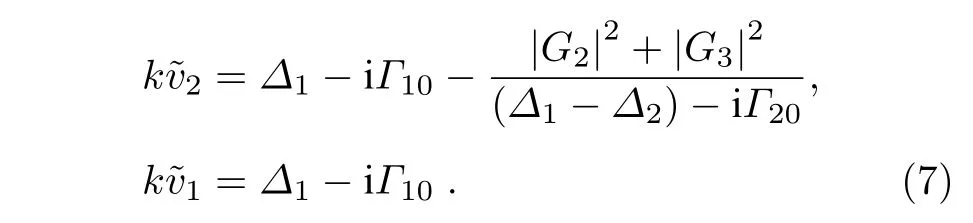
如圖4 所示, 任意選取了耦合光共振(?2=0 )的情況進行了理論擬合(黑色-實線). 從圖4 可以看出, 除了實驗信號(紅色-星星)有強度較弱且穩定的雜散光噪聲背景之外, 在 ?1=?2處出現的窄線寬FWM 信號與理論擬合符合得非常地好.

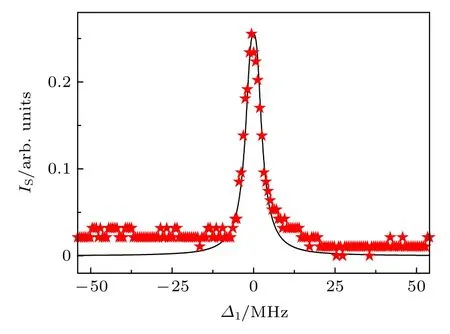
圖4 掃 描 弱 探 測 光 頻 率 時, FWM 實 驗 信 號(紅 色-星星)和理論擬合(黑色-實線). 實驗采用的耦合光強度I2 =1.97 mW, 控制光強度I3 = 7.4 mW; 理論模擬采用的參數是: Γ10 =7.2 MHz , Γ20 =0.72 MHz, G2 =10.8 MHz ,G3 =20.4 MHz )Fig. 4. Experimental results (red star) and theoretical fitting (black solid line) for the FWM signal. The coupling field intensity I2 = 1.97 mW and the control field intensity I3 = 7.4 mW are used in the experiment. The parameters used in the theoretical simulation are Γ10 =7.2 MHz ,Γ20 =0.72 MHz , G2 =10.8 MHz , G3 =20.4 MHz .

從上述理論可以看出, FWM 信號的線寬與多普勒展寬(對應于實驗溫度)和耦合光(或控制光)強度有關. 圖5(a)和圖6(a)模擬了耦合光共振( ?2=0 )條件下的FWM 光譜(實線)和SRS光譜(虛線), 在圖5(a)中 ku/γ =50.7, G2/γ =0.5(黑線), 2.5(紅線), 4.0(藍線); 在圖6(a)中 G2/γ =4.0, ku/γ =50.7 (黑線), 101.4(紅線), 202.8(藍線).其中, g 為激發態與基態之間的縱向弛豫率. 從圖5(a)和圖6(a)可以看出, 隨著耦合光強度(I2)增大或多普勒展寬線寬(ku)減小, FWM 光譜線寬會相對變寬. 同時, 由于FWM 光譜經過了色散的修正, 其相對SRS 光譜來說線寬略寬. 但當耦合光強度越小或多普勒展寬線寬越大時, 兩種譜線線寬越趨于基本一致, 這是由于此種條件下: 在?1=?2=0 處, 色散變化越陡峭[24], 其對受激Raman 散射光穿出介質的線寬修正影響越小.

在一定條件下, 我們可以利用原子共振速度對FWM 譜線線寬進行解釋. 當取 ?2=0 時, 共振速度 v1和 v2對探測光頻率的依賴特性, 如圖5(b)和圖6(b)所示.當 ?1=0時(即在 ω1?ω2=ωR處), |v2/u|→∞ , 即在多普勒展寬線寬內只存在共振速度 v1, 具有該速度的原子群發射基于Raman共振增強的散射光子, 從而在 ?1=?2處出現信號峰, 如圖5(a)和圖6(a)所示(實線). 當 ?1遠離?1=?2, 即探測光遠離共振時, 得到 v1?v2?0 ,而這兩個速度的原子群分別貢獻散射光子和損耗散射光子, 從而相互抵消使得信號趨于零. 而在 ?1偏離 ?1=?2的過程中, 當 v2?u時, 共振速度 v2的原子群便可以有效消耗共振速度 v1的原子群貢獻的散射光子, 此時探測光頻率掃描到 ?1=(|G2|2+|G3|2)/ku ; 從圖5(b)和圖6(b)(實線)亦可看出, 當耦合光強度( |G2|2)減小或多普勒展寬( ku)增寬時, 探測光掃描到較小失諧 ?1處, 共振速度 v2就能有效地消耗受激Raman 散射光子讓信號迅速衰減, 從而使得最終的信號線寬較窄. 這就解釋了圖5(a)和圖6(a)中呈現的FWM 信號線寬的特點. 從上述分析可以看出, 與綴飾態共振的速度 v2, 起到了對共振速度 v1貢獻的Raman 增益線寬進行壓窄的作用, 并且FWM 光譜線寬

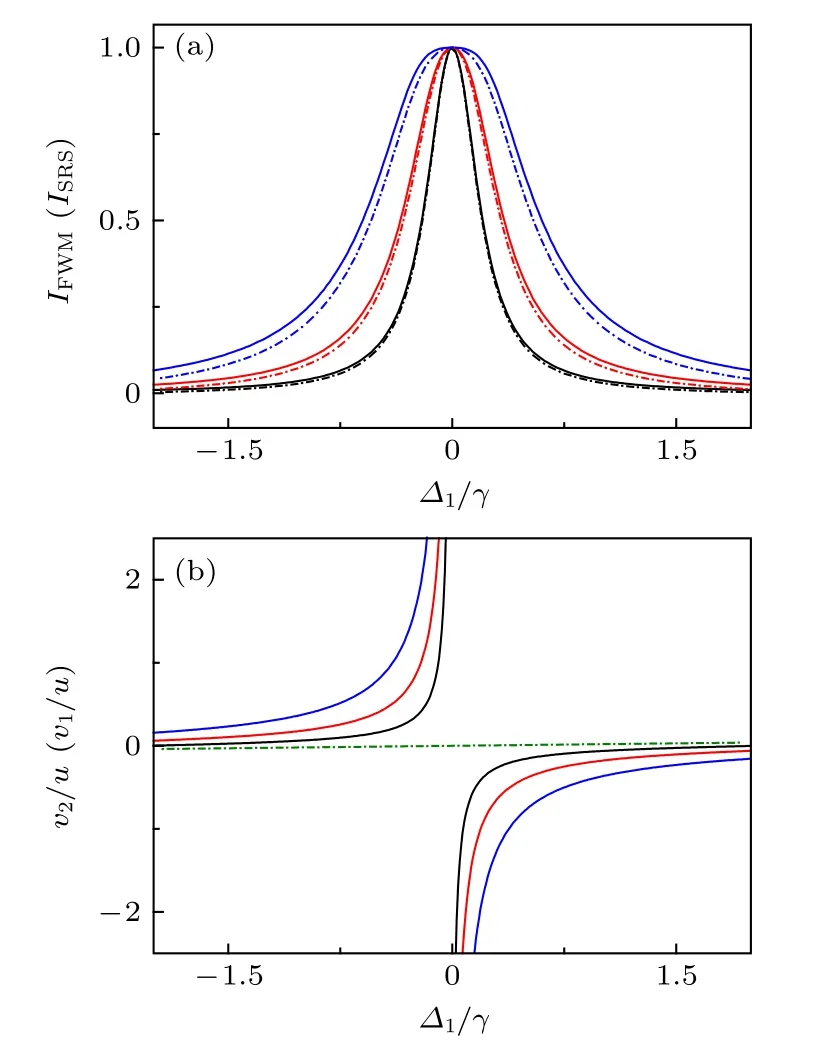
圖5 變化耦 合光強 度(I2)條 件下的(a)FWM 光譜(實線)和SRS 光譜(虛線), 和(b)原子共振速度 v2/u (實線)和 v1/u(虛線). 所取理論參數為: G2/γ =0.5 (黑線),2.5(紅線), 4.0(藍線)Fig. 5. (a) FWM (solid line) and SRS (dotted line), and(b) corresponding resonant velocities v2/u (solid line) and v1/u(dotted line) as a function of ?1/γ when G2/γ =0.5 (black), 2.5(red), 4.0(blue).

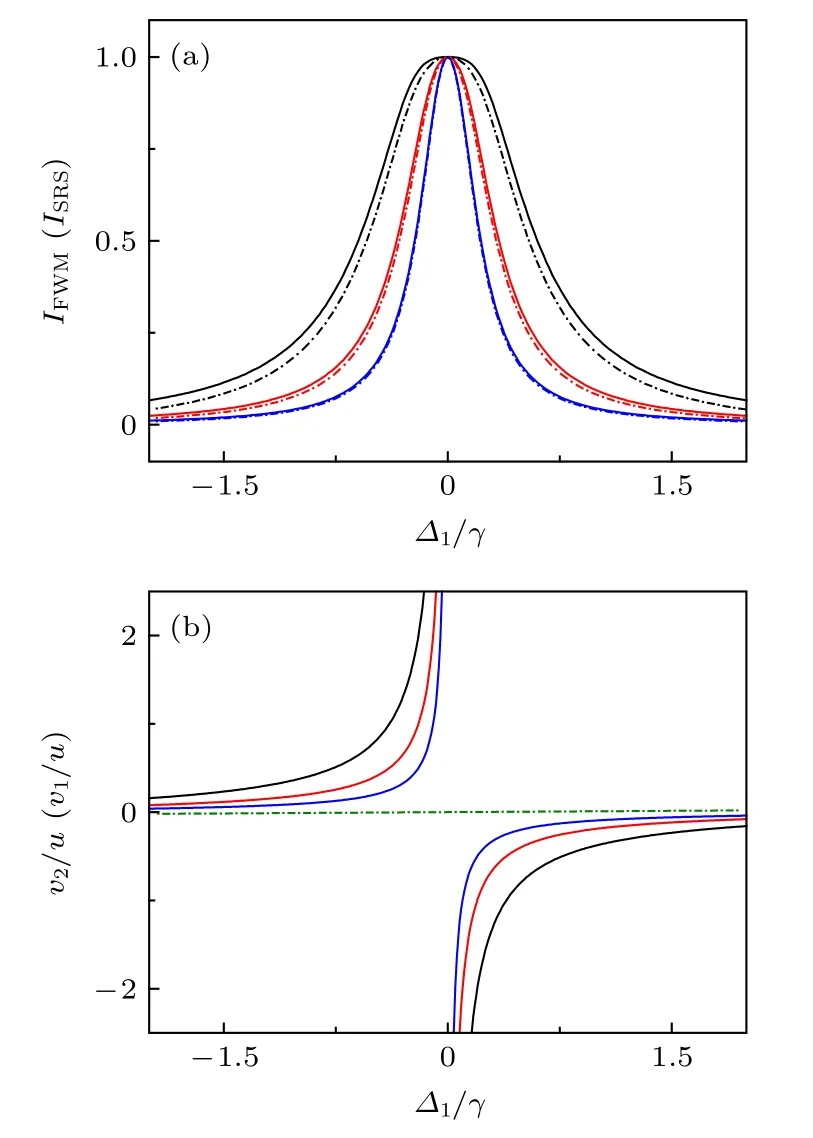
圖6 變化多普勒展寬線寬(ku)條件下的(a) FWM 光譜(實線)和SRS 光譜(虛線), 和(b) 原子共振速度 v2/u (實線)和 v1/u(虛線). 所取理論參數為: ku/γ =50.7 (黑線),101.4(紅線), 202.8(藍線)Fig. 6. (a) FWM (solid line) and SRS (dotted line), and(b) corresponding resonant velocities v2/u (solid line) and v1/u(dotted line) as a function of ?1/γwhen ku/γ =50.7 (black), 101.4(red), 202.8(blue).

5 結 論

本文承接前期的工作, 基于對EIT 現象提出的新詮釋, 進一步闡明了在多普勒增寬L-型能級系統中EIT 和SRS 以及FWM 三者之間的關系:共振EIT 吸收光譜的透明窗口, 本質上是基于三階非線性過程產生的Raman 增益對介質線性吸收修正之后的呈現; 而FWM 信號之所以被增強, 并不是因為前人提出的EIT 的本質---量子干涉, 而是因為相干Raman 共振得到了滿足. 在本質上,L-型能級系統中的FWM 信號與EIT 透明窗口均是基于受激Raman 過程, 區別僅在于探測手段的不同. 通過理論模擬得到, 在耦合光強度相對較小或多普勒展寬較大時, 介質色散對FWM 信號線寬的修正可以忽略, 就可以用不同速度原子群之間的宏觀極化干涉, 來解釋基于非線性過程最終的光譜呈現. 在耦合光共振(?2=0 )條件下, 與綴飾態共振的速度v2, 由于在偏離單光子共振的過程中越來越有效的起到消耗光子的作用, 從而對共振速度v1在以?1=0 為中心的頻率處貢獻的Raman 增益的線寬進行壓窄, 使得在雙光子共振?1=?2處看到窄線寬的凸起峰---FWM 信號. 并且, 耦合光強度相對越小或多普勒展寬越大時, FWM 信號的線寬越窄.