改進小波閾值對熱泵電機振動信號的去噪研究

王 盟， 余 粟， 馮益林

（1 上海工程技術大學 電子電氣工程學院， 上海201620； 2 上海工程技術大學 工程實訓中心， 上海201620）

0 引 言

熱泵電機是熱泵機組工作的核心部件，其運行狀態直接決定熱泵機組的工作質量。 所以熱泵電機的振動信號獲取與分析是保證穩定運行的重要環節。 由于其位于熱泵機組的內部，而且工作環境較為惡劣，使得監控過程中獲取的信號包含了噪聲干擾，呈現出非平穩時變特點。

小波閾值降噪方法能夠在減少誤差的同時保留更多有用的信號，被廣泛應用于非平穩時變系統。在傳統的小波閾值函數中：硬閾值函數降噪一般會產生相對較小的均方根誤差，但具有不連續性，處理信號時會產生跳變。 軟閾值函數整體連續，處理之后的信號較為平滑，但在重構信號時會產生恒定偏差，造成原信號過度失真。 文獻［5］中提出了含有e指數的新閾值函數，但不含調節因子，不能實現靈活去噪。 文獻［6］中提出含有調節因子a、b 的改進閾值函數，可以靈活調節適應含噪信號，但計算量較大，數據處理較為困難。 另外，在實際信號處理過程中，隨著分解尺度的增加，要求噪聲引起的小波系數逐漸降低［2］，如果選擇固定閾值，就會導致信號失真嚴重。 對此，文獻［7－8］中提出了多尺度閾值去噪方法，具有較大的參考價值。

本文針對軟、硬閾值存在的不足，與多尺度的閾值相結合，提出了一種改進的新閾值函數。 新閾值函數引入了可調因子m 和n，不僅解決了傳統閾值函數存在的不連續性和恒等差問題，而且使得計算量相對減少。 將此閾值函數應用于熱泵電機信號的降噪處理中，在保留更多特征信息的基礎上，取得了較好的濾噪效果。

1 小波閾值去噪原理及計算

1.1 小波閾值去噪原理

小波閾值去噪的原理是先設定一個閾值λ， 假如小波系數小于λ，就把這個系數認定為噪聲產生的，將之消除；反之小波系數大于λ，就把該系數認定為信號產生的，將之保留。 最后采取小波逆變換對小波系數進行重構，得到去噪后的信號。 假設含噪的電機振動信號滿足f（t）＝f＾（t） ＋ω（t）。 其 中，f（t） 為原始標準信號，ω（t） 為噪聲信號。 小波閾值降噪步驟如圖1 所示。

圖1 小波閾值降噪流程Fig.1 Wavelet threshold noise reduction process

1.2 常見的閾值和閾值函數

閾值和閾值函數的選取直接決定信號去噪的效率。 目前常見的閾值選擇方法有：極值閾值估計、無偏似然估計、固定閾值估計以及啟發式估計等［10］。前2 種方法可以將少量分布在高頻部分的微弱信號提取出來，但是降噪效果卻相對較低。 而后2 種方法降噪效果較高，卻易于把有用信號當做噪聲消除。一般情況下多選擇固定閾值估計方法。

常用的閾值函數有軟閾值和硬閾值函數。 其定義如下：

軟閾值函數定義：硬閾值函數定義：

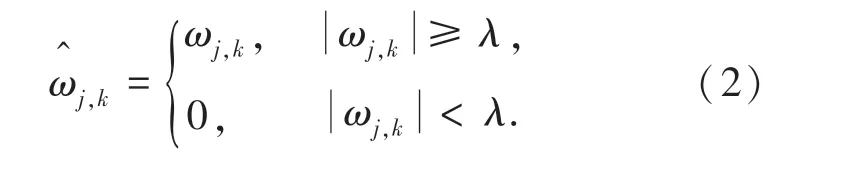
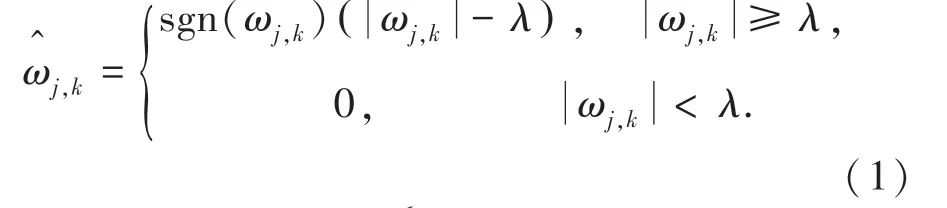
由公式可知硬閾值函數在閾值λ 處不連續，導致較大的均方誤差和波形震蕩，不具有原始信號的平滑性。 軟閾值函數是連續的，但處理前后存在固定的偏差，在產生較大誤差的同時也會造成部分有用信息的丟失。

2 改進閾值函數

2.1 一種新的閾值函數

為克服傳統閾值函數存在的恒等差和不連續問題，文獻［5］在軟、硬閾值折中函數的基礎上進行改進，提出了一種新的小波閾值函數：

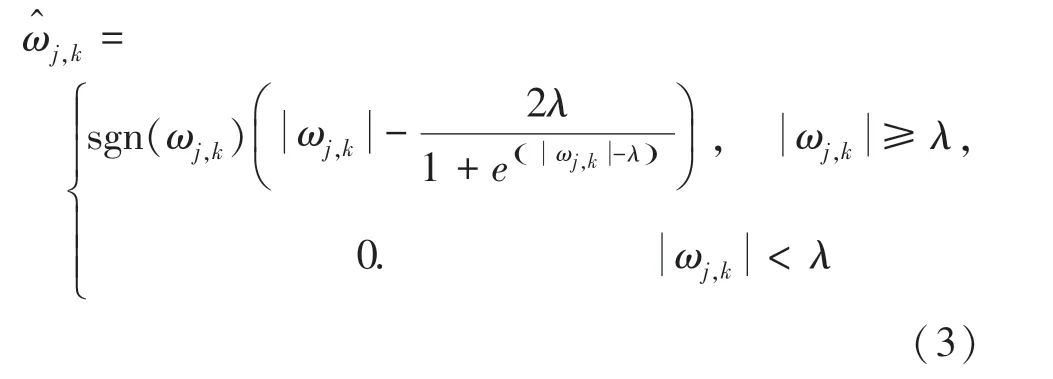
此式解決了恒等差和不連續的問題，卻不含調節因子，因此不能動態調整。 為此本文提出引入調節因子m 和n，得到新公式：

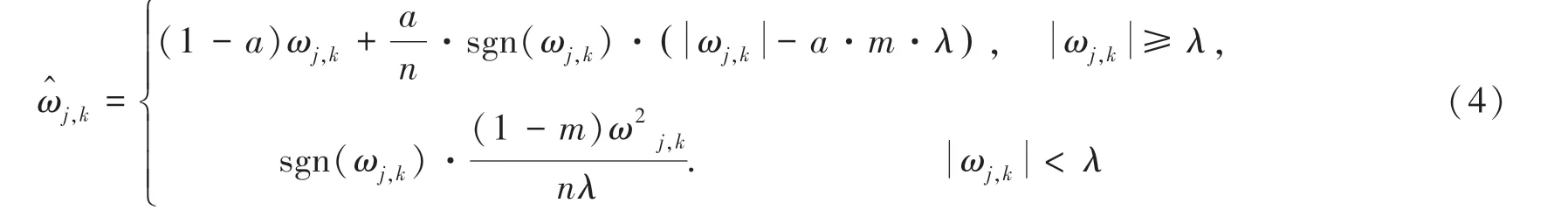
其中， a ＝e－n（1－m）（｜wj，k｜－λ）； 可調因子m ∈［0，1］； n 取正數。

新閾值的特征如下：

（1）改進的閾值函數具有連續性。

當λ ｜ωj，k｜→λ＋時：

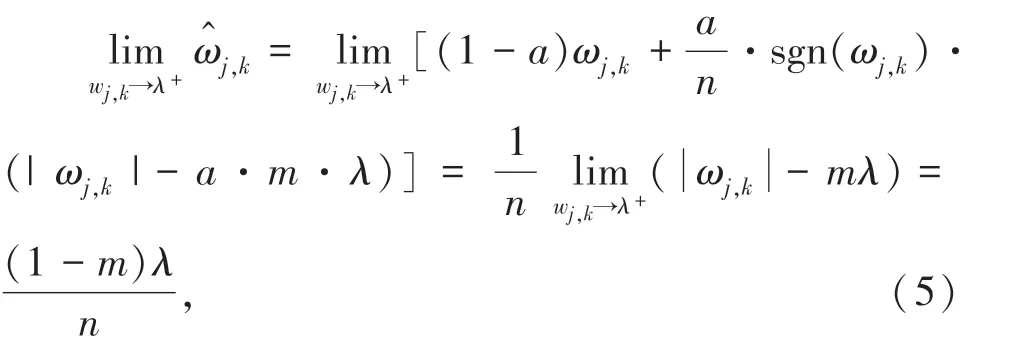
當｜ωj，k｜→λ－時：

即證明，新的閾值函數在λ 處連續。

（2）改進的閾值函數具有漸進性。 驗證如下：

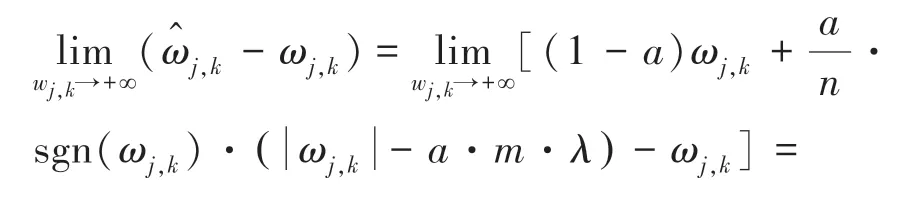
（3）改進的閾值函數偏差性較小。 驗證如下：

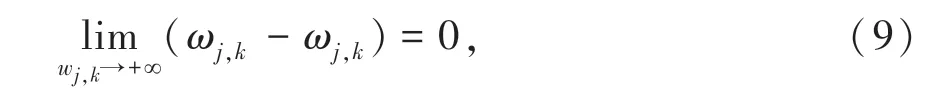
同理，

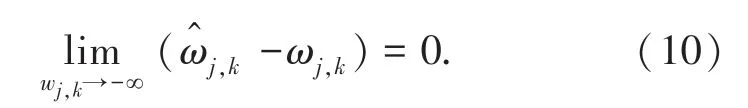
上式證明，隨著小波系數的增大，二者之間的差距會逐漸減小，解決了軟閾值的固有缺陷。

改進的閾值函數與軟硬閾值函數對比如圖2 所示，由圖可知新閾值函數既解決了軟閾值函數恒等差問題，也克服了硬閾值函數在λ 處不連續的缺點。

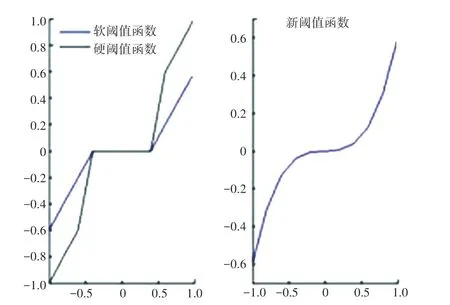
圖2 新閾值函數與軟硬閾值函數對比Fig.2 Comparison of the new threshold function and the soft and hard threshold function

2.2 可調因子的取值分析

令m ＝1，n ＝1，新閾值函數可演變為軟閾值函數；令n →∞，則其可變為硬閾值函數。 這證明新閾值函數具有可調性，通過改變m 和n 的取值以適應實際信號噪聲變化［4］，最終實現優化的目標。 通過多組實驗計算對比，對小于60 dB 的噪聲去噪，當m＝0.83，n ＝6 時，可以取得最佳的降噪效果；對大于60 dB 的噪聲去噪，當m ＝0.89，n ＝7 時，可以取得最佳的降噪效果。

2.3 確定最優閾值

傳統小波閾值一般采用固定值，而實際降噪時小波系數與分解尺度成反比。 即分解尺度增大，小波系數隨之變小。 為適應此規律，以達到保留更多有用信號的目的，要求應選取多尺度小波閾值。 為節省計算時間，本文采用文獻［7］中的小波閾值選取方法。 張振鳳在文獻［7］中基于lipschitz 指數論證了第j ＋1層小波系數約為第j 層的倍，提出了：

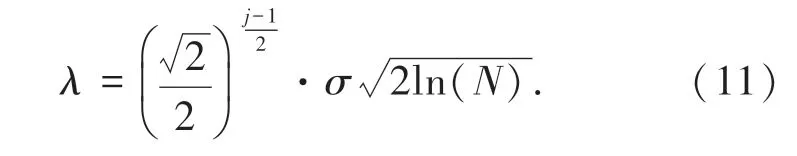
3 實驗仿真

為驗證改進算法的效果，首先設置原始含噪信號為x（t） ＝10sin（0.32t） ＋noise（t） ，其中t 屬于［0，500］，noise（t） 為Gauss 噪聲。 分別采用軟閾值函數、硬閾值函數、文獻［5］中的閾值函數和改進的新閾值函數對加噪信號進行降噪處理，降噪效果如圖3 所示。 其中圖3（a）為結合固定閾值的實驗效果，圖3（b）為結合多尺度閾值的實驗效果。 由圖3可以看出改進后的新閾值函數降噪信號，即圖3（b）中（f）的波形最接近原始信號波形，其信噪比為18.37，相比于其它幾種降噪方法，信噪比約提高了7%～15%，由此驗證了改進算法具有較高實效性。

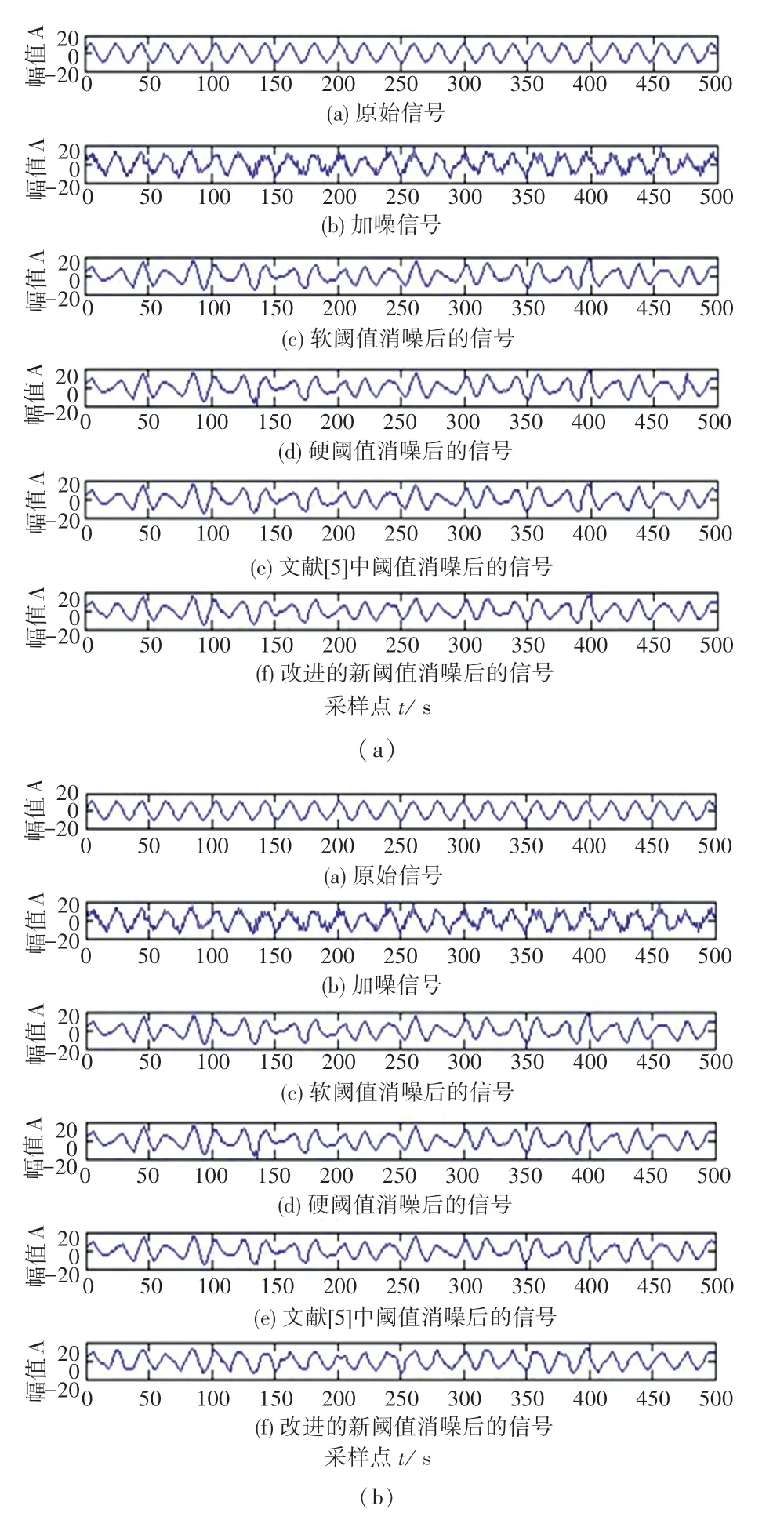
圖3 對加噪的正弦信號降噪處理實驗效果Fig.3 Experimental effect of noise reduction processing on sine signal with noise added

以山東長清工業園區某辦公樓的地源熱泵機組集成監控系統中的電機軸承振動信號為例。 熱泵電機的轉速為3 000 r／min，采樣頻率為f1＝20 KHz。待熱泵機組平穩運行后，通過加速度傳感器對電機軸承采集800 個采樣點。 由于采集的熱泵電機軸承振動信號較弱，添加50 dB 高斯噪聲以貼近真實情況。 對熱泵電機振動信號采用sym5 小波基函數，進行4 層小波分解。

為證實結合多尺度閾值改進的新閾值函數在熱泵電機振動信號降噪中的高效性，采用各閾值函數分別結合固定閾值和多尺度閾值對采集的電機軸承振動信號進行降噪處理仿真。 各閾值函數結合固定閾值降噪效果如圖4 所示，各閾值函數結合多尺度閾值降噪效果如圖5 所示。

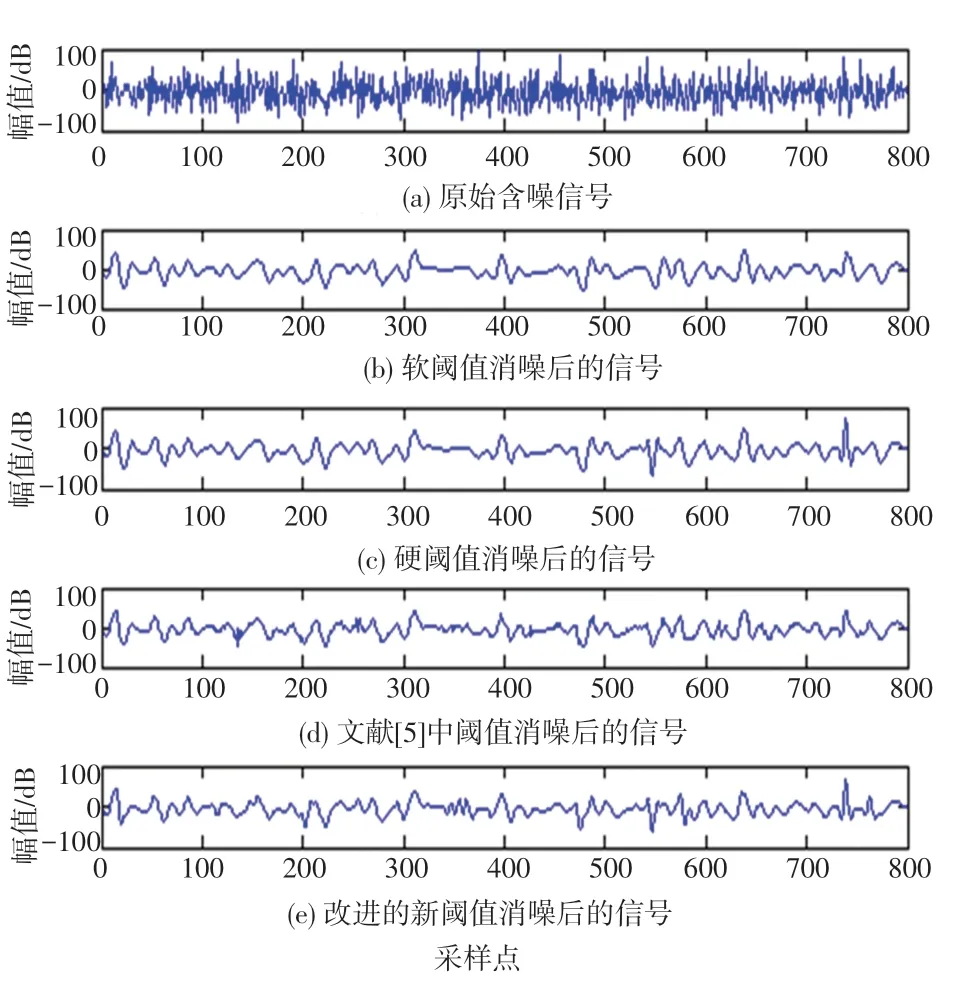
圖4 結合固定閾值降噪效果Fig.4 Noise reduction effect combined with fixed threshold

將改進的新閾值函數降噪信號與原始含噪信號在頻域上展開對比，如圖6 所示。 可以看出新閾值函數在頻域上能很好地保留尖峰值和突變部分，并可將噪聲引起的干擾有效地降噪處理，提高信噪比，還原度較高。

為了讓去噪效果表現的更直觀，此處引入數據分析的方法。 將獲取的原始信號作為標準信號f（t），經過降噪處理之后的預估信號為， 則信噪比定義如下：

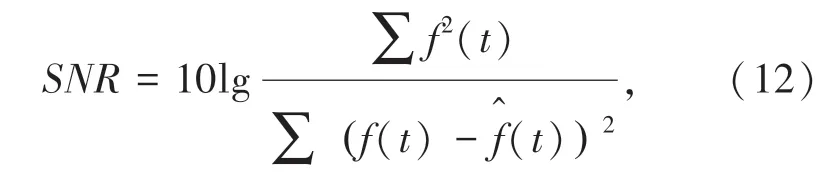
原始信號和預估信號之間的均方根誤差為：

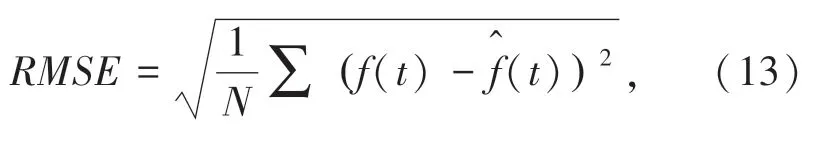
圖5 結合多尺度閾值降噪效果Fig.5 Noise reduction effect combined with multi－scale threshold

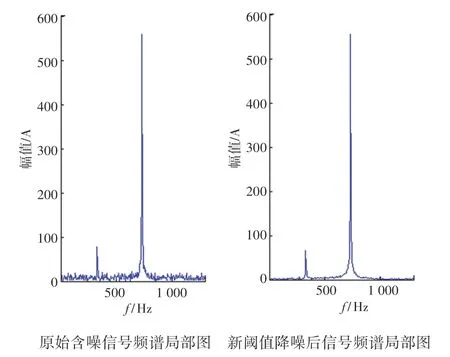
圖6 原始含噪信號和降噪信號頻譜圖對比Fig.6 Comparison of the spectrum of the original noise－containing signal and the noise－reduced signal

在降噪過程中，為衡量降噪信號的還原程度，定義維持率：

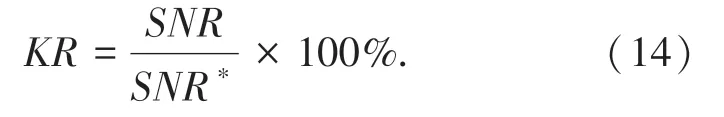
其中，SNR 為降噪后信號的信噪比， SNR?為原始信號的信噪比。KR 越大表示還原效果越好。

由式（12）、（13）、（14）可知，信噪比的值越大，均方根誤差越低，維持率越高，則預估信號就越接近于原始信號。

通過MATLAB 仿真計算后，將各種閾值函數與固定閾值結合在一起，得到數據見表1。 將各種閾值函數與多尺度閾值結合在一起，得到數據見表2。

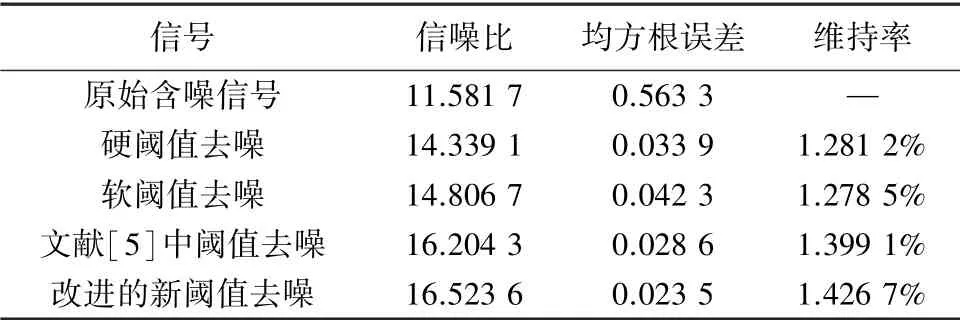
表1 固定閾值與各種閾值函數結合降噪效果Tab.1 Noise reduction effect of fixed threshold combined with various threshold functions

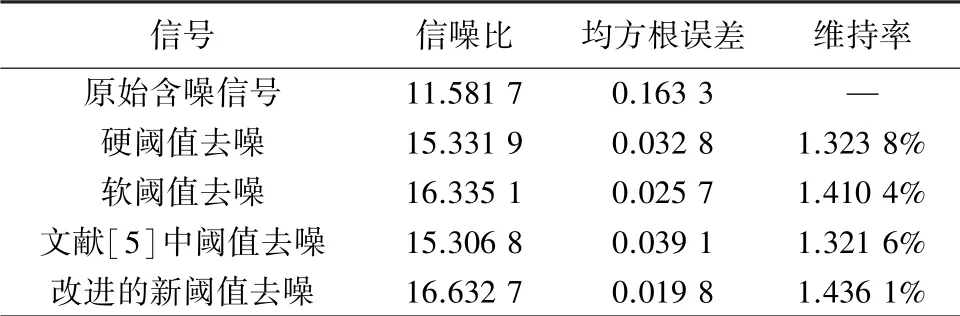
表2 多尺度閾值與各種閾值函數結合降噪效果Tab.2 Multi－scale threshold combined with various threshold functions to reduce noise

由兩表對比可以看出，多尺度閾值與各種閾值函數結合降噪相比于各閾值函數與固定閾值相結合取得的信噪比略高，均方根誤差相對降低，維持率也相對提高。 證明了將多尺度閾值與改進的新閾值函數結合的降噪方法能獲得更大的信噪比，取得了更好的降噪效果。

4 結束語

在熱泵機組監控過程中，熱泵電機振動信號的降噪具有重要意義。 本文針對軟閾值和硬閾值函數存在的不足，提出了一種結合多尺度閾值的新閾值函數。 通過仿真實驗，分別采用新閾值函數和軟閾值、硬閾值函數對采集的熱泵電機振動信號進行降噪處理。 實驗結果證明了新的閾值函數在熱泵電機信號降噪過程中具有信噪比較高和均方根誤差較低的特點，具有重要的工程實踐意義。