基于量子神經網絡的地層對比研究①

王偉，趙婭，李盼池

(1.廣東石油化工學院 石油工程學院，廣東 茂名 525000；2.東北石油大學 計算機與信息技術學院，黑龍江 大慶 163318)

地層對比是油氣田勘探與開發工作中進行油藏描述及多井評價的重要組成部分[1,2]。地層對比最常用的方法是根據單井測井曲線特征在某一層段上的最大相似性原則來完成的。但該方法在油田開發后期，對比工作量大，并且陸相三角洲沉積橫向砂體不穩定、相變快，過度依賴專家經驗，限制了對比結果的正確性。近年來，基于測井曲線的人工智能自動地層對比方法逐漸成為領域研究熱點，其中較流行的方法有：人工智能方法[3-5]、字符串動態匹配算法[6-8]、BP神經網絡方法[9-13]、智能算法[14-18]等。這些方法有一定的成效，甚至已經應用到商業化軟件上，但其效果依然難以讓人滿意。如目前應用效果最好的BP神經網絡方法識別準確度高，但是在網絡模型訓練時需要大數據樣本，這對于數據樣本少的情況不適用。

針對這些存在的問題，本文提出一種基于量子神經網絡(Quantum Neural Networks，QNN)的多井井間小層自動對比方法。利用測井曲線及其統計特征數據構造網絡模型，實現基于QNN的小層自動對比。旨在構建具有收斂速度快、逼近精度高、泛化能力強等優點的網絡模型，在兼顧準確性的前提下，提高地層對比工作的效率。

1 量子神經網絡模型及算法

研究表明，人腦信息處理的過程可能與量子現象有關，大腦中可能存在量子力學效應，量子系統具有與生物神經網絡相似的動力學特征[19]。量子神經網絡是量子計算和神經計算相融合的結果，將神經網絡和量子計算理論相結合能更好地模擬人腦的信息處理過程。量子神經網絡中的“量子”，是指量子計算的某些原理和方法。在傳統神經網絡中引入“量子”的目的，是借助量子計算的某些機制(如量子比特的旋轉)來提升網絡的逼近及泛化能力。

1.1 量子神經元模型

圖1 量子神經元模型 圖2 量子神經網絡模型

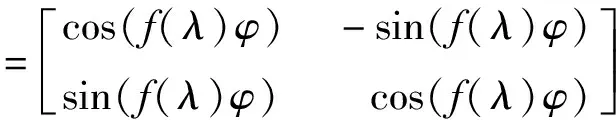
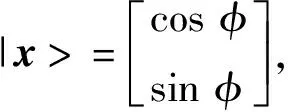
此時，量子神經元的輸出為

(1)

1.2 量子神經網絡模型

本文采用的三層量子神經網絡(見圖2)，其中輸入層、隱層和輸出層分別有n、p、m個量子神經元，網絡輸出為量子神經元處于狀態|1>的概率幅。

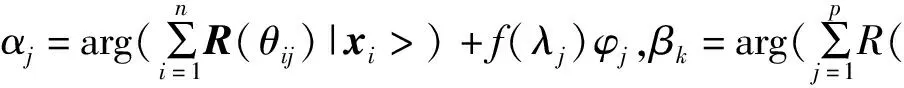
|hj>=[cosαj，sinaj]T

(2)

yk=sinβk

(3)

量子神經網絡需要訓練的參數包括：γk，ξk，?jk，λj，φj，θij，這些參數可以通過梯度下降法訓練。參數調整規則可統一描述為β(t+1)=β(t)+ηΔβ(t+1)，其中β分別為θij、?jk、φj、ξk、λj和γk，而η為學習速率。

2 基于QNN的地層對比

本文采用Matlab語言進行QNN網絡模型的編程，對朝陽溝油田6口已經人工分層的標準井共計126個小層進行了地層對比仿真實驗，其中5口井(105個小層)用于訓練，1口井(21個小層)用于測試。再利用構造的模型對全區366口井進行地層對比。將地層對比分為二級地層對比和三級地層對比。二級地層對比，小層類別包括10類：F11(包括F111～F115)、F12(包括F121～F122)、F13(包括F131～F132)、F14、F15(包括F151～F152)、F16(包括F161～F162)、F17(包括F171～F172)、F21(包括F211～F212)、F22(包括F221～F222)、F23；三級地層對比包括21個小層類別。

2.1 特征參數選擇

選擇對巖性敏感的測井曲線作為進行地層對比的主要依據，此外反應各井單砂層測井曲線形態的一些特征向量值，也是優秀的地層對比指標[20]。本文選定地層對比的特征參數有：小層厚度，自然伽馬(GR)、自然電位(SP)、聲波時差(AC)、深側向電阻率(LLD)4條測井曲線的均值，中位數、相對重心X、相對重心Y、鋸齒數、方差變差等5種統計特征，組成特征向量，構造井間小層對比的輸入樣本。所選的特征參數有助于網絡模型構造高質量的訓練樣本，極大地提高了網絡模型的訓練能力及泛化能力。

2.2 測井曲線濾波去噪和歸一化

原始測井曲線數據存在的噪聲，會影響QNN的識別效果，因此需要進行濾波處理。本文采用經典的沃爾什濾波方法。該方法先對測井曲線實施離散沃爾什變換[21，22]，忽略某些高頻分量之后，再進行反變換重構原曲線。為消除不同量級數據之間的相互影響，對所選4條曲線數據進行歸一化處理。

2.3 構造樣本數據

參與對比的10個特征參數中，小層厚度可根據測井解釋結果獲得；自然伽馬、自然電位、聲波時差、深側向電阻率從測井曲線上獲取；中位數、相對重心X、相對重心Y、鋸齒數、方差變差為單個數值，它們均來自于自然伽馬曲線的離散數據[23]。

2.4 樣本數據量子態描述

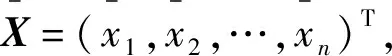
|X>=[|x1>，|x2>，…，|xn>]T

(4)

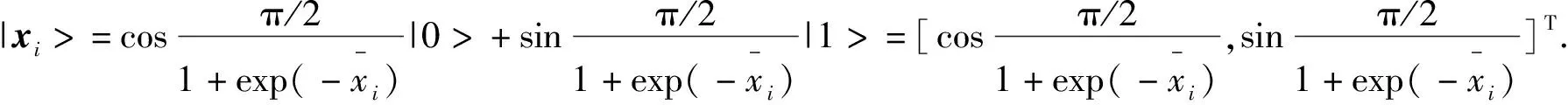
對于所有實值樣本，應用式(4)即可轉換為可以提交QNN訓練的量子樣本。

2.5 構造QNN模型

將樣本數據分為訓練集和測試集兩部分，訓練集用于QNN的網絡訓練，使網絡模型逼近樣本特征和小層類別之間隱含的復雜非線性映射關系；測試集用于檢驗QNN的泛化能力。關于QNN模型參數設置，輸入節點個數等于小層特征參數個數(10個)；網絡的輸出為小層類別，只用1個輸出節點即可；隱層節點一般沒有確定規律可循，通過多次實驗來獲取。訓練后的網絡模型即可用于目標小層類別的對比。

本文方法是以整口井為單位進行小層識別的，對于處理好的單口測試井數據，若該井沒有斷層，則輸出小層類別應滿足固定層序；若某層違反了層序，則該層可認為是斷層。

2.6 與BP神經網絡模型應用對比

為驗證QNN在地層對比方面的性能，本文采用QNN與BP神經網絡對比。為了使對比更加充分，本文使QNN和BP分別在不同隱層節點和迭代次數下獨立運行100次，然后取平均識別率作為對比指標，隱層節點具體取1，2，…，10，迭代次數分別為50，60，80，100，120，140，160，180，200。三級地層對比QNN和BP網絡模型對測試集的識別實驗結果見表1。

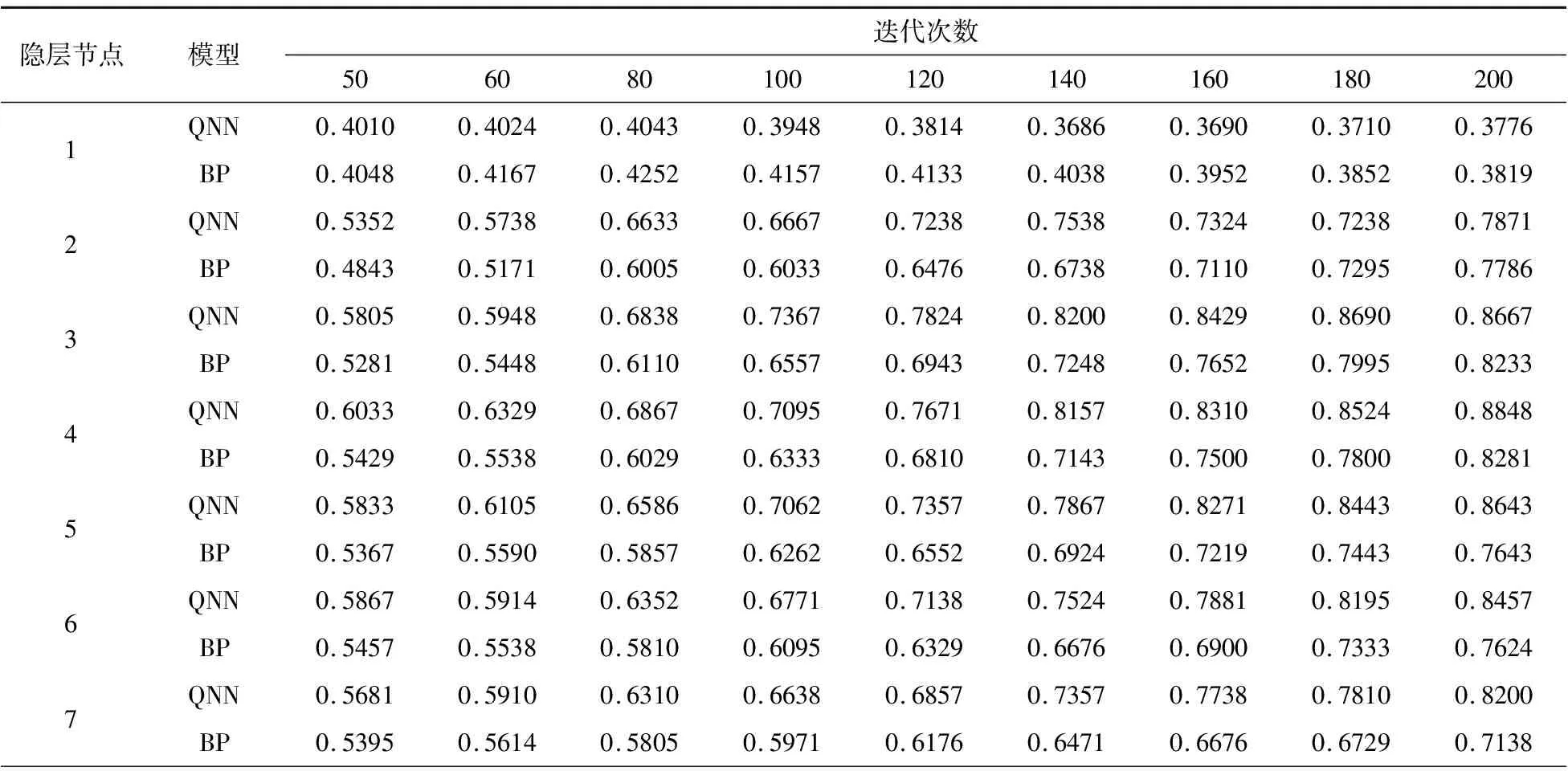
表1 三級地層對比QNN和BP網絡模型對測試集的識別結果

由表1可知，對于三級地層對比，當隱藏節點為4，迭代次數大于140時，QNN識別率均在80%以上，最高值為88.48%，而BP網絡識別率最大值僅為82.81%。QNN優于BP神經網絡，這主要是在QNN中引入了量子機制。在QNN中，通過量子旋轉門和受控量子旋轉門的協同作用，增強了網絡的學習能力、模式信息概括能力、函數逼近能力以及泛化推廣能力，從而使QNN在少量數據樣本的情況下依然表現出良好的適應性。

3 基于QNN的地層對比結果

利用該模型對全區366口開發井進行地層對比工作，三級小層對比的正確率最高可達88.48%。以F142-X井為例，對該井的10個二級分層和21個三級分層進行識別，結果見圖3。

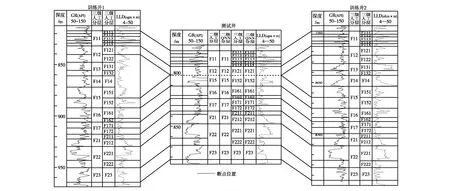
圖3 測試井人工分層與QNN分層結果對比

由圖3可知，該井的二級分層識別均正確，僅三級分層F111小層被識別成F112。造成原因是F111的地層厚度小，導致所含的特征測井曲線數據量不足，這說明要達到較高的識別率，地層需要一定的厚度，以增加測井曲線數據量。根據識別的結果與正常的層序，可以有效地確定該井的斷點位于F12與F15之間(F122～F151斷失)。

4 結論

(1)量子神經網絡算法通過量子旋轉門和受控量子旋轉門的協同作用，增強了網絡的學習能力、模式信息概括能力、函數逼近能力以及泛化推廣能力，從而使QNN較其它智能算法，在少量數據樣本的情況下依然表現出更好的適應性。

(2)根據QNN識別后所輸出小層層序是否間斷，能夠判斷該井是否存在地層斷失情況及斷點位置。

(3)利用構建的QNN網絡模型，對長46地區366口井進行地層對比，三級小層對比的正確率可達88.48%，證明采用量子神經網絡解決地層對比中工作量大、砂體相變快、地層斷失等問題是可行、有效的。