基于尖點突變理論的隧道工程壓力錨桿穩定性研究①

李文劍，李浩軍，朱艾路

(中山市住房和城鄉建設局，廣東 中山 528403)

隨著我國公路工程、市政工程建設規模的不斷擴大，需要建造越來越多的隧道工程。壓力錨桿屬于隧道工程的重要初期支護體系，而在隧道結構中錨桿受力復雜。筆者通過引入突變理論的尖點突變模型，用該機理分析隧道錨桿力學特性并進行穩定特性研究。首先對國內的相關研究進行回顧。周平等利用突變理論對隧道局部失穩進行預測研究[1]。張業民以突變理論為基礎研究了尖點突變模型在巖土力學本構模型的可行性和工程應用[2]。胡晉川利用尖點突變理論分析黃土邊坡的穩定性[3]。張業民、李文劍等利用數值模擬方法研究隧道錨桿施工過程力學特性[4-8]。張業民、李順群等研究了細長桿屈曲后位移的計算方法[9,10]。

本文以壓力型錨桿為研究對象，對受壓錨桿在圍巖的水平剪力等情況下錨桿桿體可能發生幾何屈曲變形而影響結構承載力的情況，利用尖點突變理論建立模型，從而分析錨桿在受壓狀態下的穩定性,為后隧道加固和支護參數優化提供理論支撐[7-9，11]。

1 錨桿力學模型

以壓力型錨桿為研究對象。壓力型錨桿桿體本身受到隧道圍巖擠壓和剪切力作用、注漿壓力、與周圍圍巖共同作用的摩擦力等沿著桿體長軸方向的拉拔、懸、吊力等，統一把這些受力的合力歸結為水平力Q和垂直壓力P的作用。錨桿需經鉆機鉆孔圍巖后的條狀細長空間內植入故錨桿兩端無彎矩發生，不妨按兩端鉸支考慮。當P、Q力共同作用達到一定數值時，壓力錨桿可能會突然產生屈曲，這對于結構承載力會有一定程度的影響。從圖1的錨桿分析模型推導，P=Pcr=EIπ2/L2，而水平力Q=0時，錨桿在空間內可能處于穩定狀態，但此時隨著力P變化可能出現屈曲。錨桿受到水平力Q的作用，壓力錨桿就可能沿水平方向的某一邊凸起，此時壓力錨桿發生屈曲現象[2,9,10]。

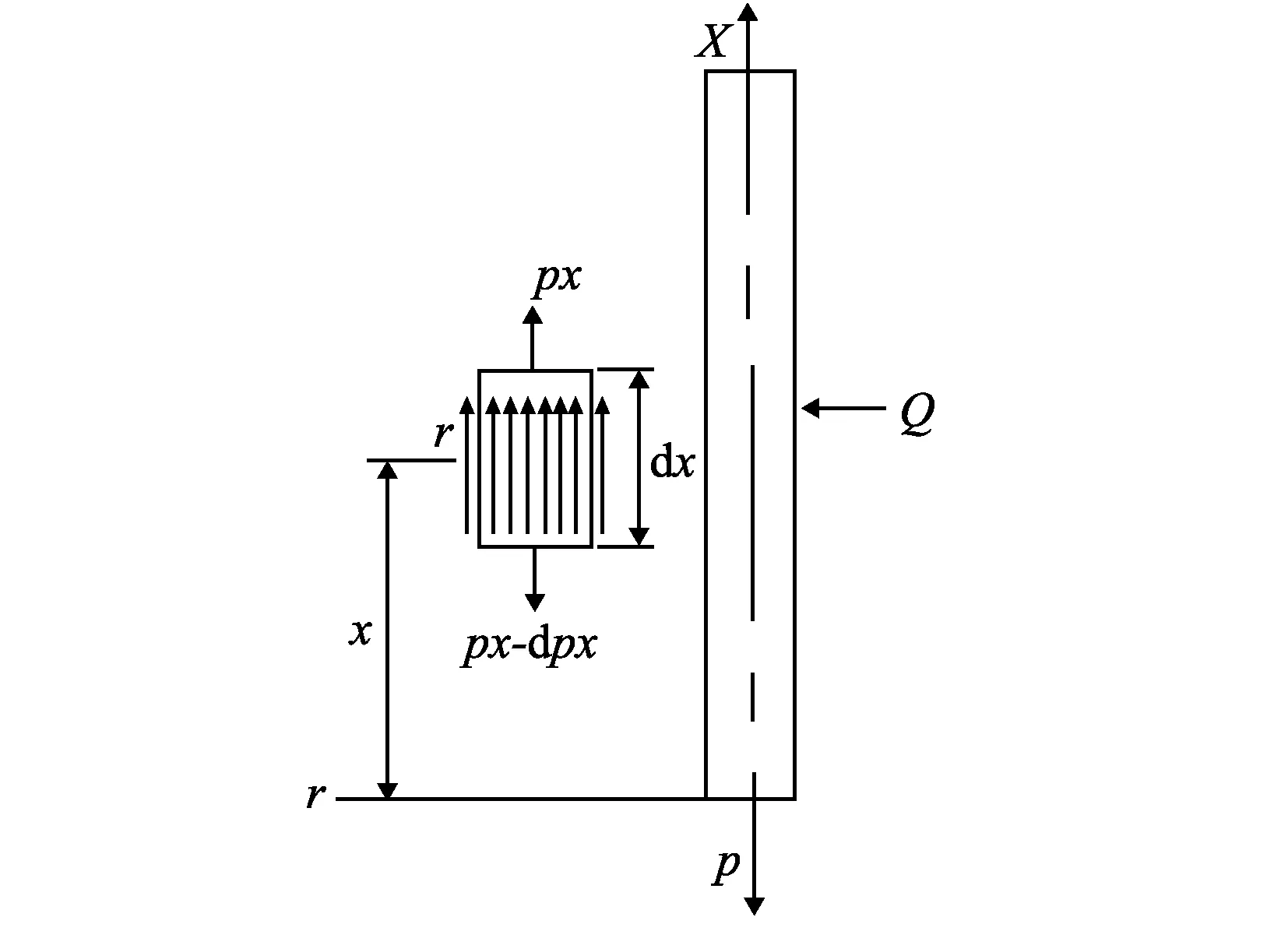
圖1 錨桿分析模型

壓力錨桿穩定狀態由水平力Q和垂直力P來決定，壓力錨桿的幾何性狀失穩可以用尖點突變理論來描述。對于壓力錨桿發生屈曲問題來說，即垂直力P與水平力Q，這兩者作為二維控制變量，將表征事物質態變化參量的壓力錨桿中點位移δ作為一維狀態變量。這3個變量組成的三維空間模型如圖2所示，曲面方程即為基于壓力錨桿的尖點突變模型方程[10]。

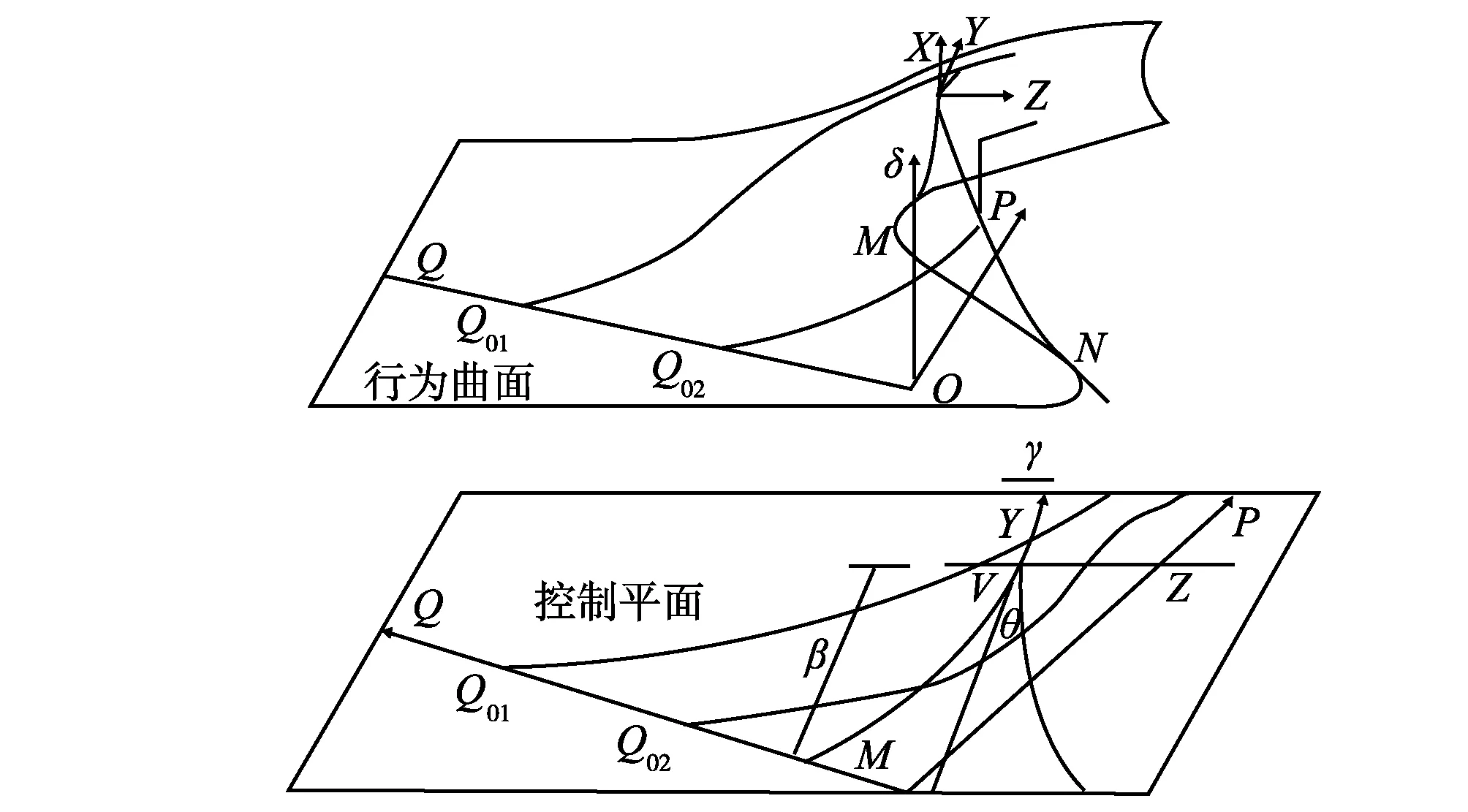
圖2 (δ,Q,P)坐標下的尖點突變模型

2 壓力錨桿尖點突變模型

由突變理論可知尖點模型的勢函數可表達為V(x)=x4+ux2+vx=0

(1)

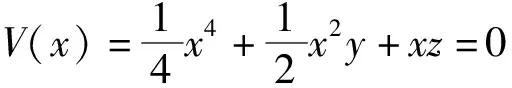
(2)

控制平面內的分支曲線方程 4y3+27z2=0

(3)

將標準方程的坐標經旋轉與平移至O(δ,Q,P)的坐標系中可得下列方程組：

(4)

式中：α，β，γ為點O(δ，Q，P)坐標系中的位置坐標值；aij為原坐標對新坐標的方向余弦。由于模型中設δ軸與x軸平行，故a11=1。通過上述坐標變換后可求得曲面于新坐標系O(δ，Q，P)內的方程式為

f(δ，Q，P)=(δ+a12Q+a13P-α)3+(a21δ+a22Q+a23P-β)×

(δ+a12Q+a13P-α)-a31δ+a32Q+a33P-γ=0

(5)

坐標變化的附加條件為

(6)

同為右手系時需滿足：

(7)

引入邊界條件，在O(δ，Q，P)坐標系中當δ=0、Q=0時即表示P軸，故則方程f(δ，Q，P)=0，此時應為線性函數。f(0，0，0)=0，將上述邊界條件及附加條件代入式(4)，最終可以求得：

(8)

α=tanθ

(9)

又由式f(0，0，0)=0求得：

α3-αβ-γ=0

(10)

將式(8)代入式(5)得：

f(δ，Q，P)=(δ-α)3+(Qcosθ+Psinθ-β)×(δ-α)-(-δsinθ+Qcosθ-γ)=0

(11)

將式(9)，式(10)代入式(11)得：

f(δ，Q，P)=(δ-α)3+α3+δ(Q-β)cosθ-P(α-δ)sinδ=0

(12)

β′=β/cosθ

(13)

有關參數的確定：α為細長桿發生屈曲時的中點位移，參考張業民等[2]研究成果可取為0.3L。由于θ點表示失穩因子為零的場地，只要該處經受一微小的側向干擾力，即可導致發生屈曲，故應認為原點O亦位于分歧曲線上，則由分歧曲線標準方程式獲得

4β3-27γ2=0

(14)

式中：β值可由式(11)、式(14)及α值確定。

3 工程實例

3.1 壓力錨桿驗算

以廣東省中山市某城市快速路交通隧道工程為背景，取該隧道工程應用系統錨桿的壓力注漿型錨桿為工程研究對象。其性能參數如下：σp=200 MPa，E=210 GPa，λp=100，錨桿直徑d=22 mm，則假設桿長為L，該隧道工程應用實際錨桿理論設計桿長L最小值為3.5 m>0.55 m，屬細長桿。經數值計算，該錨桿構件的承載力為65.313 kN，計算結果f=179.06 N/mm2。小于現行規范《混凝土結構設計規范》(GB 50010—2010(2015版))規定的極限屈服值fstk=420 N/mm2。從偏安全角度考慮計算臨界狀態設當桿長L=0.5 m 時；α=0.15 m，β=0.050625，若Q=0.1 kN，桿體受到水平的剪切力就可發生錨桿水平失穩。

可見在無水平約束時桿體會發生失穩變形且遠未達到屈服強度，則存在一定的強度儲備未有完全發揮。如若加固周圍圍巖、通過注漿增加水平約束力后錨桿的承載力可大幅發揮壓力錨桿剩余承載力。

3.2 實測對比

根據孫艷、張業民等[10]的研究實測數據成果：L=0.5，δ=0.159，P=42.721，f(δ，Q，P)=0.07。將數據代入推導出的尖點突變模型方程式中，結果與實測吻合較好。

3.3 錨桿環向穩定性分析

隧道拱頂錨桿一般均為沿環向均勻布置。若壓力錨桿在穩定性良好的圍巖中沿環向布設，通過對隧道壓力注漿和錨桿擠壓黏結作用，加固隧道開挖面以外一定范圍內的土體，提高其自身結構抗力性能并在拱頂一定區域內形成承載“拱圈”。拱圈的形成使錨桿桿體水平位移受到約束，相當于水平力Q有相互作用力和反作用力，促進錨桿穩定則對于支護結構整體穩定性有利。

錨桿本身作為支撐構件與隧道初期支護噴砼結構結合形成機動結構，兩者可有機地融合，形成共同工作的防護結構而限制洞周收斂變形。通過壓力注漿錨桿的施設，達到加固洞周以外一定范圍內圍巖的目的，同時可以形成結構拱，可較有效地防止隧道滲漏和增強結構穩定。根據驗算成果及時調整和反饋錨桿的布設長度、注漿位置、注漿深度，對于合理使用錨桿增強結構的整體穩定性有積極意義。

4 結論

錨桿的理論分析可以是多方面的，不僅與計算模型相關，而且與錨桿計算理論有關。考慮壓力錨桿破壞的突發性和瞬時性，引入突變理論將勢函數化簡為尖點突變模型的標準形式，得到錨固體沿軟弱面滑動突變失穩的充要力學條件。通過引入突變理論的尖點突變模型，對隧道工程壓力錨桿支護的復雜性建立壓力錨桿力學模型，利用突變理論的基本公式推導出壓力錨桿幾何失穩的尖點突變模型，并且通過工程實例驗算與實測對比驗證該理論方法可行。

通過分析錨桿力學性能并未完全發揮，其強度富余的空間相對較大。若通過圍巖加固、注漿等方式為錨桿提供水平向Q的約束力則對于壓力型錨桿發揮富余強度有著積極的意義。同時能夠加固圍巖，增加錨桿桿體與周圍圍巖的相互摩擦咬合力，從而提高巖土體的整體穩定性。如果采用加長型壓力錨桿則桿體更加深入圍巖內部，從而更加能夠發揮桿體的拉拔、懸挑作用，但能有效抑止拱頂受拉破壞區的形成和塑性區的連通。

以突變理論為基礎研究隧道壓力型錨桿的作用效果，從理論角度探求錨桿穩定性問題，從尖點突變模型入手推導出壓力錨桿尖點突變模型。實測與理論推演的結果基本相符。

環向的多重注漿后錨桿聚集在一起產生水平約束力Q，不僅加固洞周以外一定范圍內的圍巖后形成一定的連續承載拱圈作用，而且還可以協助發揮錨桿的剩余強度，且越靠近中點效果越顯著。可為進一步研究壓力型錨桿與周圍構筑物的共同作用理論和壓力型錨桿的工程應用、結構加固提供理論支撐。

根據理論驗算可以及時調整反饋錨桿的布設長度、注漿位置、注漿深度等參數，可指導隧道支護結構布設的同時優化結構設計。對于進一步研究錨桿的破壞形式和受力形式作理論鋪墊，為下一步隧道工程壓力錨桿實體試驗、隧道現場監測點位置作出理論指引。