基于加速度信號的吊弦斷裂檢測方法
聶晶鑫
(中鐵第一勘察設計院集團有限公司,西安 710043)
1 引言
接觸網的工作狀態直接關系著列車的運行安全.接觸網沿線路露天架設,長期受環境、氣候等自然因素以及車輛受電弓的沖擊作用,容易發生故障[1].吊弦是接觸網的關鍵部件,起著固定接觸線的作用.當列車行駛時,受電弓作用于接觸線,引起吊弦和承力索的舞動.這種方式日復一日地運行,在交變應力作用下可能發生吊弦斷裂事故,威脅行車安全,如武廣線在2011 年發現吊弦斷裂問題多達60 處[2].因此,對吊弦進行在線監測,及時發現吊弦故障,是保障接觸網安全的有力措施.
近年來,國內外針對接觸網運行狀態,研究了基于多種技術的檢測方法,總體來說,可分為接觸式及非接觸式檢測方法.非接觸式方法通過圖像識別技術從外觀上發現吊弦故障.文獻[3]以4C 巡檢高清圖像為對象,基于卷積神經網絡實現接觸網七種關鍵區域(包括吊弦)的缺陷檢測,但這種方法的檢測精度有限,容易出現誤報和漏報.于是人們開始研究接觸式檢測方法.文獻[1]從接觸網—受電弓的耦合動力學角度出發,分析了不同接觸網結構故障的動力學響應特征,運用支持向量機進行故障特征識別.文獻[4]基于混合濾波器對含噪信號進行消噪處理,對信號進行小波變換,根據模極大值原理計算Lipschitz 指數,實現斷線故障的檢測.但是這些方法故障識別率有待進一步提高.
本文建立蘭新高速鐵路弓網動態仿真模型[5],通過有限元方法對模型進行求解,獲取在脈動風和受電弓同時作用下的接觸網正常和發生故障時接觸線和承力索監測點的加速度數據,然后運用EEMD 提取加速度信號的多種特征,建立吊弦斷裂故障診斷L1/2-LR 模型.實驗結果表明,所建立的檢測模型,在脈動風和受電弓共同作用工況下準確率達到97.25%.
2 數據仿真
2.1 仿真模型
本文對蘭新高鐵里程為K3066+568.795 ~K3065+588.795 的接觸網試驗段建立弓網動態仿真模型[5].受電弓的仿真使用三歸算質量-阻尼-剛度模型,接觸網的相關設計參數如表1 所示.
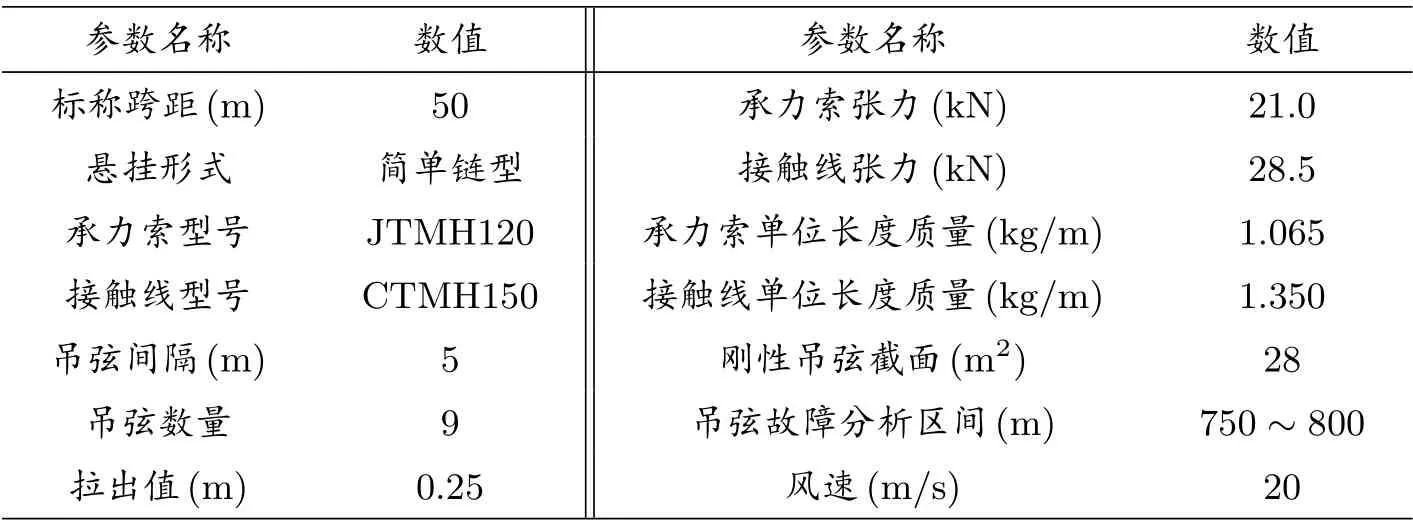
表1: 接觸網設計參數
2.2 傳感器安裝
接觸網每跨長度為50 米,共有9 個吊弦,每隔5 米在承力索和接觸線之間安裝有1 根吊弦.通過在接觸網上安裝加速度傳感器提取兩種工況下的接觸網力學響應,加速度傳感器的安裝位置如圖1 所示.
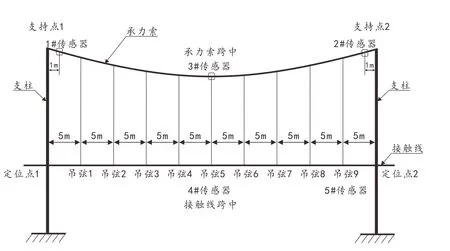
圖1: 接觸網力學性能響應數據提取點
1#加速度傳感器:承力索上支持點1 內側1m 處;
2#加速度傳感器:承力索上支持點2 內側1m 處;
3#加速度傳感器:承力索上跨中位置;
4#加速度傳感器:接觸線上跨中吊弦5 處;
5#加速度傳感器:接觸線上跨中吊弦9 處.
2.3 仿真工況
為獲取1#~5#檢測點的加速度,本文對列車以250 km/h 的速度行駛時,接觸網試驗段受電弓和脈動風同時作用下,吊弦無斷裂和21 跨的跨中位置吊弦斷裂兩種工況進行仿真,獲取了400 組數據,其中包括兩種工況各200 組.加速度傳感器的采樣頻率為277 Hz,每條樣本采集時間為17 秒,共4800 個數據點.每組數據包括5 個加速度傳感器所采集的垂直、水平方向振動加速度.
3 基于EEMD 分解的特征提取
通過對脈動風和受電弓同時作用下,跨中吊弦斷裂及沒有斷裂情況下的加速度信號進行分析,發現傳感器采集的加速度信號數據是非線性非平穩的,所以需要采用EEMD 方法,將原始信號數據分解為多個本征模態函數,再提取本征模態函數的能量熵、平均熵和奇異熵特征.
3.1 EEMD 分解
經驗模態分解方法(EMD)[6]將一個頻率不規則的波化為多個單一頻率的波加殘波的形式,單一頻率的波稱為本征模態函數(IMF),但EMD 存在模態混疊缺陷.為了克服這一問題,本文采用EEMD[7]進行加速度信號特征提取.EEMD 分解以EMD 理論為基礎,在原始信號中多次添加白噪聲.因為白噪聲具有均勻頻率分布特性,可以改變信號中極值點分布,有利于信號的抗混分解,有效地抑制了模式混淆.其分解步驟見算法1.
算法1EEMD 分解
輸入:原始信號
輸出:多次分解下的平均IMF
步驟3:獲得多次分解下的平均IMF,以消除各分量重殘余的白噪聲
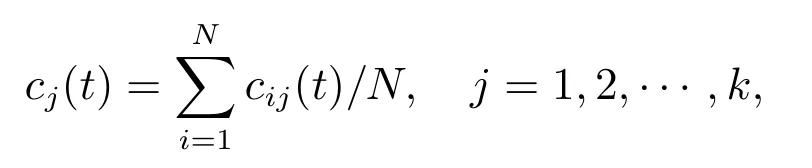
其中cj(t)為對原始信號進行EEMD 分解后所得的第j 個IMF.
3.2 信息熵特征
將EEMD 和信息熵結合,能達到信息融合的目的,可有效地分析信號中的突變情況.這里主要采用IMF 的三種熵測度,即IMF 能量熵、IMF 奇異熵和IMF 平均熵[8].
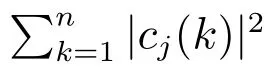
1) 能量熵的計算
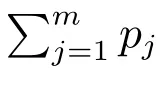
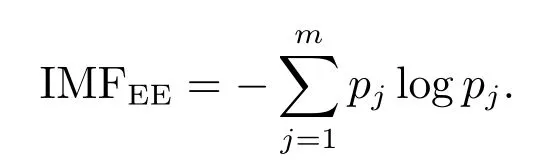
2) IMF 奇異熵
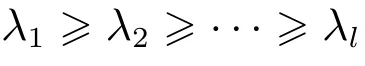
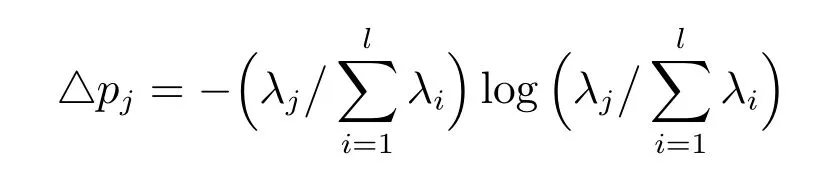
表示第j 個IMF 分量的奇異熵,則整個信號的奇異熵定義為
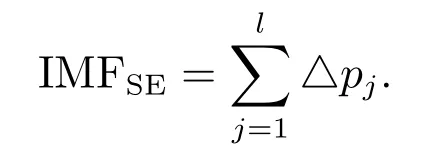
IMF 奇異熵反映信號經EEMD 分解出的尺度空間中IMF 分量能量的分布的不確定性.如果信號比較簡單,能量就集中在少數幾個IMF 分量上,奇異熵就越小;如果信號比較復雜,能量就越分散,奇異熵就越大.
3) 平均熵的計算
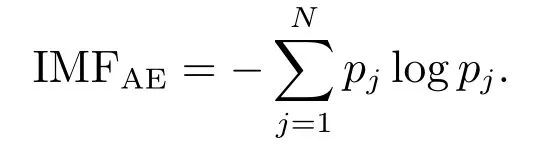
IMF 平均熵體現信號在IMF 分量上的平均復雜度,與時間、頻率變化無關.能量分布越是均勻,平均熵就越大.
3.3 特征提取
加速度信號經過EEMD,形成多個本征函數IMF,計算各IMF 與原始信號的皮爾遜相關系數,挑選出有效的IMF 分量.本文設置閾值為0.1,即取皮氏積矩相關系數大于0.1 的IMF 分量作為有效分量來計算IMF 熵特征.
設X 和Y 為兩個向量,xi,yi(i = 1,2,··· ,N)為各自的分量,其皮氏積矩相關系數r 計算公式為
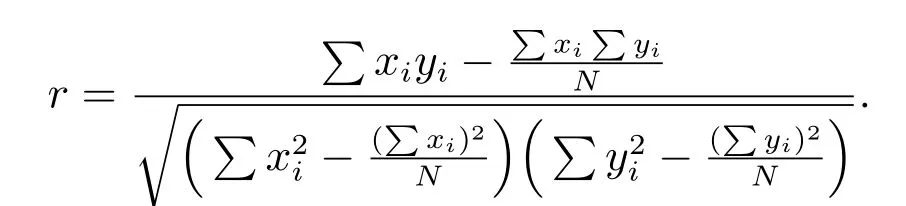
應用算法1,加速度信號經過EEMD 分解為12 個IMF 分量.在受電弓和脈動風同時作用下,各個加速度的IMF7–IMF12 分量和原信號的相關系數都小于0.1,可以忽略.因此選取經EEMD 分解后的1 ~6 的IMF 分量.承力索支持點1 垂直加速度、承力索跨中垂直加速度、承力索支持點2 垂直加速度、承力索支持點1 水平加速度、承力索跨中水平加速度和承力索支持點2 水平加速度的IMF1–IMF6 分量與原信號的相關系數見表2.
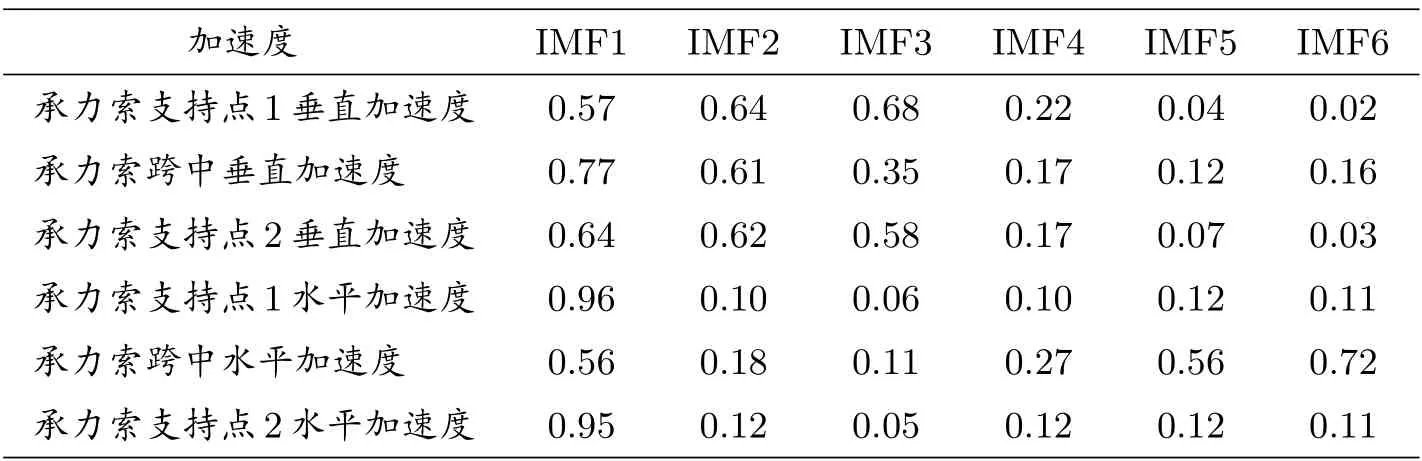
表2: IMF 分量與分解前信號的相關系數
選取1#~5#傳感器的10 個加速度信號的1 ~6 的IMF 分量,計算其IMF 能量熵、IMF 奇異熵、IMF 平均熵,共30 個特征.
4 吊弦斷裂檢測L1/2-LR 模型
通過EEMD 分解提取的30 特征可能存在冗余的變量,所以需要進行特征選擇,找到對故障識別具有顯著影響的變量進行故障診斷.本文結合L1/2正則化很強的稀疏性和Logistic 回歸良好的分類性能,建立L1/2-LR[9-12]吊弦斷裂檢測模型.
4.1 L1/2-LR 模型
L1/2-LR 正則化優化模型如下
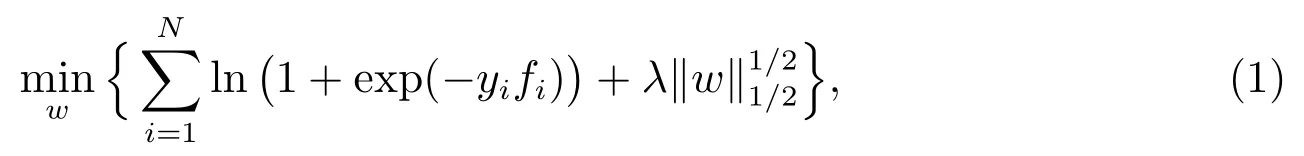
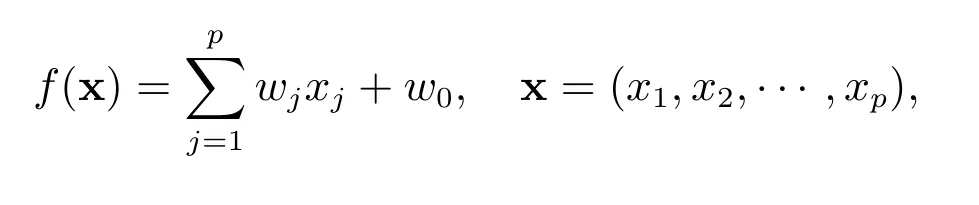
其中p 為向量x的維數,N 為樣本個數,xi=(xi1,xi2,··· ,xip)為第i 個樣本的屬性向量,yi為樣本xi的標號,取值為?1 或1,分別代表樣本xi發生吊弦斷裂和未發生吊弦斷裂,w =(w0,w1,w2,··· ,wp)為待求未知向量,λ>0 為正則化常數.
4.2 L1/2-LR 模型求解算法
L1/2-LR 分類模型是一種非凸優化模型,可應用閾值迭代算法求解.
算法2L1/2-LR 的閾值迭代算法
輸出:分類判別函數
步驟1:初始化w0=(0,0,··· ,0)T,訓練步數t=0;
步驟2:按公式
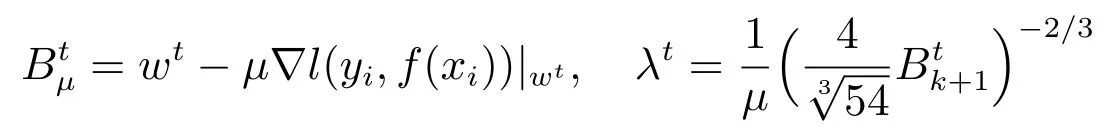
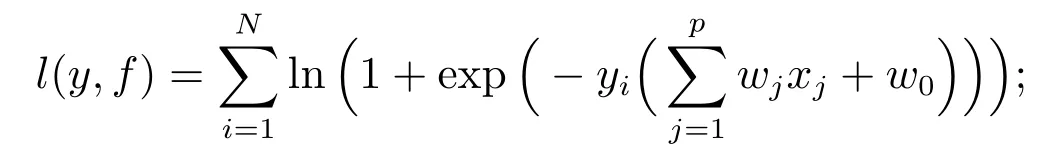
步驟3:令λ=λt,更新wt+1=Hλμ(Btμ),其中
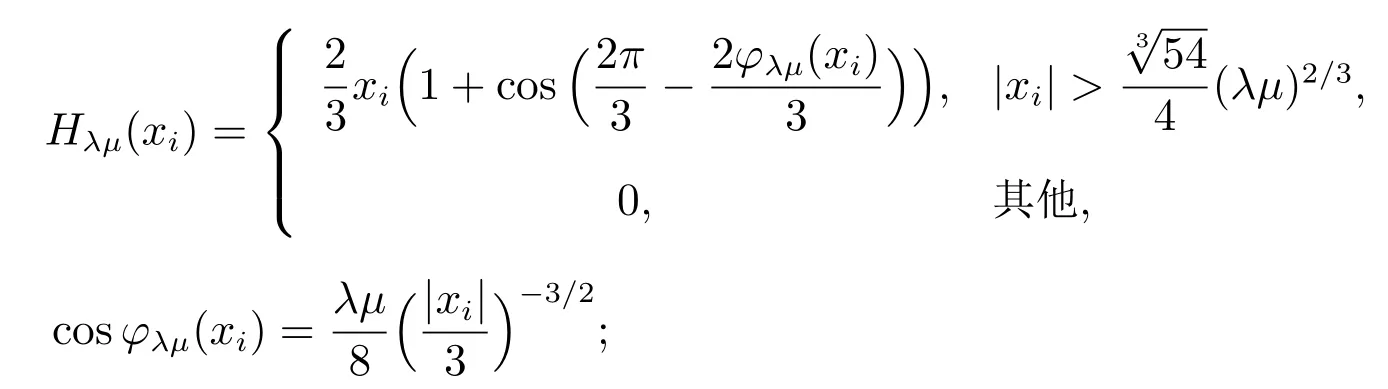
4.3 L1/2-LR 模型求解
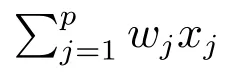
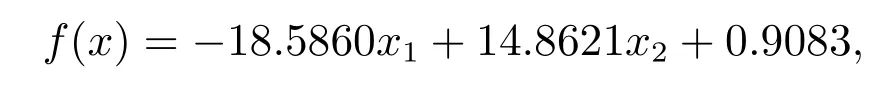
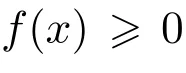
5 結論
本文提出了一種基于加速度信號EEMD 的接觸網吊弦斷裂檢測方法.本方法通過對接觸網承力索和接觸線上采樣點的加速度信號進行EEMD 分解、計算本征模態函數,對其提取能量熵、平均熵和奇異熵,以這三種類型的熵特征建立了吊弦斷裂檢測L1/2-LR 模型.實驗表明,在脈動風和受電弓同時作用的工況下,所得到的檢測方法對吊弦斷裂檢測的準確率可達97.25%.本文提出的L1/2-LR 模型,具有變量選擇作用,發現只需采集承力索跨中位置處的垂直加速度和中水平加速度,分別計算其能量熵、平均熵,就可以以很高的精度和計算效率檢測跨中吊弦是否斷裂.

