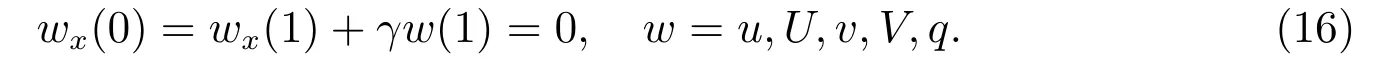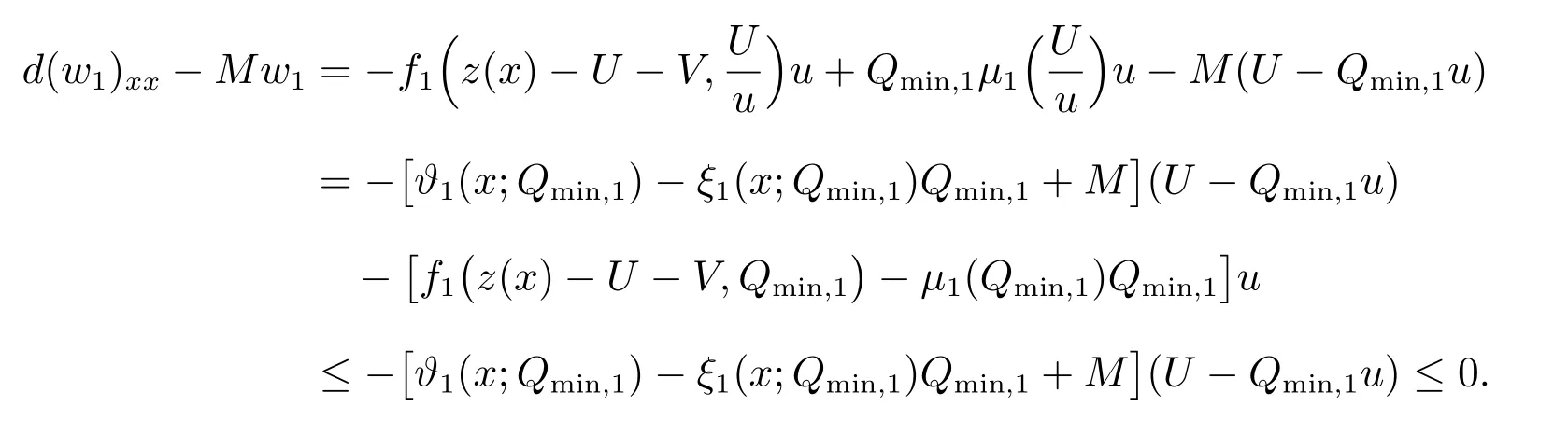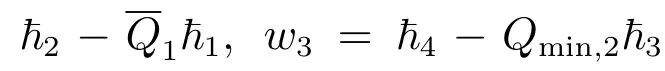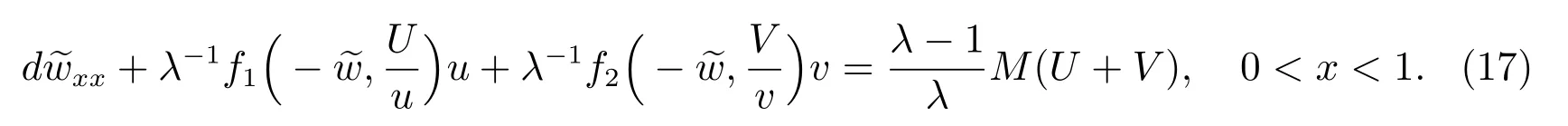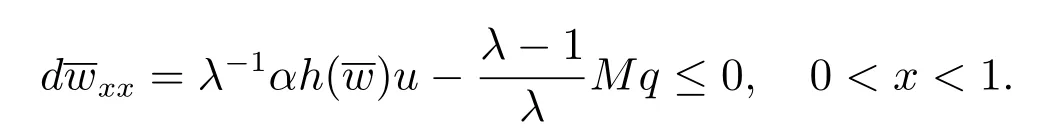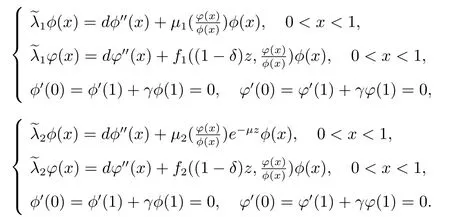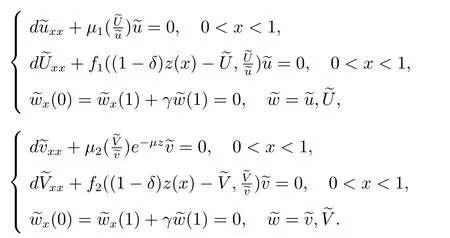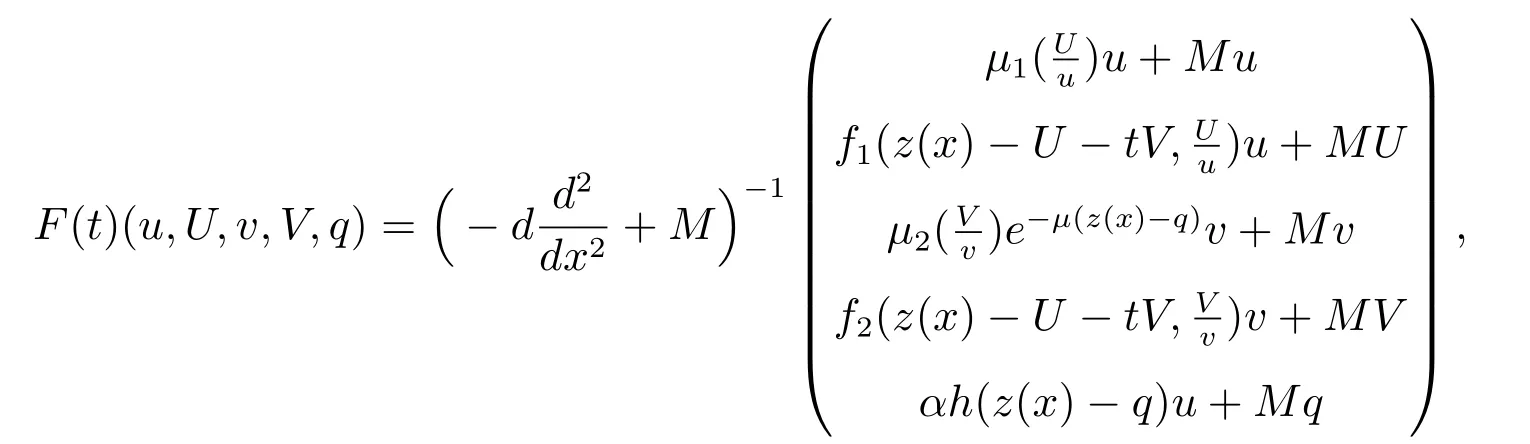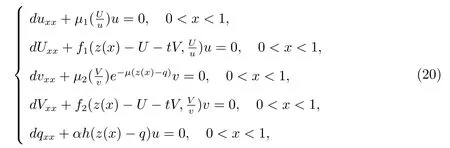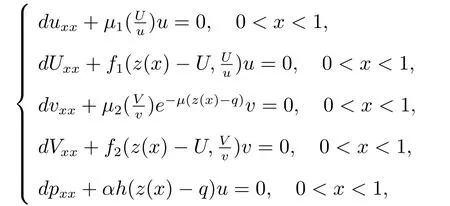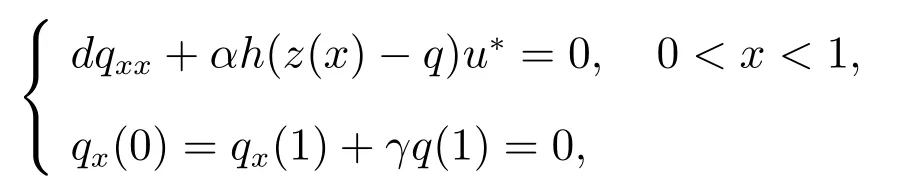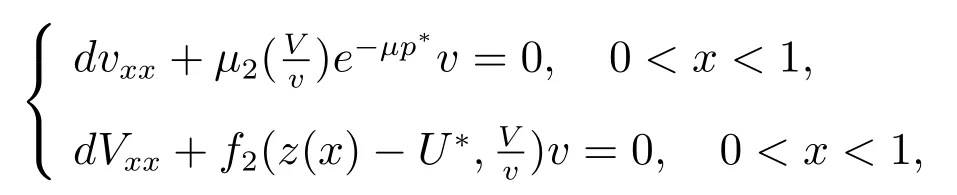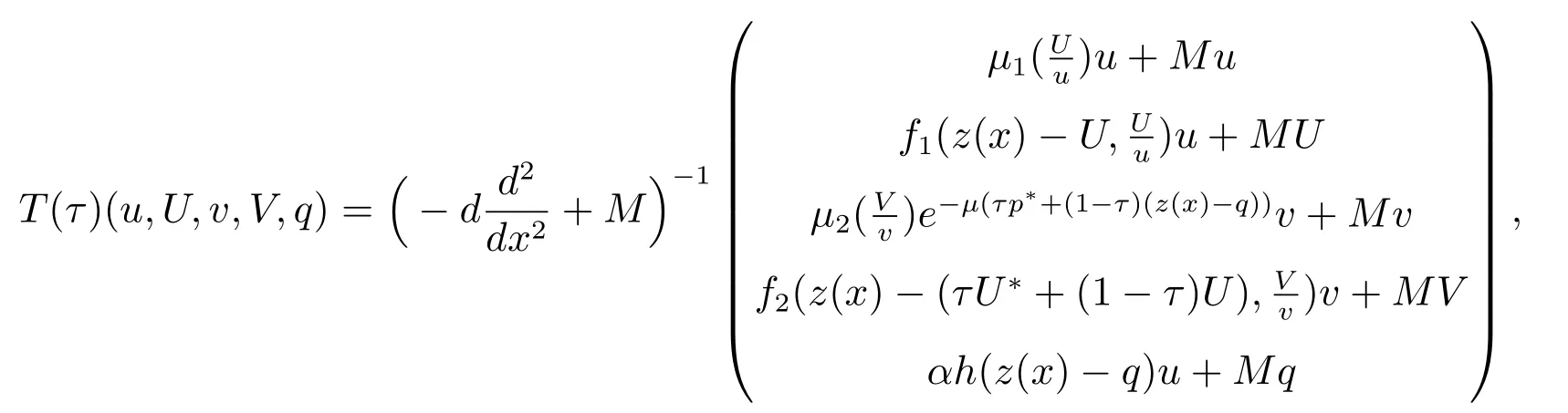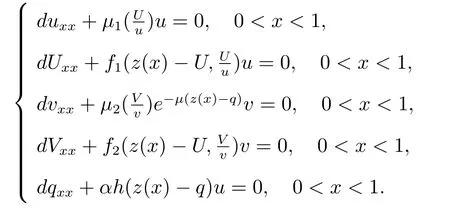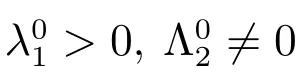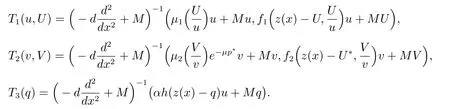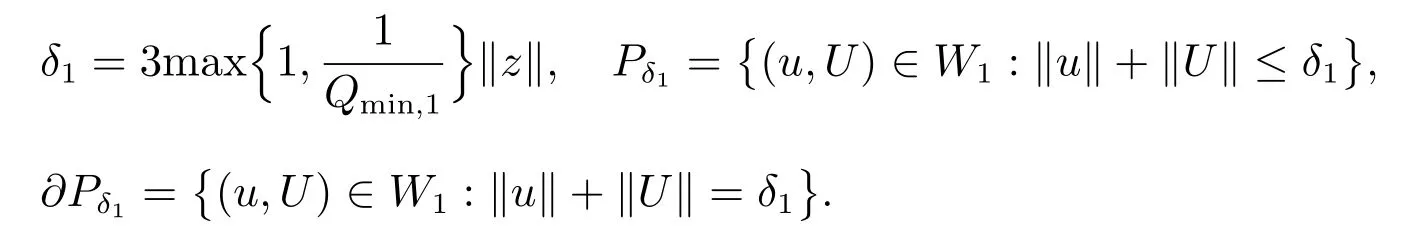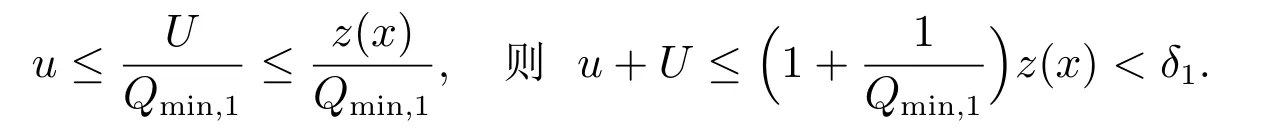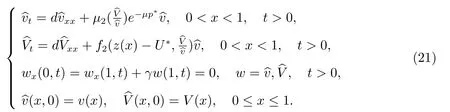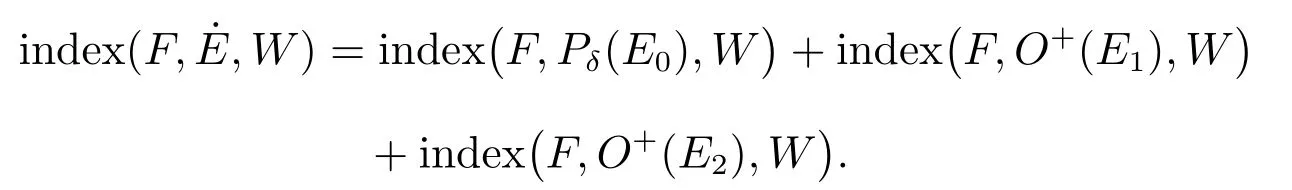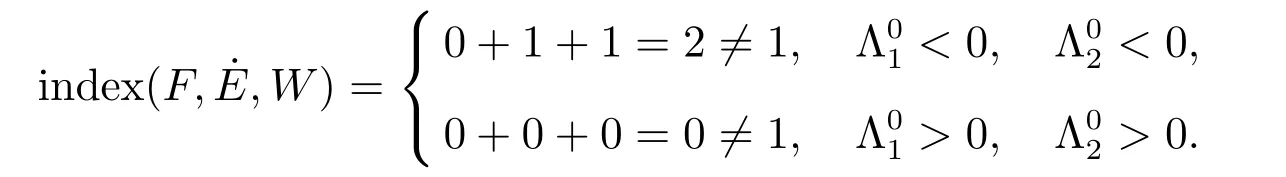一類具有內部存儲和外部抑制劑的非均勻恒化器模型
李雙妃, 王治國, 曹 毅
(陜西師范大學數學與信息科學學院,西安 710119)
1 引言
經典的恒化器模型通常假設營養吸收率與微生物的增長率成正比,因此被稱為常數產出模型.然而,Ketchum[1]在實驗中發現,在外部的營養物質耗盡后,藻類種群仍舊可以存活數周.這意味著,要恰當地描述生物的生長,應當將內部營養水平視為變量.因此,Droop[2,3]提出了帶有內部存儲的浮游植物生長模型.考慮到空間擴散的作用,Hsu 等[4,5]研究了一類帶有內部存儲的單資源非均勻恒化器模型.結果表明,存在臨界的擴散系數,當擴散系數小于臨界擴散系數時,將會出現競爭排斥或共存的現象;反之,兩物種均將死亡.Hsu 等[6]考慮了一類帶有內部存儲的消耗無機碳的雙資源非均勻恒化器模型,證明了物種存活時,正平衡解的唯一性及全局吸引性.
在生態學中,抑制劑可以降低某些有害生物的生長率,從而對環境治理具有重要作用.早在1986 年,Lenski 和Hattingh[7]提出了一類具有抑制劑的均勻恒化器模型.Hsu 和Waltman[8]研究了該模型解的一致持續性.Nie 和Wu[9]引入擴散,建立了具有擴散的非均勻恒化器模型,研究了系統的漸近動力學行為以及模型共存解的全局結構和局部穩定性.文獻[10]進一步研究了該模型正平衡解的唯一性和穩定性.然而,這些模型均忽略了物種對于營養的吸收存儲過程.
基于以上研究結果,本文研究一類具有內部存儲和外部抑制劑的恒化器模型.在t 時刻,假設營養物的濃度為S(t);種群密度為u(t), v(t);物種i 每個細胞所平均存儲的營養為Qi(t),其中i = 1,2 分別指代u 和v;抑制劑濃度為p(t).這里假設v 為受抑制劑影響的物種,u 為吸收抑制劑的物種.考慮如下均勻恒化器模型
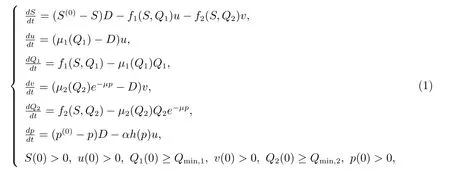
其中S(0)> 0 為營養物的輸入濃度,p(0)> 0 為抑制劑的輸入濃度,兩者均為常數;D 為稀釋率;μi(Qi)為物種i 的生長率;fi(S,Qi)為物種i 的營養吸收率;Qmin,i為物種i 的臨界細胞份額,即當細胞所存儲的營養低于該值時,物種將停止生長;α 為物種u 對抑制劑p 的吸收率;h(p) = p/(h1+p),其中h1為半飽和常數;函數e?μp為抑制劑p 對物種v 的抑制程度,其中μ>0 為常數.
文獻[3,11]中生長率μi(Qi)和吸收率fi(S,Qi)采取如下形式
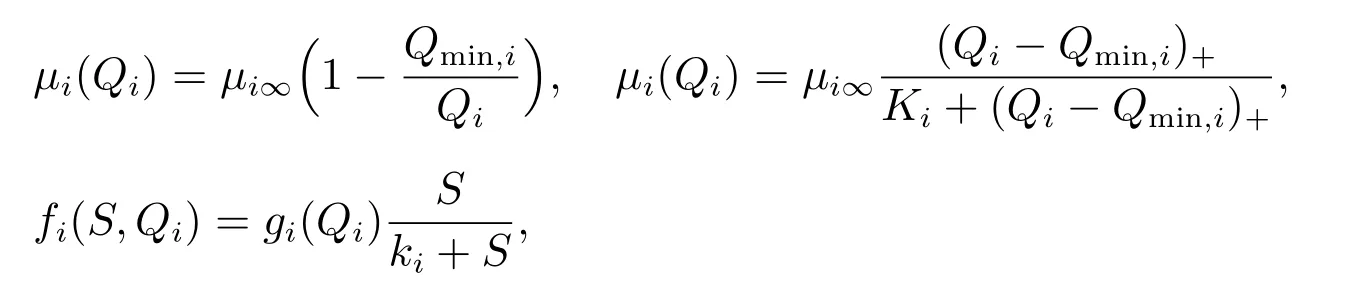
其中
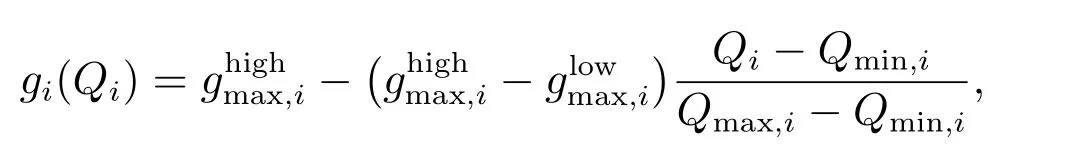
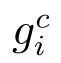
參考以上例子,對函數μi(Qi)和fi(S,Qi)作如下假設:
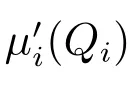
μi(Qmin,i)=0;
(H2):
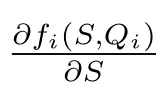
(ii) 當S ≥0, Qi≥Qmin,i時,
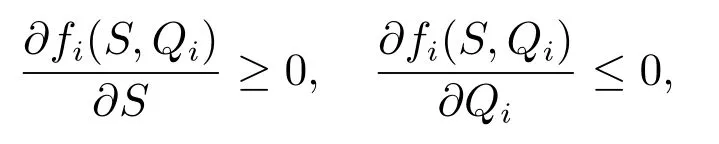
fi(S,Qi)≥0 幾乎處處成立;
(iii) 存在QBi∈(Qmin,i,+∞],對任意的(S,Qi) ∈{(S,Qi) ∈R+×[Qmin,i,+∞) :S >0, Qi∈[Qmin,i,QBi)},有
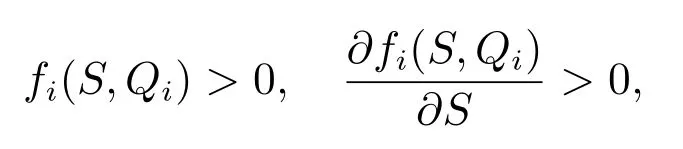
且當S = 0 或者Qi≥QBi時,fi(S,Qi) = 0.當QBi= +∞時,fi(S,Qi) = 0 當且僅當S =0.
令U = Q1u, V = Q2v 分別表示物種u, v 在t 時刻體內所存儲的營養.同時引入擴散,則系統(1)可化為
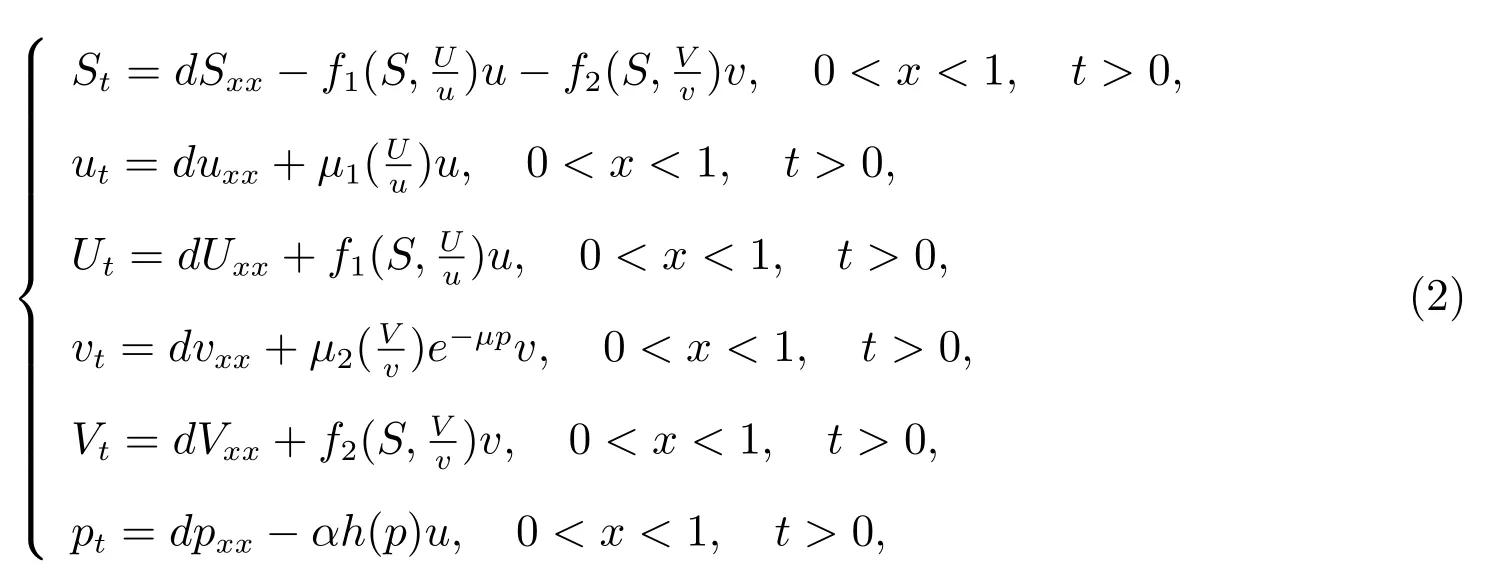
邊界條件和初始條件為
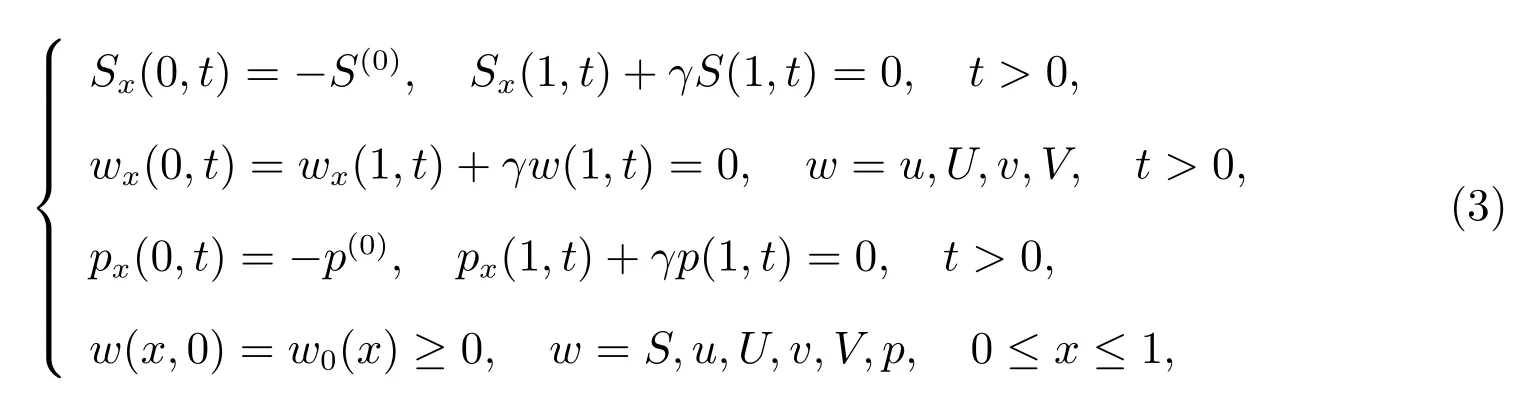
其中初始值函數u0(x), U0(x), v0(x), V0(x)滿足

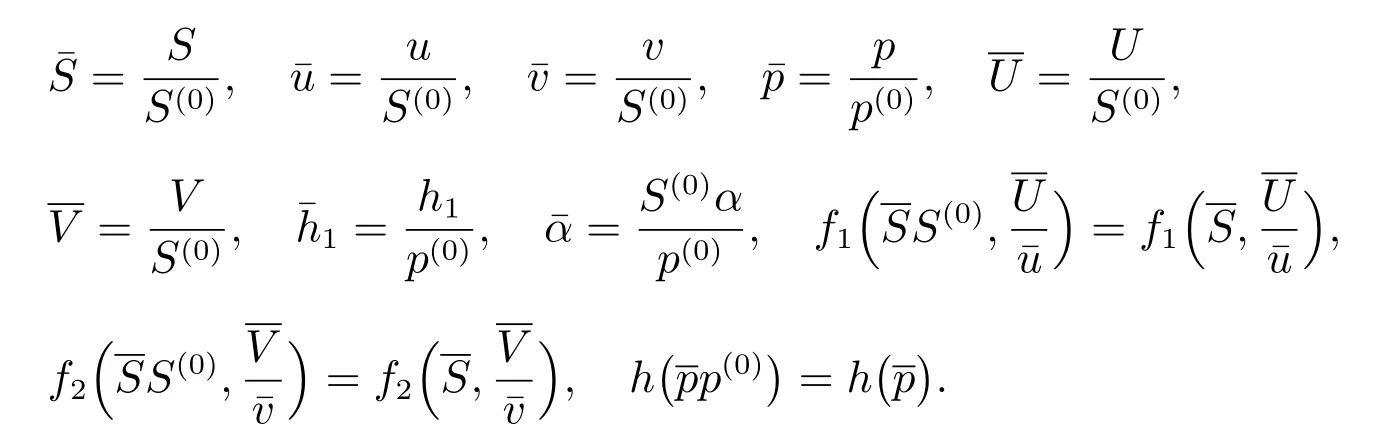
本文主要研究系統(2)–(3)正平衡解的存在性,故考慮相應的平衡態方程.令為節省記號,仍用原記號表示相應的無量綱化參數.因此,系統(2)–(3)可簡化為

邊界條件為
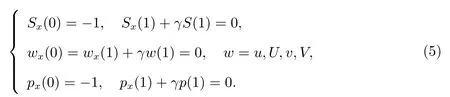
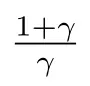
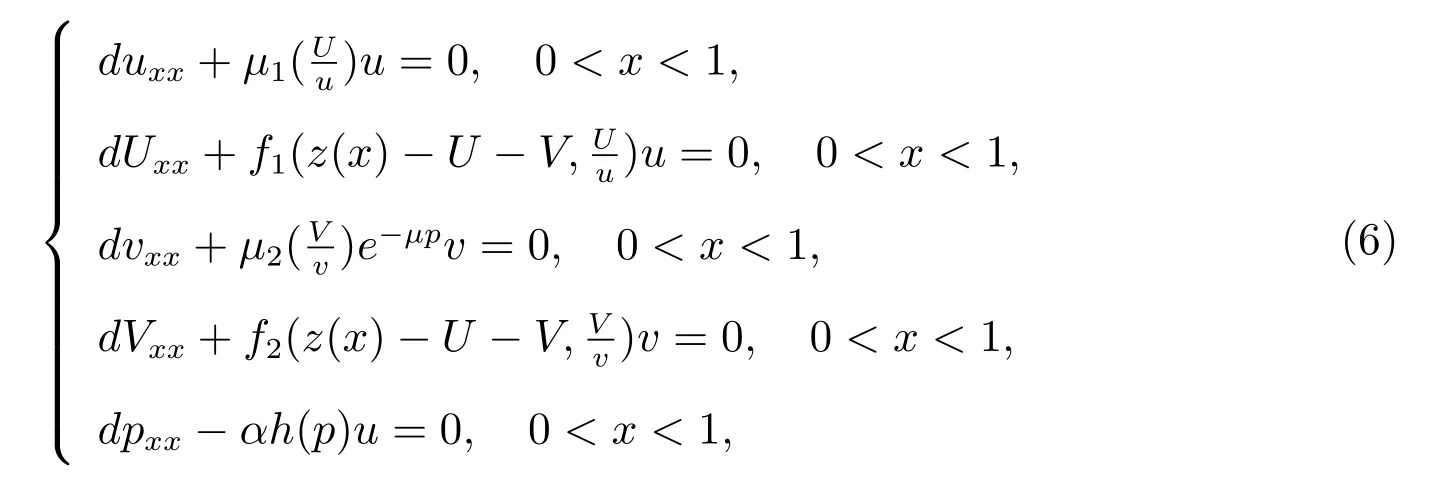
邊界條件為
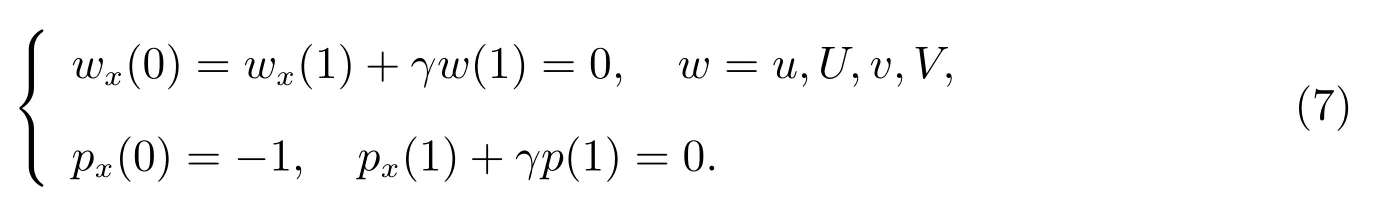
本文主要研究系統(6)–(7)正解的存在性,故對函數μi(Qi), fi(S,Qi)以及h(p)作如下延拓
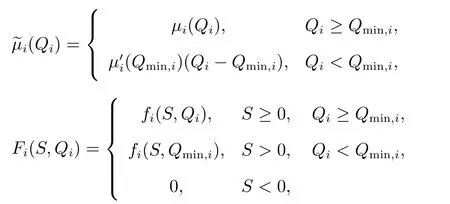
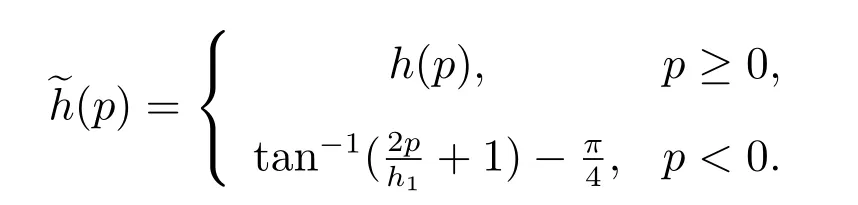
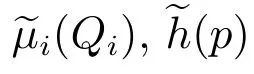
本文首先給出一些基本結果以及系統非負解的先驗估計,再利用Amann 的拓撲不動點指標理論計算算子在所有平凡和半平凡不動點鄰域內的指標,進而證明系統正平衡解的存在性.最后,需要指出的是在利用拓撲度理論研究系統正平衡解的存在性時,通常在系統各分量均非負的錐上使用拓撲度的不動點理論,如文獻[12,13],但這樣的錐對本文模型并不適用,本文將在更小的錐上使用不動點理論.
2 預備知識
首先考慮如下的非線性特征值問題
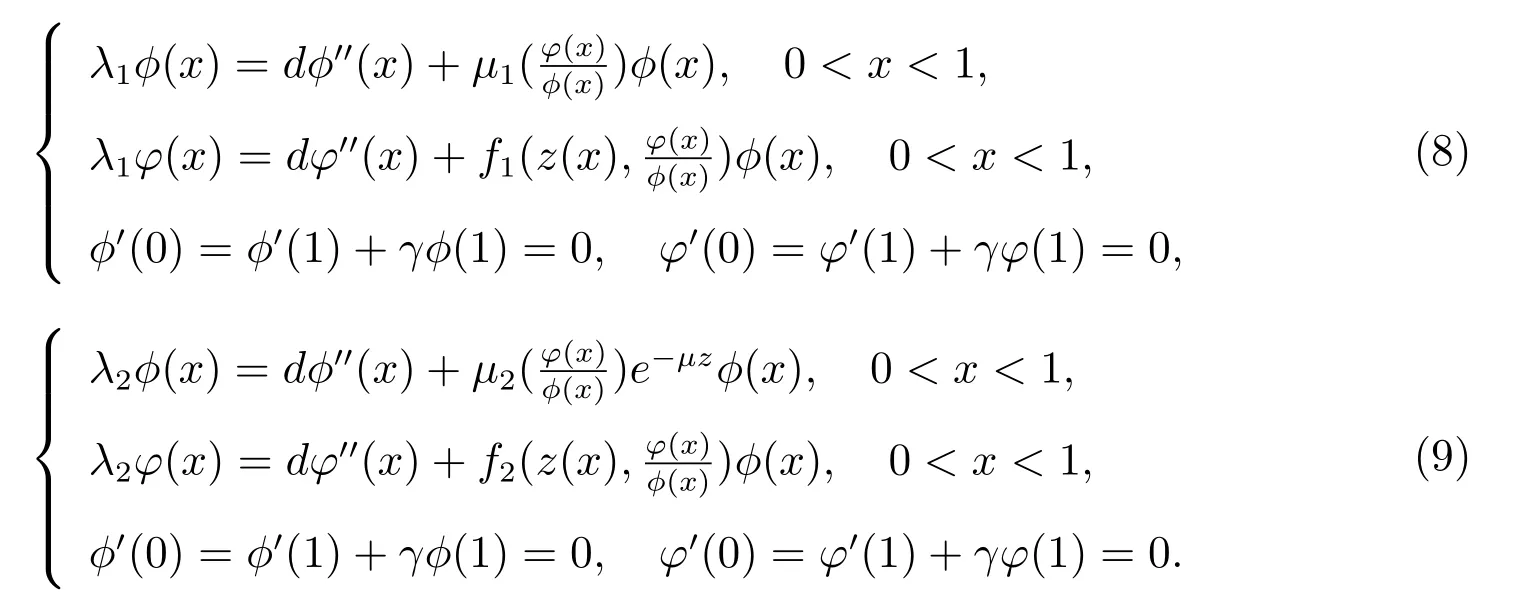

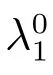
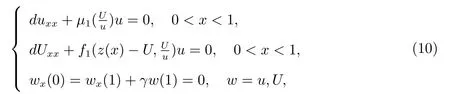
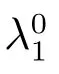
注:對于另一個單物種的平衡態問題
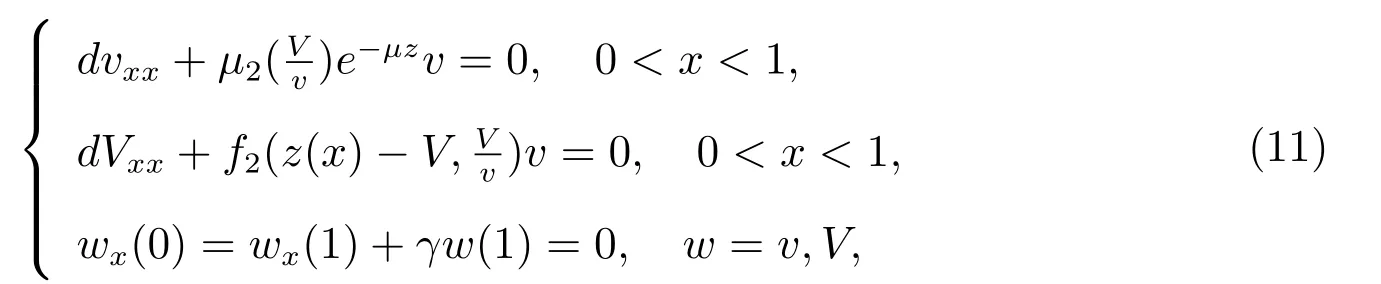
引理2[9]邊值問題

有唯一正解,記為p?,且滿足0 (i) u>0, v >0, U >0, V >0, 0 (ii) U +V (iii) U >uQmin,1, V >vQmin,2; 由文獻[6]得 其中 本節運用拓撲度理論研究系統(6)–(7)正解的存在性.令q = z(x) ?p,則p =z(x)?q.因此,系統(6)–(7)等價于 邊界條件為 引入以下空間 CB[0,1]={u ∈C[0,1]:ux(0)=ux(1)+γu(1)=0}, X =(C[0,1])5, W3={q ∈C[0,1]:q ≥0}, W =W1×W2×W3, E ={(u,U,v,V,q)∈W :∥u∥+∥U∥+∥v∥+∥V ∥+∥q∥≤R0, x ∈[0,1]}, ∥·∥為最大模范數. 定義F :E →X 如下 其中ξ1, ?1分別由(13),(14)給出 引理4對任意的λ ≥1, F(u,U,v,V,q) = λ(u,U,v,V,q)在W 中沒有解滿足∥u∥+∥U∥+∥v∥+∥V ∥+∥q∥=R0. 證明 假設(u,U,v,V,q)∈W 滿足F(u,U,v,V,q)=λ(u,U,v,V,q),且∥u∥+∥U∥+∥v∥+∥V ∥+∥q∥=R0,則有 故F(u,U,v,V,q)=λ(u,U,v,V,q)在W 中沒有解滿足 ∥u∥+∥U∥+∥v∥+∥V ∥+∥q∥=R0. 證明 由引理4 以及文獻[16]的引理12.1 可證得. Pδ(E0)={(u,U,v,V,q)∈W :∥u∥+∥U∥+∥v∥+∥V ∥+∥q∥≤δ}. 證明 對任意給定的充分小的?0,取0<δ <δ0?1,使得 記 因此,當(u,U,v,V,q) ∈Hδ+時,有∥u∥≤δz, ∥U∥≤δz, ∥v∥≤δz, ∥V ∥≤δz, ∥q∥≤δz.令ξ =2+γ ?γx2,則ξ >0, ?x ∈[0,1],且滿足ξxx<0, ξx(0)=ξx(1)+γξ(1)=0.易知(ξ,Qmin,1ξ,ξ,Qmin,2ξ,ξ)∈W.下面證明對任意的λ ≥0,方程 (u,U,v,V,q)?F(u,U,v,V,q)=λ(ξ,Qmin,1ξ,ξ,Qmin,2ξ,ξ) 為了證明系統正解的存在性,引入如下兩個非線性特征值問題 證明 (i)和(ii)的證明完全類似,這里僅給出(i)的證明.定義 則方程F(t)(u,U,v,V,q)=(u,U,v,V,q)滿足 以及邊界條件(16).若(u,U,v,V,q)是F(t)在?O+(E1)上的不動點,則u > 0, U >0, v ≥0, V ≥0, q > 0.由最大值原理必有v > 0, V > 0,否則(u,U,v,V,q) = E1,與(u,U,v,V,q)∈?O+(E1)矛盾,即u>0, U >0, v >0, V >0, q >0. 首先證明對任意的t ∈[0,1], F(t)在?O+(E1)上無不動點.假設(u,U,v,V,q) ∈?O+(E1)是F(t)的不動點,則u > 0, U > 0, v > 0, V > 0, q > 0.當t =0 時,F(0)(u,U,v,V,q)=(u,U,v,V,q)滿足 則q =q?=z(x)?p?.于是(v,V)滿足 index(F,O+(E1),W)=index(F(1),O+(E1),W)=index(F(0),O+(E1),W). 下面計算index(F(0),O+(E1),W).顯然,E1是F(0)在O+(E1)上唯一的不動點,因此index(F(0),O+(E1),W)=index(F(0),E1,W).對于τ ∈[0,1],定義 則T(τ)(u,U,v,V,q)=(u,U,v,V,q), τ ∈[0,1]具有邊界條件(16),且滿足 因此,由拓撲度的同倫不變性和不動點的乘積定理[17]得 index(F(0),E1,W)=index(T(0),E1,W)=index(T(1),E1,W) =index(T1,(u?,U?),W1)·index(T2,(0,0),W2)·index(T3,q?,W3). 現證index(T1,(u?,U?),W1)=1.令 對任意的λ ≥1, T1(u,U)=λ(u,U)滿足 且具有和(10)相同的邊界條件.類似引理4 可證,U ≤z(x).又 類似可證index(T3,q?,W3)=1. 假設對任意的λ ≥1,方程T2(v,V)=λ(v,V)在?O+(0,0)上存在解(v,V),則 且具有和(11)相同的邊界條件.由于λ ≥1,則(v,V)滿足如下微分不等式 因此(v,V)是如下拋物型問題的下解 另一方面,由于(v,V)∈?O+(0,0),故存在a1>0,使得 且具有和(11)相同的邊界條件.易證(v,V)是(21)的上解.同理,存在a2>0,使得 因此,當t →∞時,(v,V)≥(∞,∞),故對任意的λ ≥0,方程T2(v,V)=λ(v,V)在?O+(0,0)上無解.由[16]的引理12.1 得index(T2,(0,0),W2)=0. index(F,O+(E1),W)=index(T1,(u?,U?),W1)×index(T2,(0,0),W2)×index(T3,p?,W3)=1×1×1=1. index(F,O+(E1),W)=1×0×1=0. 由引理5 至引理7,可得 故假設不成立,即F 在˙E 至少有一個不動點.因此,系統(15)–(16)至少存在一個正解,即系統(6)–(7)至少存在一個正解.
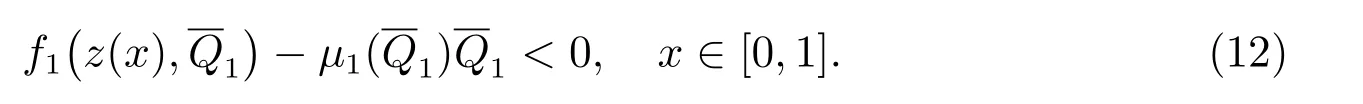
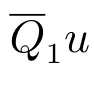
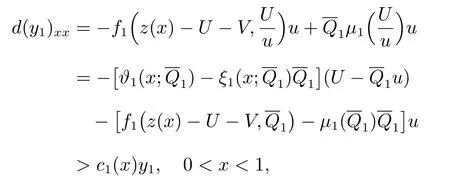
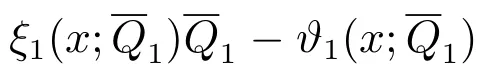
3 正解的存在性