基于改進PID算法的CFB鍋爐床溫控制

張靜 張瑞青

摘? 要：床溫是循環流化床鍋爐保持經濟、安全運行的重要參數，對床溫進行優化控制可以提高鍋爐運行的效率。針對床溫具有非線性、時變、多變量耦合的特點，常規PID控制已無法達到良好的控制要求，采用粒子群算法對PID進行改進，并在Matlab軟件平臺上仿真，結果表明，粒子群改進PID算法對床溫的控制效果比常規PID控制的穩定性、準確性、快速性更好。

關鍵詞：循環流化床鍋爐;床溫;PID算法;粒子群改進PID算法;Matlab仿真

中圖分類號： TP273? ? ? ? ? ? ? 文獻標志碼：A

循環流化床（Circulating fluidized bed， CFB）鍋爐具有對燃煤的利用率高、低污染以及負荷調節性能好的特點，因此得到了快速發展與廣泛應用[1]。床溫過高或者過低會直接影響CFB鍋爐的運行效率，所以必須將床溫控制在一定范圍內[2]。傳統PID控制算法對CFB床溫的控制效果已經滿足不了日益提高的控制要求，但是PID算法簡單、應用廣泛，所以研究改進PID算法對床溫進行控制具有重要的意義。

1 粒子群改進PID算法

粒子群算法是模仿鳥類捕食的過程：若干只鳥在一定區域內尋找食物，每只鳥都知道整個鳥群目前所搜索的所有位置，根據這些位置，鳥類自行判斷改變自己的搜索方向，經過一定時間的搜索后，小鳥會距離食物越來越近，最終找到食物的位置。每只鳥即為粒子。在鳥類捕食的過程中，鳥類會自行判斷自身位置相對于食物位置的優劣性來決定自身的飛行方向，而在粒子群算法中，用適應度函數來衡量粒子位置的優劣性，根據適應度函數值粒子決定自身位置的變化方向，向當前的最優解運動[3]。

粒子群尋優步驟是：首先初始化粒子群，將粒子隨機分布在搜索空間內，根據適應度函數計算每個粒子的適應值，即個體極值，通過個體極值的對比，找出當前所有粒子的最優解，即全局極值。所有的粒子都會向全局極值的位置運動，在運動的過程中，個體極值和全局極值會不斷變化，粒子的運動也隨之不斷地變化，在一定時間后，所有的粒子都會聚集在某一個點的附近，這個點就是所尋找的最優解[4]。

PID控制器參數的優化問題，即取得kp，ki，kd? 3個參數的最優值，使控制系統的控制效果達到最佳。適應度函數是評價粒子群粒子好壞的重要標準，選取不同的適應度函數會直接影響系統優化的最優解，時間誤差絕對值積分在PID控制系統的性能評價指標里是使用最普遍的一種，不但可以減少誤差對輸出響應的影響，而且可以使偏差調節作用增加，具有結構簡單、震蕩幅度適中等特點，所以選取時間誤差絕對值積分作為粒子群算法的適應度函數[5]。

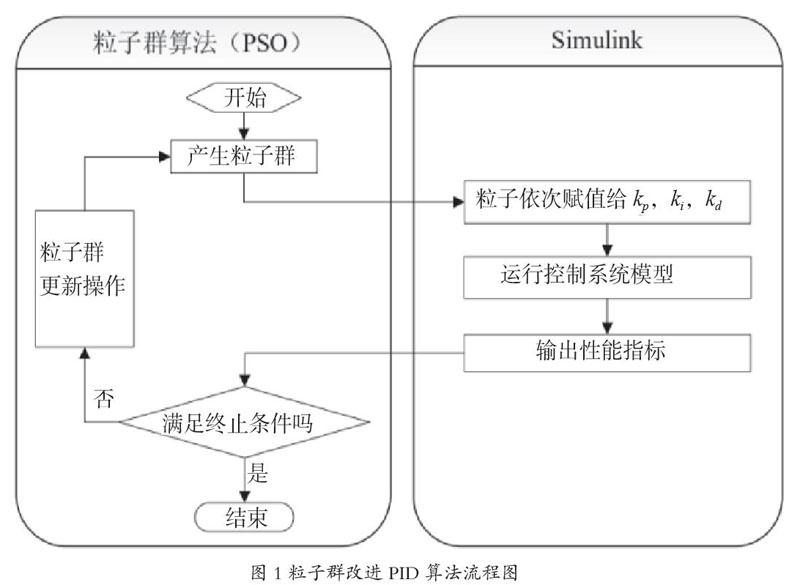
基于粒子群算法優化PID參數的流程：首先，粒子群初始化，產生隨機粒子，然后將隨機粒子的值賦予PID控制器的kp，ki，kd? 3個參數，針對該參數使系統模型運轉，得到此時的適應度函數值，將該值作為輸出，輸入判斷模塊，如果不滿足終止條件，則粒子群進行更新，再次賦予PID的3個參數進行運算，如果滿足終止條件，則退出循環輸出最優值。粒子群改進PID算法流程圖如圖1所示。

2 CFB機組床溫控制

2.1 PID床溫控制

傳統PID控制器的結構層次和控制原理相對簡單，實現難度低，可用于多種被控對象、多樣的控制環境，所以，傳統的PID控制器普遍地應用于CFB鍋爐的控制系統中。

CFB機組PID床溫控制系統為單回路控制系統，采用調節給煤量來調節CFB床溫，工作原理如圖2所示，R 是床溫的設定值，Y 是床溫的測量值，用溫度變送器采集床溫的數值送入調節器，形成一個單回路控制策略。

給煤量與床溫之間的影響關系用傳遞函數來表示：

式中：s代表t時間域映射到復數域中的復數變量，G（s）為傳遞函數，即床溫的復數域模型。

在MATLAB的Simulink仿真軟件中搭建PID單回路控制系統，主要用到的仿真模塊有階躍信號模塊、PID控制器模塊、傳遞函數模塊、延遲模塊以及示波器模塊，進行連接后仿真。

PID參數整定方法利用臨界比例帶法，先將系統置于單純比例控制的條件下，通過仿真得到系統的臨界比例帶和臨界震蕩周期，然后再根據經驗公式求出PID控制器的各參數值，最后再調整各個參數達到良好的控制效果。通過對PID參數的整定，PID參數設置為kp=1.205，ki? =0.005，kd=2.34。PID床溫系統的仿真曲線如圖3所示，橫坐標范圍為0 s～300 s，每格代表50 s;縱坐標范圍為0 ℃～1.5℃，每格代表0.5℃。從圖中可得：系統超調量為42.3%，上升時間為46 s，調節時間為210 s。

2.2 粒子群改進PID床溫控制

在粒子群算法算法中，設置群體規模為10，，最大迭代次數為100。通過粒子群算法對PID的kp，ki，kd? 尋優，將尋優找到的最優值kp=1.042、ki=0.001、kd =4，代入PID控制器，系統響應曲線如圖4所示，橫坐標范圍為0 s～300 s，每格代表50 s;縱坐標范圍為0℃～1.2℃，每格代表0.2 ℃。從圖4中可得：系統的超調量為16.7%，上升時間為44 s，調節時間為135 s。

對比圖3與圖4仿真控制系統曲線，粒子群改進PID算法后的控制系統超調量從改進前的42.3%下降到16.7%，控制系統更平穩、無大的波動，生產過程更平穩;上升時間由改進前的46 s下降到44 s，控制系統反應更快，快速性得到提高;調節時間由改進前的210 s縮短到135 s，說明系統在受到階躍信號作用后能更快速地過渡到穩定狀態。

3 結論

針對傳統PID算法無法滿足當今CFB床溫控制要求，該文設計粒子群改進PID算法的床溫控制系統，通過Matlab仿真得出：粒子群改進PID算法的床溫控制響應曲線與傳統PID控制床溫的響應曲線相比較，系統的超調量減小，系統更平穩，調節時間縮短，系統能更快的達到穩定狀態。

參考文獻

[1]鄭守忠，張勇.循環流化床鍋爐床溫影響因素的試驗研究[J].熱力發電，2007（9）：36-38.

[2]陳亮.循環流化床鍋爐床溫控制系統的應用研究[D].北京：華北電力大學，2013.

[3]謝曉鋒，張文俊，楊之廉.微粒群算法綜述[J].控制與決策，2003， 18（2）： 129-134.

[4]楊智，陳穎.改進粒子群算法及其在PID整定中的應用[J].控制工程，2016（2）：161-166.

[5]吳垚，霍亮生，黎進遠，等.自適應混沌粒子群算法及在PID整定中的應用[J].計算機仿真， 2014（8）：377-381.