函數奇偶性的判定方法
◇ 山東 師吉芹
函數的奇偶性反映了函數圖象的對稱性,充分體現了“數”與“形”可以互相轉化的思維.數形結合是進行數學分析和數學研究的有力工具,對函數部分的知識體系和綜合應用具有紐帶的作用,而正確快速判斷函數的奇偶性是解決問題的關鍵所在.
1 定義法
利用函數奇偶性的定義進行判別時,要注意以下兩點:
1)在整個函數的定義域內考慮;
2)具有奇偶性的函數,其定義域一定關于原點對稱.

分析應該先求出函數f(x)的定義域,再對相應的解析式加以恒等變換后,利用定義判斷奇偶性.
解函數f(x)的定義域為

即x2-4=0,解得x=±2,所以f(x)的定義域為{2,-2},原函數可以恒等變形為f(x)=0(x=±2),此時f(-x)=f(x)與f(-x)=-f(x)同時成立,所以函數既是奇函數又是偶函數.
2 圖象法
根據具有奇偶性的函數的圖象特征,函數是奇(偶)函數的充要條件是它的圖象關于原點(y 軸)對稱.
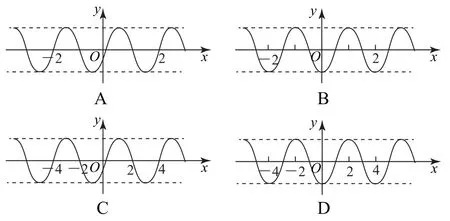
分析結合題目中給出的關系式確定函數所具有的奇偶性,再結合各選項中函數的圖象確定各自相應的奇偶性進行綜合判定.
解由f(-x)=f(x),可知函數f(x)為偶函數,其圖象關于y 軸對稱,可以排除選項A 和C.
再利用f(x+2)=f(x),可知函數為周期函數,且T=2,必滿足f(4)=f(2),可以排除選項D.故選B.
3 性質法
在各自函數公共定義域的條件下,偶函數與偶函數的和、差、積、商(分母不為零)仍為偶函數;奇函數與奇函數的和、差仍為奇函數;奇(偶)數個奇函數的積、商(分母不為零)為奇(偶)函數;一個奇函數與一個偶函數的積為奇函數.
A.f(x)g(x)是偶函數
B.|f(x)|g(x)是奇函數
C.f(x)|g(x)|是奇函數
D.|f(x)g(x)|是奇函數
分析結合函數的奇偶性所滿足的關系式,根據奇偶性的定義,通過函數奇偶性的性質,利用排除法加以分析與判定.
解因為f(x)是奇函數,g(x)是偶函數,所以有f(-x)=-f(x),g(-x)=g(x),于是f(-x)·g(-x)=-f(x)g(x),即f(x)g(x)為奇函數,選項A 錯誤.
|f(-x)|g(-x)=|f(x)|g(x),即|f(x)|·g(x)為偶函數,選項B錯誤.
f(-x)|g(-x)|=-f(x)|g(x)|,即f(x)·|g(x)|為奇函數,選項C正確.
|f(-x)g(-x)|=|f(x)g(x)|,即f(x)·g(x)為偶函數,選項D 錯誤.
綜上,故選C.
4 特殊變形法
對于抽象函數奇偶性的判斷與證明問題,往往要對相應關系式進行變形,代入特殊值,以創新的角度結合函數奇偶性的定義來判斷與證明相應函數的奇偶性問題.
分析可根據函數奇偶性的定義進行證明,應由條件先得到f(0)=0后,再利用條件f(x1+x2)=f(x1)+f(x2)中x1,x2的任意性加以變形,從而使結論得證.
證明對任意x,y∈R均有f(x+y)=f(x)+f(y),若令x=y=0,則f(0)=f(0)+f(0),f(0)=0,再令y=-x,則可得f(0)=f(x)+f(-x),因為f(0)=0,所以f(-x)=-f(x),故f(x)是奇函數.
實際判斷函數的奇偶性問題時,有時可單獨使用其中的一種方法來處理,有時要用多種方法來綜合處理.

