平行線分線段成比例定理的三類應用

◇ 山東 王德康

平行線分線段成比例定理是三角形相似問題的進一步拓展,也為證明三角形內角平分線定理提供了依據,在考查中也常常獨立作為考題出現.下面我們就結合實例,來看一看平行線分線段成比例定理的三類典型應用問題.

1 長度求解問題

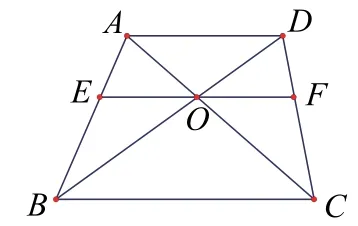
圖1

2 線段相等問題

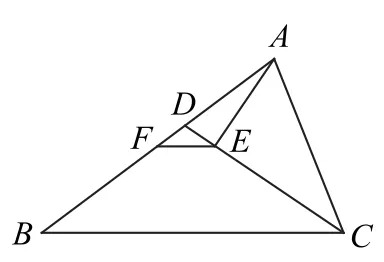
圖2

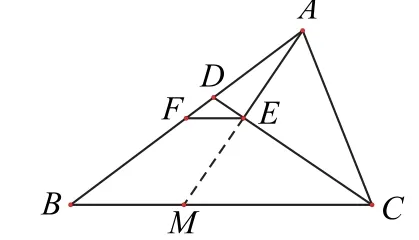
圖3

3 直線平行問題

圖4

證法1如圖5,延長AD至G,使DG＝MD,連接BG,CG,因 為BD ＝DC,MD ＝DG,所以四邊形BGCM 為平行四邊形,所以EC∥BG,FB∥CG,所以,所以,所以EF∥BC.

圖5

圖6

證法2如圖6,過A 作BC的平行線,與BF,CE 的延長線分別交于G,H,因為AH ∥DC,AG∥BD,所以,所以,因為D 是BC中點,所以BD ＝DC,故AH ＝AG,因為HG∥BC,所以,又因為AH ＝AG,所以,所以EF∥BC.

在利用平行線分線段成比例定理解決實際問題時,往往需要借助一對中間比來達到解決問題的目的.因此我們應注意找到平面幾何圖形中的點與線的位置關系,合理、正確地添加相應的輔助線,構造對應的中間比,使問題找到通路,從而快速地解決.