芻議高階思維視域下簡便運算的教學策略

沈君

摘要：思維培育是數(shù)學教育的重要任務。文章以簡便運算的教學為例，嘗試以錯題解讀為切入點，思考數(shù)學教育的旨歸，從教材解讀、多元表征、辨析討論、開放練習等角度探尋培養(yǎng)學生高階思維能力的教學策略。

關鍵詞：小學數(shù)學 高階思維 簡便運算

簡便運算是計算教學中的重要組成部分。它建立在四則運算的基礎上，要求學生運用運算律，根據(jù)算理簡化較復雜的運算，提高速度和正確率。實際應用中，由于簡便運算類型多樣，變式復雜，許多學生運算時往往不知所措、錯誤頻出。因此，厘清教育發(fā)展定位，變革陳舊教學模式，在知識傳授的同時進行高階思維培育，是改變現(xiàn)狀的有效途徑。

一、錯題分析，初窺學生思維現(xiàn)狀

簡便運算是計算策略化和最優(yōu)化的綜合，也是學生思維能力的綜合體現(xiàn)。從學生簡便運算中部分錯題情況來分析學生的思維狀態(tài)，以反思教學方式不足。

錯例1：42÷（7+7）

題型分析：在本題中，常有學生把乘法分配律與之混淆，用42分別除以兩個7，強行簡算。這個題目錯誤率在高年級較中年級更高，主要是學生在了解乘除互逆運算后，將之與頭腦中的乘法分配律進行混淆造成。

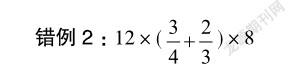
題型分析：有部分學生將括號內(nèi)先通分再展開計算，還有部分學生注意到可使用乘法分配律，卻忽視了乘8。這說明部分學生缺乏整體思維，只發(fā)現(xiàn)該題有部分乘法分配律的呈現(xiàn)，而沒有注意到題目的本質是三部分相乘，將本題視作新類型束手無策。

學生的種種錯誤，折射出其思維訓練的不足。真實的數(shù)學情境往往狀態(tài)新奇、多條件并存，學生需要運用已知的信息分析、綜合和評價，多法并舉才能解決。

二、立足學生發(fā)展，思考數(shù)學教學旨歸

高階思維就是指發(fā)生在較高認知水平層面上的心智活動或認知能力。它是建構高階能力的核心，是提出問題能力、批判性思維能力、反思質疑能力和創(chuàng)新能力生發(fā)的源泉，是促使兒童數(shù)學向上生長的重要力量。

陶行知先生曾提出“要以學生的發(fā)展為本”。數(shù)學教育不應僅停留于傳授基本知識與基本技能的較淺層面，而應著眼于適應社會和學生的終身發(fā)展。在教學中，教師應關注數(shù)學思維的培育，精心設計活動，讓學生能在真實的數(shù)學模型中闡釋觀點、交流方法、感悟意義、優(yōu)化方法，提升高階思維發(fā)展。

三、高階思維視域下簡便運算的教學策略

在課堂教學中，教師應站在思維培育的角度，調(diào)整教學的策略，在教學中恰當?shù)靥幚斫滩摹⒈碚鳌⒈嫖觥⒕毩曋g的關系，把握教學本質，提高思維培育質量。下面僅以簡便運算中乘法結合律的教學為例，淺議高階思維視域下簡便運算的教學策略。

1.三維讀教材，把握教育任務

事實上，學生在學習運算律之前，早已不知不覺地用上了這些規(guī)律。例如，二年級計算進位加法24+8：24+6=30，30+2=32。這里就運用了加法結合律。簡便運算教學的真正教育目的不僅是掌握運算律的表達形式及應用運算律進行簡便計算，而是讓學生在經(jīng)歷歸納、抽象、辨析與質疑的過程中，自然生發(fā)高階思維，從而在現(xiàn)實生活中自然地進行運用。把教材中顯性的知識要點、隱性的教育任務與實用的數(shù)學價值結合在一起，就構成了解讀教材的三維視圖。

2.多元化表征，激活思維

曹培英教授曾說過，小學數(shù)學的核心問題是適度抽象，謀求兒童思維的形象性與數(shù)學的抽象性的協(xié)調(diào)統(tǒng)一。因此，教師在教學中可以通過多元表征的方式幫助學生理解知識，讓算理說得通、看得見、悟得透。

（1）言語表征

教學時，教師可以讓學生用自己的話來說說乘法結合律的意思。有的學生會直接用字母表達式，即（a×b）×c=a×（b×c）。這時，教師可以進一步啟發(fā)，如果把a 、b、c看作三個乘數(shù)，那么這個表達式是什么意思？學生可以說出：三個乘數(shù)相乘，可以先把前兩個乘數(shù)相乘，也可以先把后兩個數(shù)相乘，結果不變。這樣，學生不僅能在認知上理解規(guī)律，而且能夠通過語言進行表達。

（2）圖形表征

將抽象的數(shù)學運算與形象、直觀的圖形進行相互轉化，是讓學生理解算理、遷移算法的有效路徑。在乘法結合律的教學中，教師可以用數(shù)字舉例，以3×2×4 配點子圖，可以先橫著看，得到3×2，再一行一行地往下數(shù)，就可以得到3×2×4；也可以先豎著數(shù)，發(fā)現(xiàn)左邊有3×4個點子，再往右發(fā)現(xiàn)有這樣的兩部分，進而得到3×2×4；還可以把3個點子當作一個整體，先數(shù)一數(shù)一共有幾個3，發(fā)現(xiàn)一共有2×4個，然后得到結果3×2×4。

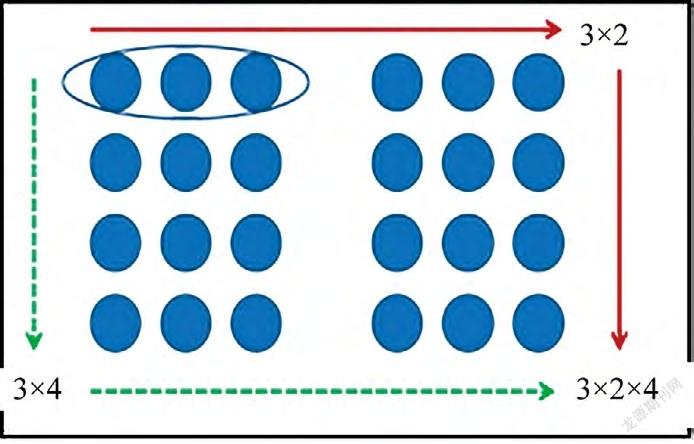
在教學中，教師借助圖形使學生明白了算理的內(nèi)在本質。數(shù)與形的相互輔助，讓學生實現(xiàn)了認知上的飛躍，完成了抽象到具象之間的轉化，實現(xiàn)了思維的可視化。

（3）符號表征

教學中，教師可以讓學生再列舉一些這樣的算式。通過觀察、計算、比較，學生提出這些算式的結果都是相等的。在此基礎上，教師可以讓學生用自己喜歡的方式來表達這樣的算式。有的學生會采用圓圈、方塊、三角來組成算式；有的學生會用甲、乙、丙表示三個數(shù)合成算式，還有的學生則嘗試用不同的字母來表達式子間的關系。這樣的操作活動，不僅使學生經(jīng)歷了不完全歸納的過程，更讓學生的思維水平由表象水平上升到抽象水平。

3.辨析大討論，促進思維發(fā)展

《義務教育數(shù)學課程標準（2011版）》指出，“要尋求合理簡潔的運算途徑解決問題”。例如，在教學540÷36 時，學生可能會出現(xiàn)540÷4÷9、540÷9÷4、540÷6÷6、540÷2÷18、540÷18÷2等多種解法。教師通過引導學生觀察、交流，讓學生自發(fā)產(chǎn)生思考、辨析、質疑與評價。交流中，學生發(fā)現(xiàn)第一種和最后一種的第一步540÷4和540÷18都要通過筆算；540÷2個別學生易誤算。在對比中，學生自主選擇了最易計算、最不容易出錯的解法。在個體或群體為了做出決定而進行的分析、交流、判斷與選擇的過程中，學生形成了深刻、理性的認知，同時促使思維邁向高階發(fā)展。

4.創(chuàng)意微練習，豐盈高階思維

教學的本質是知識的再創(chuàng)造。教師要為學生參與數(shù)學活動提供足夠的時間和空間，讓學生有條件、有機會去觀察、嘗試、思考、討論，促使學生將經(jīng)過自己的親力親為轉化為知識的再生成、再創(chuàng)造。

例如，在教學簡便運算時，教師讓學生用自己喜歡的方法計算25×44。有的學生用25×4×11，有的用25×40+25×4，有的交換乘數(shù)位置，用44×5×5計算，還有的學生列式44×100÷4。由最后一種解法，部分學生甚至聯(lián)想到44×5×10÷2。學生的運算方法沒有依靠教師現(xiàn)成的說教，而是創(chuàng)造性地大量生成。多角度、多策略思考問題，創(chuàng)造性地解決問題，這正是高階思維追求的靈活品質。

綜上所述，思維培育是數(shù)學教育的重要任務。教師應當在理解教材的基礎上，采用多元的通道，引導學生在學習中進行表征、辨析和創(chuàng)造，發(fā)展高階思維的能力，賦予兒童數(shù)學向上生長的力量。

參考文獻

[1]馮貴群.言語與符號：培育學生思維的重要表征[J].教學與管理，2019（07）：34.

[2]趙瑞生.在算術運算的教學中培養(yǎng)學生的準變量思維[ J].江蘇教育，2013（33）：11.

[3]孔凡哲，史寧中.中國學生發(fā)展的數(shù)學核心素養(yǎng)概念界定及養(yǎng)成途徑[ J].教育科學研究，2017（06）：5-11.