以課為背景的試題解析

劉頓

在近幾年的中考試題中，以數(shù)學(xué)活動(dòng)課或數(shù)學(xué)興趣小組的課外活動(dòng)等模式為背景的試題，逐漸成為命題的一種新趨勢(shì). 為方便同學(xué)們及時(shí)了解此類試題在中考中的動(dòng)態(tài)，現(xiàn)選兩例供參考！

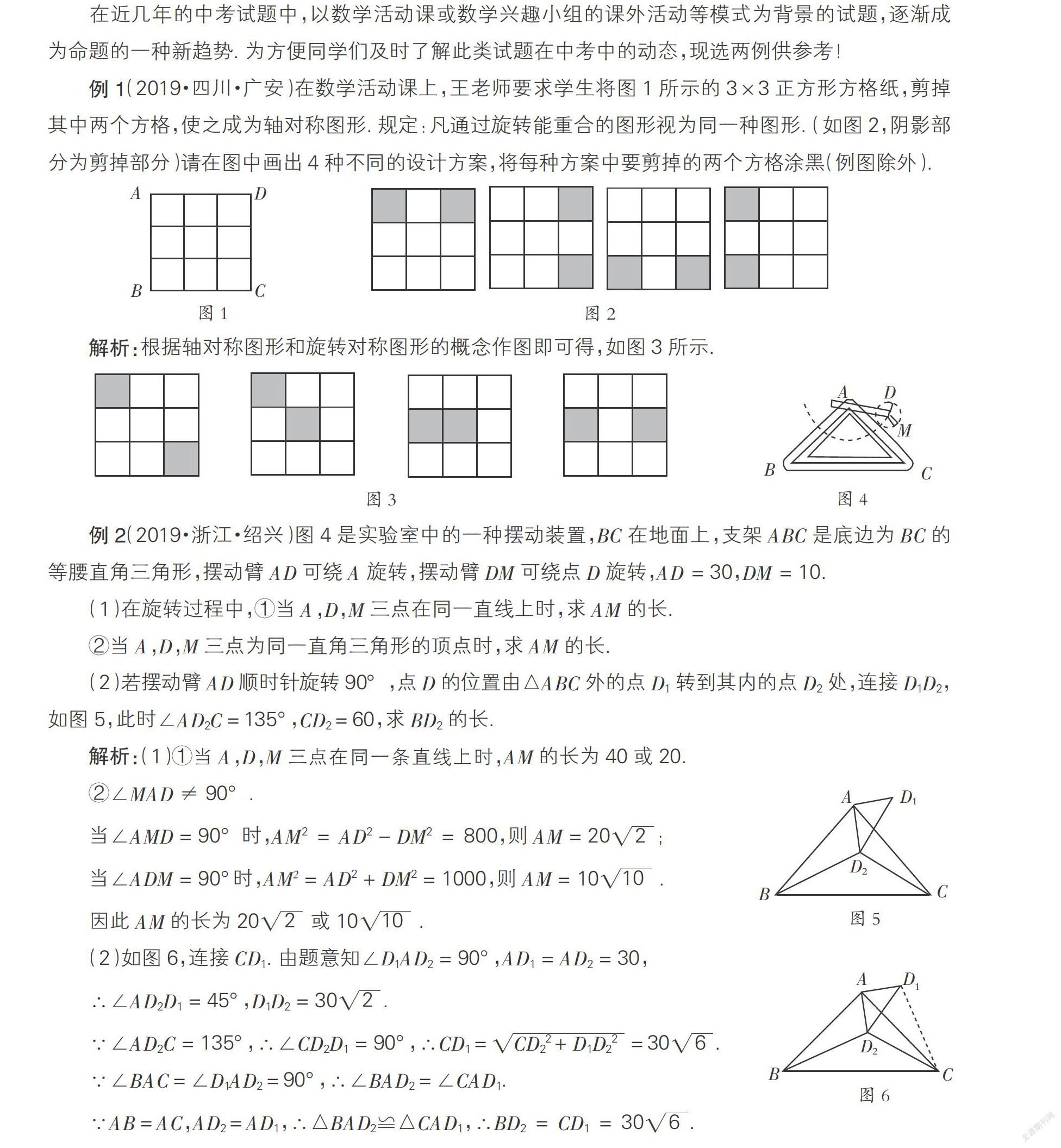
例1（2019·四川·廣安）在數(shù)學(xué)活動(dòng)課上，王老師要求學(xué)生將圖1所示的3×3正方形方格紙，剪掉其中兩個(gè)方格，使之成為軸對(duì)稱圖形. 規(guī)定：凡通過旋轉(zhuǎn)能重合的圖形視為同一種圖形. （如圖2，陰影部分為剪掉部分）請(qǐng)?jiān)趫D中畫出4種不同的設(shè)計(jì)方案，將每種方案中要剪掉的兩個(gè)方格涂黑（例圖除外）.

解析：根據(jù)軸對(duì)稱圖形和旋轉(zhuǎn)對(duì)稱圖形的概念作圖即可得，如圖3所示.

例2（2019·浙江·紹興）圖4是實(shí)驗(yàn)室中的一種擺動(dòng)裝置，BC在地面上，支架ABC是底邊為BC的等腰直角三角形，擺動(dòng)臂AD可繞A旋轉(zhuǎn)，擺動(dòng)臂DM可繞點(diǎn)D旋轉(zhuǎn)，AD = 30，DM = 10.

（1）在旋轉(zhuǎn)過程中，①當(dāng)A，D，M三點(diǎn)在同一直線上時(shí)，求AM的長(zhǎng).

②當(dāng)A，D，M三點(diǎn)為同一直角三角形的頂點(diǎn)時(shí)，求AM的長(zhǎng).

（2）若擺動(dòng)臂AD順時(shí)針旋轉(zhuǎn)90°，點(diǎn)D的位置由△ABC外的點(diǎn)D1轉(zhuǎn)到其內(nèi)的點(diǎn)D2處，連接D1D2，如圖5，此時(shí)∠AD2C=135°，CD2=60，求BD2的長(zhǎng).

解析：（1）①當(dāng)A，D，M三點(diǎn)在同一條直線上時(shí)，AM的長(zhǎng)為40或20.

②∠MAD ≠ 90°.

當(dāng)∠AMD = 90°時(shí)，AM2 = AD2 - DM2 = 800，則AM = 20;

當(dāng)∠ADM = 90°時(shí)，AM2 = AD2 + DM2 = 1000，則AM = 10?.

因此AM的長(zhǎng)為20或10?.

（2）如圖6，連接CD1. 由題意知∠D1AD2 = 90°，AD1 = AD2 = 30，

∴∠AD2D1 = 45°，D1D2 = 30.

∵∠AD2C = 135°，∴∠CD2D1 = 90°，∴CD1==3.

∵∠BAC=∠D1AD2=90°，∴∠BAD2=∠CAD1.

∵AB=AC，AD2=AD1，∴△BAD2≌△CAD1，∴BD2 = CD1 = 30.