構建反比例數模 把握物理量關系
周雪夏





摘 要:物理學中很多物理量之間的變化是反比例關系,分析解決物理問題要充分運用反比例知識.從物理問題抽象出數學函數模型,利用數據或圖像的方法理解函數關系,從而尋找到物理量之間的反比例關系.
關鍵詞:物理量;反比例;函數模型;數據圖像
中圖分類號:G632? ? ? 文獻標識碼:A? ? ? 文章編號:1008-0333(2020)23-0048-02
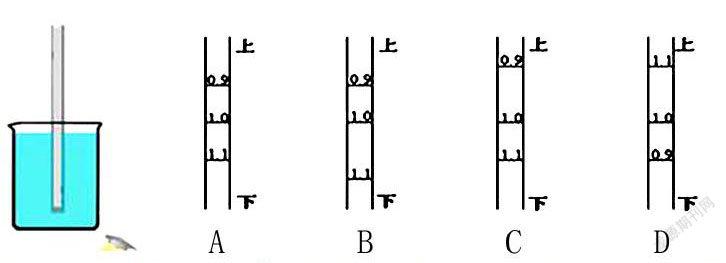
例題 利用一根吸管制作一個簡易密度計.
(1)為了讓飲料吸管能豎直的漂浮在液體中,應在吸管的(上端/下端)塞入一些銅絲作為配重,并用石蠟將吸管的下端封閉起來.若將它放入液體中后不能豎直漂浮,請提出改進做法.
(2)這根吸管豎直漂浮在不同液體中時,液體的密度越大,它露出液面部分的長度(越長/越短/不變),受到的浮力大小(變大/變小/不變)
(3)通過正確計算,在吸管上標出對應的刻度線,便制成了一個簡易的吸管密度計.下列四種刻度的標示合理的是( )
本題(3)的難點是數學知識反比例關系在物理中的應用.下面就反比例關系的教學談一下我的做法.
一、構建數學模型,加深函數關系的印象
1.關系公式化
兩個相關聯的量,一個量變化(增大或縮小),另一個量也隨著變化(縮小或增大),并且這兩個量相對應的兩個數的乘積一定,則這兩個量就叫做成反比例的量,它們的關系叫做反比例關系.如果用字母x和y表示兩個相關聯的量,用k表示它們的積,反比例關系可以用下面函數關系式表示:xy=k(k為常數,k≠0,x≠0,y≠0).
2.圖像印象法
反比例函數xy=k (k為常數,k≠0,x≠0,y≠0),x的取值范圍是不等于0的一切實數,且y也不能等于0.其圖像是由以原點為對稱中心的兩支曲線組成,稱它們為雙曲線.這兩支曲線都與x軸、y軸不相交.k>0時,圖像在一、三象限,并且在每一個象限內,函數值隨自變量的增大而減小.k<0時,圖象在二、四象限,并且在每一個象限內,函數值隨自變量的增大而增大.如下圖1.
二、轉化物理問題,形成數學的數量關系
1.公式數據化
例如利用速度公式v=s/t得,vt=s.結合數學的反比例函數式,當路程一定,時間和速度成反比例關系.數據如下表1.
進一步尋找時間和速度的變化規律,從下表數據可看出當速度v每增加10 km/h,時間t的減小量不相同,分別為2、1、0.6、0.4cm是逐漸減小的.即當速度的增加量相同時,時間的減小量不斷的變小.數據如下表2:
2.數據圖像化
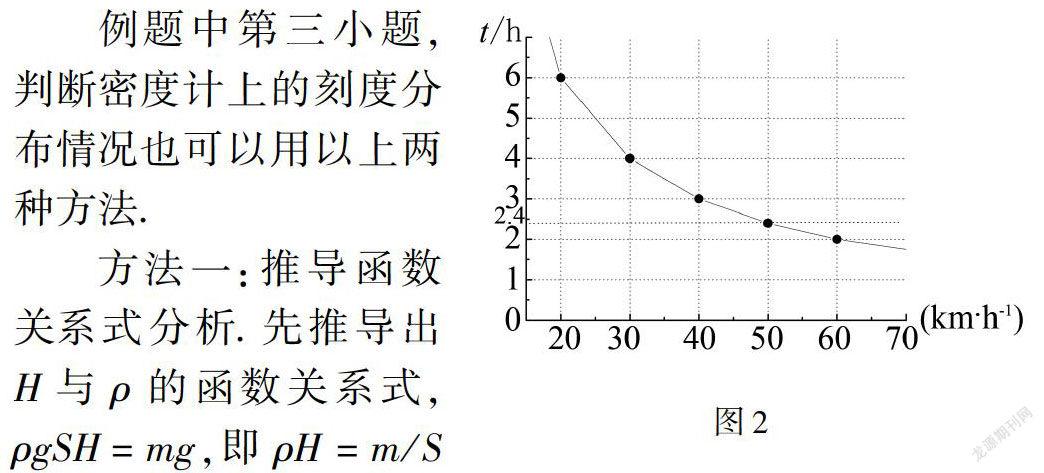
用坐標系x軸和y軸分別表示速度和時間,圖像是一條曲線,如圖2.曲線一端無限靠近y軸,但不與y軸相交;曲線另一端無限靠近x軸,但不與x軸相交,即速度無限小時,時間無限大;速度無限大時,時間無限小.圖中從左往右看,速度的增加量相同時,時間的減小量逐漸減小.
例題中第三小題,判斷密度計上的刻度分布情況也可以用以上兩種方法.
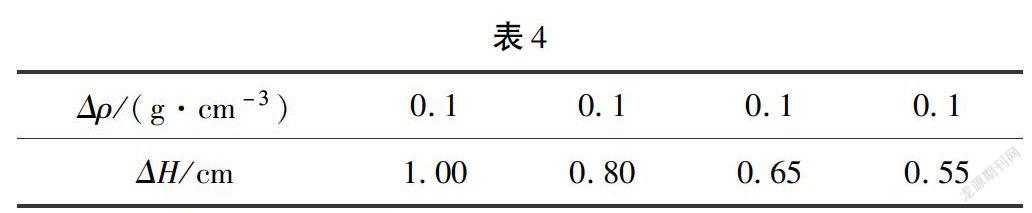
方法一:推導函數關系式分析.先推導出H與ρ的函數關系式,ρgSH=mg,即ρH=m/S(式中ρ表示液體的密度,H表示密度計浸入的深度,m表示密度計的質量,S表示密度計的橫截面積),因m/S是個定值,ρ和H成反比例關系.列舉數據分析.(如表3、表4,表中數據為編造,只用于反映規律)
從數據看,當液體密度ρ每增加0.1 g/cm3
時,密度計浸入的深度H的減小量不相同,分別為1.00、0.80、0.65、0.55cm是逐漸減小的.
方法二:結合圖像分析.如圖3,圖像從左往右看,液體密度的增加量相同時,密度計浸入的深度的減小量逐漸減小.因此越往下,密度計的刻度值越大,且相鄰刻度線的間隔越小.
三、注重分析,滲透數形結合的思想
解答物理題目,借助數形結合的方式,能夠使題目中的物理量關系更加明確和清楚;建立正確的函數關系,簡化題目,加快解題速度.在初中物理教學中,滲透數形結合的思想,使學生的物理思想更豐富,有利于學習能力的提高.
參考文獻:
[1]董倩玉.巧用函數與方程思想解決物理問題[J].數理化解題研究,2018(34):50-51.
[2]康健.物理教學中滲透數學思想方法的探究[J].中學物理教學參考,2017(10):12-13.
[3]楊培軍,王鵬,白文倩.函數和方程思想在物理中的應用[J].物理教學,2016(10):57-59.
[責任編輯:李 璟]

