似是而非卻又神機妙算的估算法

滕澤艷

摘?要：數學是描述數量與空間的學科.高考考試大綱（數學）在考核目標板塊中對能力要求部分明確規定了六個方面的能力為：“空間想象能力、抽象概括能力、推理論證能力、運算求解能力、數據處理能力以及應用意識和創新意識.”而其中的運算求解能力是指“會根據法則、公式進行正確運算、變形和數據處理，能根據問題的條件尋找與設計合理、簡捷的運算途徑，能根據要求對數據進行估計和近似計算.”大多數情況下我們需要進行精確計算，可是，在生活中，特別是在選擇題中，我們會遇到一些不易精確判斷或求解的問題，這時，可以根據具體條件及有關知識，通過大體估計、合理猜想或特殊驗證等手段，準確、迅速地作出大概的估計和近似計算，從而求解.我們把這種方法稱為估算法.

關鍵詞：高考試題;高中數學;解題

中圖分類號：G632文獻標識碼：A文章編號：1008-0333（2020）22-0027-02

歷年高考試題中，有相當一部分選擇題甚至填空題都可以用估算法簡捷地解決.下面通過舉例進行說明，并對其解題一般規律進行歸納與整理.

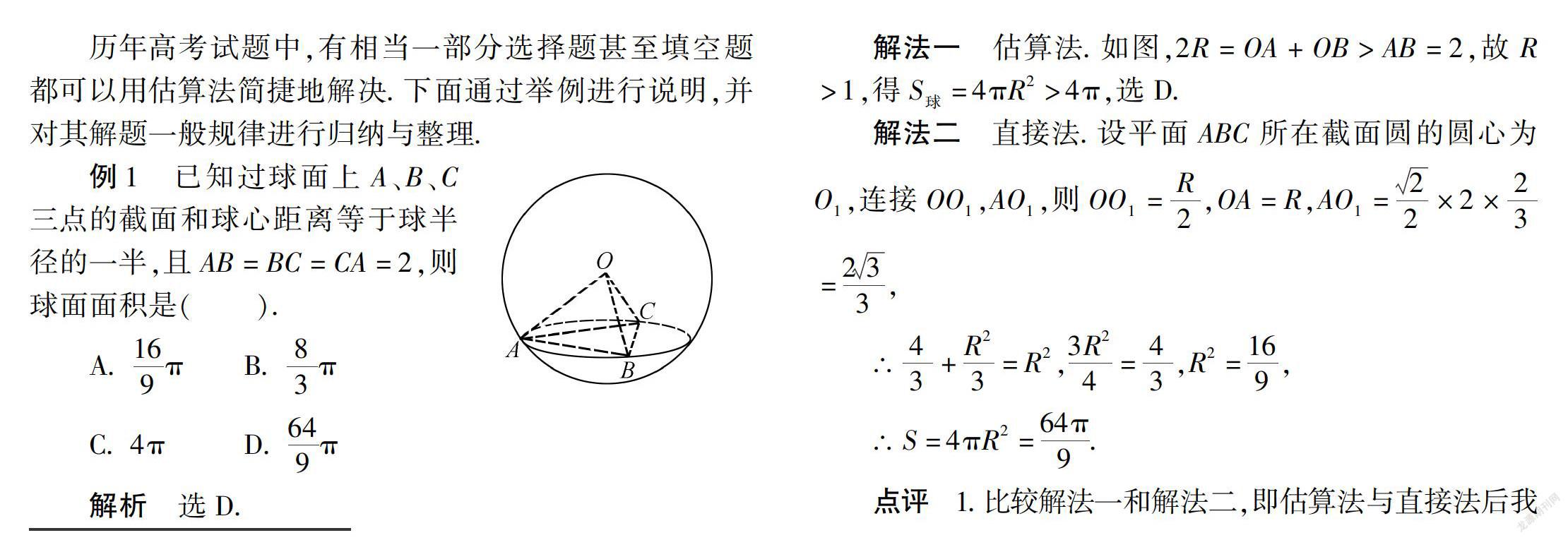
例1?已知過球面上A、B、C三點的截面和球心距離等于球半徑的一半，且AB=BC=CA=2，則球面面積是（）.

A. 169πB. 83π

C. 4πD. 649π

解析?選D.

解法一?估算法.如圖，2R=OA+OB>AB=2，故R>1，得S球=4πR2>4π，選D.

解法二?直接法.設平面ABC所在截面圓的圓心為O1，連接OO1，AO1，則

OO1=R2，OA=R，AO1=22×2×23=233，

∴43+R23=R2，3R24=43，R2=169，

∴S=4πR2=64π9.

點評

1.比較解法一和解法二，即估算法與直接法后我們不難發現，前者僅運用簡單的大小比較（三角形兩邊之和大于第三邊）即選出正確結果，思路清晰，回避了運算.

2.估算法體現了特殊與一般的數學思想方法.

例2?如圖，在多面體ABCDEF中，已知平面ABCD是邊長為3的正方形，EF∥AB，EF=32，EF與平面ABCD的距離為2，則多面體ABCDEF的體積為（）.

A. 92B. 5?C. 6?D. 152

解析?選D.

解法一?估值法.

連接EB、EC.則易得：VABCDEF>VE-ABCD=13×32×2=6.

故排除A、B、C，應選D.

解法二?特殊值法.

所以取特殊情況：即EF⊥面ADE，如圖.取AB與CD的中點M、N，連接MF，NF，作EO⊥AD，垂足為O，則EO⊥平面ABCD.

∴VABCDEF=VADE-MNF+VF-MBCN

=12×3×2×32+13×3×32×2=152.

點評

1.本題中的多面體是非典型的多面體，既非棱柱也非棱錐，直接求體積比較困難.解法一用易求的部分體積“四棱錐E—ABCD”估整體法，極其簡捷.而解法二以特殊圖形求解，由于四個選項均為定值，所以EF的位置并不影響結果，這樣運算也非常簡潔.

2.應用估算法解題的一般步驟為：

（1）根據問題條件，對數學對象（變量或圖形等）進行特殊處理或縮放等;

（2）對處理后的對象進行計算;

（3）根據計算結果估計結論.

例3?函數y=x2+sinx的圖象大致是（）.

解析?選C.

解法一?估算法（取特殊點估算）.

因為函數為奇函數，排除A;當x=10π時，y=5π，排除D;當x=π2時，y=π4+1>0，排除B.選C.

解法二?估算法（以極限位置估算）

當x>0時且無限趨近于0時，y=x2+sinx>0，即圖象在y軸的右邊無限靠近y軸時，圖象應在x軸上方，只能選C.

點評

1.圖形（圖象）類選擇題一般用排除法即可.可以從以下方面進行排除：

（1）特殊點的函數值;

（2）函數的奇偶性、單調性、周期性、對稱性及極限（如漸近線）等.抓住其中其一個某一些性質即可進行排除.

2.估算法一般適用于不易直接求解或不易精確判斷的數學問題.

例4?用1，2，3，4，5這五個數字，組成沒有重復數字的三位數，其中偶數的個數共有（）.

A.24B.30C.40D.60

解析?選A.

解法一?估算法.五個數字中有2個偶數，3個奇數，所以所求偶數個數S小于奇數的個數，即S<12×A35=30，所以選A.

解法二?直接法

先排個位，從2與4這兩個偶數中選一個有2種選法，再從余下的4個數字中任選2個排十位與百位（有序），有4×3=12種，所以，共有選法2×12=24種.選A.

點評

1.解法一巧妙利用奇偶數的對稱性進行估算求解，簡潔明了.

2.常見估算的方法有：

（1）以范圍估定值：即不直接求出定值，而是通過研究所求元素的取值范圍求解;

數形結合列代數式解題，或者反之，借助圖形估算

出數;

（2）以特殊估一般，即選取特例或特殊值對一般性問題進行處理;

（3）取近似值估算.

參考文獻：

[1]么曉江.由n個事件相互獨立所想到的[A].

中國當代教育理論文獻——第四屆中國教育家大會成果匯編（下）[C].2007：11-12P.

[責任編輯：李?璟]