數形結合思想在小學數學中的應用

陳彪

摘要：數學教學就是為了更好的培養學生的邏輯思維和數學精神，那么在新課程改革不斷推進的今天，教師教學還需要關注學生思維品質的提升。數形結合的教學方法在數學教學中得到了非常廣泛的運用，那么如何進行具體的使用還需要本文做出分析和研究。基于此本文結合實例對數形結合思想在小學數學教學中的應用做出闡述。

關鍵詞：數形結合思想;小學數學;應用

“數”及“形”是數學內兩個最基本概念，數能讓形量化，形可使數更為形象。數學教學中數形結合，將數學中數量關系、運算等同圖形結合思考，可讓數形間優勢互補。小學為數學啟蒙階段，將數形結合思想應用到小學數學教學中，能幫助學生順利構建數學模型，學好數學，提高教學成績。

一、用直尺感知數形結合

小學生對數列規律難以理解，教學中可以借助學生熟悉的直尺對數列進行講解。教學中可將直尺當作是“數尺”，也就是可以將抽象的數在熟悉的可以看見的數尺（只有自然數，不存在刻度）上進行有方向、有規律的排列，將抽象數在數尺上直觀形象展示，這樣不僅可以幫助學生理解數的大小、順序，還能幫助他們對數列規律簡單理解。

二、用線段圖理解數量關系

小學生對數量關系難以理解，遇到題目不知道如何入手，而線段圖則可以讓抽象的數量關系變得形象，易于理解。在遇到“求比一個數的幾倍還多幾（少幾）”這類應用題時，單純列式計算，學生很容易出現理解錯誤，但是結合線段圖之后，理解就容易多了。

例如，學校給校內班級配備籃球、排球兩種體育用品，其中排球個數為6個，籃球個數為排球數量的4倍少兩個，求學校配備的籃球有多少個？

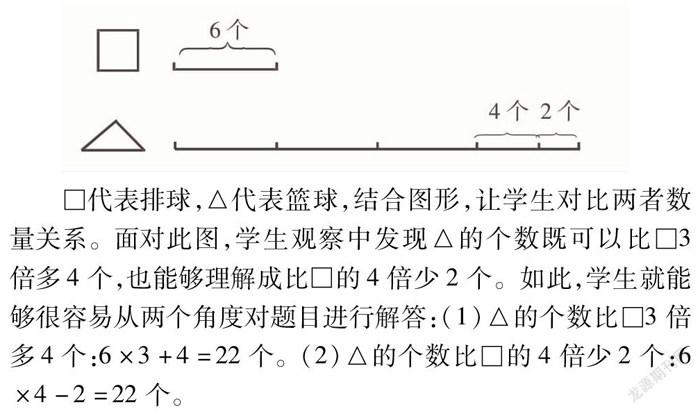
學生對于“幾倍少幾”“幾倍多幾”這類的題目難以理解，為使學生理解更為容易，教學中可設計如下圖形：

□代表排球，△代表籃球，結合圖形，讓學生對比兩者數量關系。面對此圖，學生觀察中發現△的個數既可以比□3倍多4個，也能夠理解成比□的4倍少2個。如此，學生就能夠很容易從兩個角度對題目進行解答：（1）△的個數比□3倍多4個：6×3+4=22個。（2）△的個數比□的4倍少2個：6×4-2=22個。

通過上面的例子可以看出解題中，線段圖能夠讓“看不見”變得“清晰可見”，通過線段圖，學生可以清晰看出兩個物體間的數量關系，拓寬解題思路，從而可以將復雜的解題過程變得更為簡單，輕松解決問題。

三、用圖形解決容斥、行程問題

小學數學教學中，容斥問題、行程問題也是學生容易出錯的兩類題目，而如果教學中進行數形結合，通過圖形去解決問題，問題就會迎刃而解了。

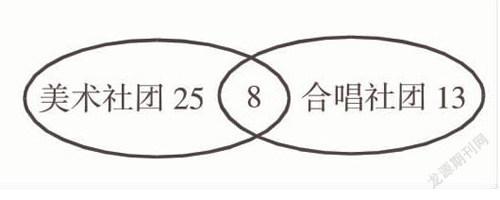
如，五年級三班所有同學都至少參加了一項興趣社團，其中參加美術社團的有33人，參加合唱社團的有21人，并且有8人兩個社團都參加了，問班上的學生人數總共是多少？

解題中可以先畫一個如上圖所示的圖形，從圖中能對學生社團參加情況一目了然，能清晰看出8人是重復的那部分，也就可以順利得出班上學生總人數：33+21-8=47（人）。

行程問題，特別是變速行程問題是小學階段學生難以理解的一類題目，在沒有學習過“二元一次方程”情況下，學生對行程問題中的數量關系用圖形進行表示的話就會讓題目變得很容易。

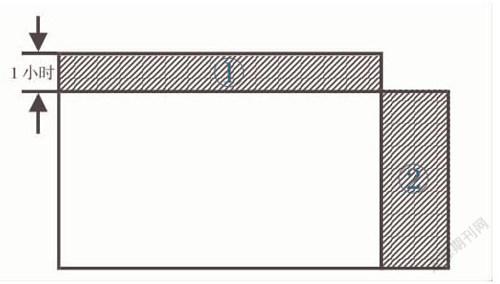
如，小張開車從甲地去乙地送貨，如果他將車速提高20%的話，可以提前1小時到達;但若是按照原速行駛120km之后，將車速提高25%的話，則可提前40分鐘到達目的地。求兩地的距離？

此題可以用長方形面積方法來解決，按照第一種走法，可畫出上圖，面積代表總路程，長為速度，寬為時間，不論長寬怎樣變化，總路程不變，長方形面積相等，則按照這樣理解，上圖中長方形①的面積等于長方形②的面積，就可以列出：原速度×20%×（原時間-1）=原速度×1，從而求出原時間=6小時。

綜上所述，小學數學教學中，應用數形結合思想，能將抽象數學問題進行直觀展示，使學生的解題思路更加形象化，進而激發學生的學習興趣，順利解決數學問題，使數學教學趣味性更強，讓教學達到事半功倍的效果。

參考文獻

[1]范小發.數形結合思想在小學數學教學中的應用[J].當代教研論叢，2016（11）：50.

[2]趙麗娜，李鵬.淺析數形結合思想在小學數學教學中的滲透教學[J].課程教育研究，2016（28）：130-131.