試題解析
何婷

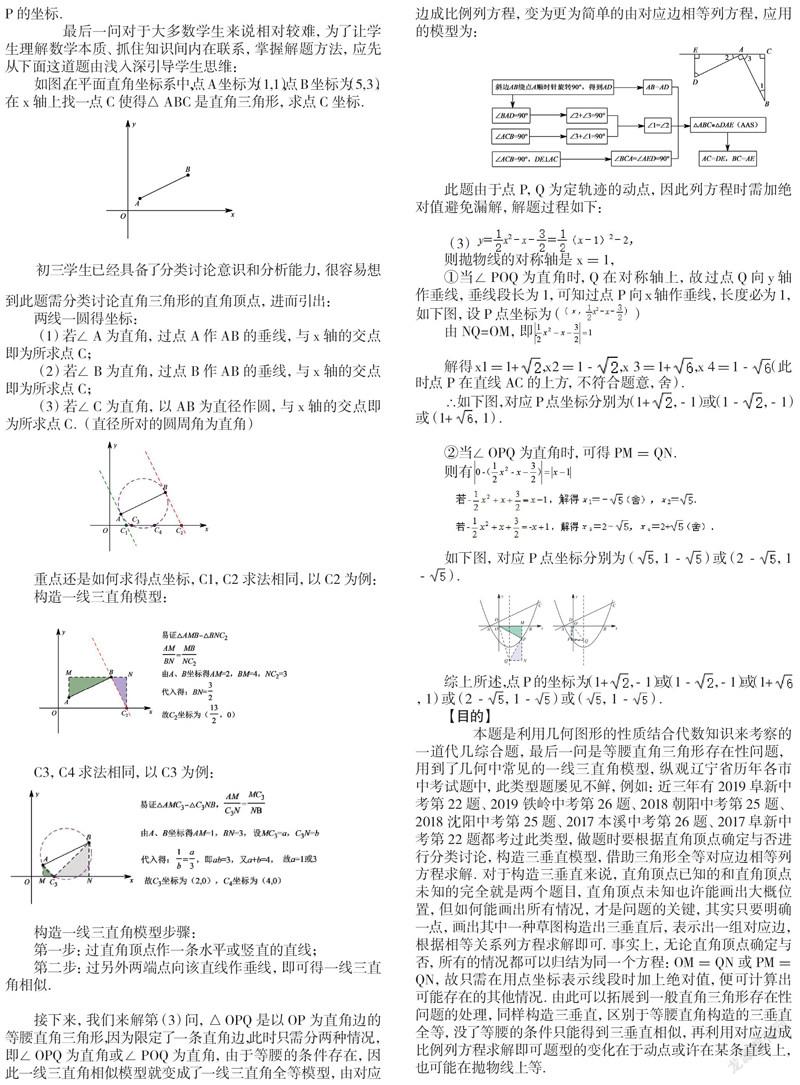
【問題】
(2017本溪)如圖,在平面直角坐標系中,拋物線y=與x軸交于A,B兩點,點B(3,0),經過點A的直線AC與拋物線的另一交點為C(4,),與y軸交點為D,點P是直線AC下方的拋物線上的一個動點(不與點A,C重合).
(1)求該拋物線的解析式;
(2)過點P作PE⊥AC,垂足為點E,作PF∥y軸交直線AC于點F,設點P的橫坐標為t,線段EF的長度為m,求m與t的函數關系式;
(3)點Q在拋物線的對稱軸上運動,當△OPQ是以OP為直角邊的等腰直角三角形時,請直接寫出符合條件的點P的坐標.
【背景】
1.試題出處:本題選自2017年本溪市中考數學試題的26題,是一題三問的二次函數代幾綜合題,第一問為待定系數法求二次函數表達式,第二問為運用相似求兩個參數之間的關系,第三問為直角三角形存在性問題,此題適合于初三學生在中考綜合復習時使用.
2.涉及知識點:待定系數法求一次函數、二次函數表達式;三角形相似;等腰直角三角形性質、三角形全等、垂直定義.
3.涉及思想方法:函數與方程、轉化與化歸、分類討論、模型思想、類比思想.
4.題目難點:
(1)學生代數幾何綜合解題能力較弱,難以尋找解題思路;
(2)學生將復雜問題轉化為已學習的基本模型問題的能力較弱.
【任務】
學生經過了初中三年的學習,已經掌握了三角形全等、三角形相似及二次函數的相關知識,能夠熟練運用全等的性質和判定解決問題,能夠運用三角形相似求線段長、確定兩個參數之間的關系,也具備了一定的推理及運算能力,但學生將代數、幾何知識綜合運用的能力較弱,故講解時應注重解題策略分析、方法歸納,引導學生逐步具備將復雜問題轉化為已學習的基本模型問題的意識尤為重要。
【分析】
第一問待定系數法確定二次函數表達式學生掌握較好,這里就不再講解,提醒學生計算一定要準確,表達式是解答后面兩問的前提。
審題及解題策略分析
問題(2)過點P作PE⊥AC,垂足為點E,作PF∥y軸交直線AC于點F,設點P的橫坐標為t,線段EF的長度為m,求m與t的函數關系式.
抓住已知和隱含條件分析解題思路:
解題過程如下:
問題(3)點Q在拋物線的對稱軸上運動,當△OPQ是以OP為直角邊的等腰直角三角形時,請直接寫出符合條件的點P的坐標.
最后一問對于大多數學生來說相對較難,為了讓學生理解數學本質、抓住知識間內在聯系,掌握解題方法,應先從下面這道題由淺入深引導學生思維:
如圖,在平面直角坐標系中,點A坐標為(1,1),點B坐標為(5,3),在x軸上找一點C使得△ABC是直角三角形,求點C坐標.
初三學生已經具備了分類討論意識和分析能力,很容易想到此題需分類討論直角三角形的直角頂點,進而引出:
兩線一圓得坐標:
(1)若∠A為直角,過點A作AB的垂線,與x軸的交點即為所求點C;
(2)若∠B為直角,過點B作AB的垂線,與x軸的交點即為所求點C;
(3)若∠C為直角,以AB為直徑作圓,與x軸的交點即為所求點C.(直徑所對的圓周角為直角)
重點還是如何求得點坐標,C1,C2求法相同,以C2為例:
構造一線三直角模型:
C3,C4求法相同,以C3為例:
構造一線三直角模型步驟:
第一步:過直角頂點作一條水平或豎直的直線;
第二步:過另外兩端點向該直線作垂線,即可得一線三直角相似.
接下來,我們來解第(3)問,△OPQ是以OP為直角邊的等腰直角三角形,因為限定了一條直角邊,此時只需分兩種情況,即∠OPQ為直角或∠POQ為直角,由于等腰的條件存在,因此一線三直角相似模型就變成了一線三直角全等模型,由對應邊成比例列方程,變為更為簡單的由對應邊相等列方程,應用的模型為:
【目的】
本題是利用幾何圖形的性質結合代數知識來考察的一道代幾綜合題,最后一問是等腰直角三角形存在性問題,用到了幾何中常見的一線三直角模型,縱觀遼寧省歷年各市中考試題中,此類型題屢見不鮮,例如:近三年有2019阜新中考第22題、2019鐵嶺中考第26題、2018朝陽中考第25題、2018沈陽中考第25題、2017本溪中考第26題、2017阜新中考第22題都考過此類型,做題時要根據直角頂點確定與否進行分類討論,構造三垂直模型,借助三角形全等對應邊相等列方程求解.對于構造三垂直來說,直角頂點已知的和直角頂點未知的完全就是兩個題目,直角頂點未知也許能畫出大概位置,但如何能畫出所有情況,才是問題的關鍵,其實只要明確一點,畫出其中一種草圖構造出三垂直后,表示出一組對應邊,根據相等關系列方程求解即可.事實上,無論直角頂點確定與否,所有的情況都可以歸結為同一個方程:OM=QN或PM=QN,故只需在用點坐標表示線段時加上絕對值,便可計算出可能存在的其他情況.由此可以拓展到一般直角三角形存在性問題的處理,同樣構造三垂直,區別于等腰直角構造的三垂直全等,沒了等腰的條件只能得到三垂直相似,再利用對應邊成比例列方程求解即可.題型的變化在于動點或許在某條直線上,也可能在拋物線上等.

