“開放”情境：促進學生深度理解

張鴻森

【案例背景】——經典問題，典型錯誤

抽屜原理是人教版數學六年級上冊數學廣角內容，《抽屜原理》是大家公認的經典課題。然而，在實際教學中，一線教師往往會引導學生從“平均分”角度理解，通過除法計算解決問題，結果使得學生在解決這類經典問題時錯誤率高，而且重復錯誤。比如：10個蘋果放在9個抽屜里，總有一個抽屜至少放（? ）個蘋果。學生學會的方法是“10÷9=1（個）……1（個）”，學生更容易理解接受的答案是“總有一個抽屜至少有1個蘋果”，也就是把10個蘋果平均分成9份，每份至少1個蘋果，至多有“1+1=2個蘋果”，這才是學生最真的思考結果。其實借助“開放”情境可以引導學生經歷自主探索、比較分析、建立抽屜原理直觀表象，有助于學生深度理解“總有”和“至少”的含義。

基于以上分析，筆者模仿朱國榮特級教師的思路設計了《抽屜原理》一課，主要通過“開放”情境，讓學生經歷梳理問題情境、比較分析、發現共性的過程，直觀深入理解抽屜原理。

【原始情境再現與剖析】——“不理解”只能“記模型”

1 分鉛筆：學生無法理解“至少”的含義

抽屜原理問題中的“至少”往往給孩子一種指向“少”的暗示，要想每個抽屜少放一點，學生通常會想到“平均分”的方法，自然會和除法建立聯系，通過除法計算解決問題。

【片段回放】

出示例題：把4支鉛筆放入3個抽屜中，總有一個抽屜至少放幾支鉛筆？

要求：獨立解決問題，并和同桌交流你的想法。

預設1：列除法算式解答。預設2：逐一列舉放的方法。

反饋1：4÷3=1（支）……1（支），1+1=2（支）。學生在講解算式及思路時，普遍認為要每個抽屜放的少就要盡可能“平均分”，所以用除法計算。也有同學說興趣班老師就是這樣教的。

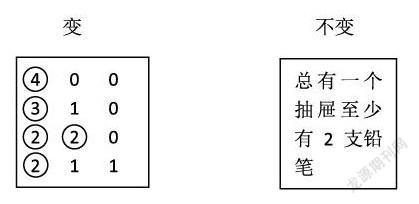
反饋2：4、0、0;3、1、0;2、2、0;2、1、1。學生的結果是有一個抽屜至少1支或0支。

在反饋的過程中沒有學生畫圖解決問題，筆者只能順應學生計算的方法生硬地講解“總有”和“至少”的含義，整個過程學生都是被動地聽，通過聽講解記住“除法計算”的模型，完全不能理解“至少”的含義。

2 問題剖析：“封閉”情境讓學生思維停留在模仿和記憶層面

（1）“封閉”情境問題不能激發學生興趣和挑戰欲望，學生只需要用已有模型解決問題即可，不需要理解“總有”和“至少”的含義。

（2）學生用列舉方法解決問題，教師沒有幫助學生比較辨析，容易干擾學生除法計算結果，讓學生的思維更模糊。

（3）教師順應學生計算解題的方法生硬的講解，是在用抽象的語言講述抽象的問題，學生缺少自主探索、自主感悟，后續練習仍然只能是模仿。

【調整后情境及價值分析】——“激活思維”與“深度理解”

3 自主選擇：激發學生興趣，激活學生思維

到底什么情境能激發學生興趣，激活學生思維，有利于學生自主建構、直觀理解“總有”和“至少”的含義。筆者設計了兩種分鉛筆的方案讓學生選擇的情境。自主選擇是學生的興趣點，未提供結果的方案具有挑戰性，需要學生自主探索、比較分析去尋找答案，筆者認為這就是“開放”情境。

【片段回放】

呈現情境：有4支鉛筆。（1）小明直接拿了2支，開心走了。（2）老師把4支鉛筆放入3個抽屜（抽屜是敞開的），等老師放好后小明選擇一個抽屜里的拿走。

師：如果你是小明，你會選擇方案（1）還是方案（2）？為什么？

A.無所謂? ? B.選方案（1）? ? C. 選方案（2）? ? ?D. 有所謂

討論中，學生建議先梳理方案（2）有幾種放法。（4、0、0;3、1、0;2、2、0;2、1、1）

師：用一句話告訴小明，為什么選擇方案（2）不選擇方案（1）？

生：選擇方案（1）只能拿2支鉛筆，選方案（2）至少拿2支鉛筆。

師：方案（2）至少能拿到2支鉛筆，是這樣嗎？我們一起來看看：

生：第一種方法可拿走4支鉛筆，第二種方法可拿走3支鉛筆，第三種、第四種方法可拿走2支鉛筆。

師：不同的放法，什么在變？什么沒變？

生1：不同的放法，每個抽屜里鉛筆的數量在變化。

根據學生匯報小結：總有一個抽屜至少有2支鉛筆。

師：這里的“至少”是什么意思？

生1：放得最多的一個抽屜至少放2支鉛筆。

生2：我們可以畫圖理解：放得最多的一個抽屜至少放2支鉛筆。

4 “開放”情境：促進學生深度理解

課程標準指出：教師的教學要以學生的已有知識和經驗為基礎;教師的教學要有利于激發學生的學習興趣，有利于激活學生思維，引發學生數學思考。自主選擇分鉛筆方案是學生熟悉的情境，同時具有挑戰性，需要學生靜心思考，這些讓學生深度理解抽屜原理變得自然且可能。

4.1 自主選擇，激發學習興趣

在片段中，教師提供的兩種方案，讓學生扮演小明自主選擇，學生的學習興趣馬上起來了，積極舉手，都想表達自己的選擇想法。在這個環節中，教師沒有及時評價，也沒有肯定或否定學生的選擇，讓學生始終保持積極的好奇心，這就為學生后續的深入思考提供了保障。

4.2 完善方案，引發深度思考

學生充分經歷探究過程才會有深刻體驗。在新情境中，教師用“用一句話告訴小明，為什么選擇方案（2）不選擇方案（1）？”激活學生思維，引發學生思考，學生把目光聚焦到兩種方案的比較上。要想得出選擇方案的結果，學生必然要對方案（2）的四種具體放法進行深度思考，找尋出方案（2）相比方案（1）的優越性。學生經歷比較過程發現方案（2）的四種放法中每個抽屜鉛筆支數在變化，但總有一個抽屜里鉛筆數多一些。同時，畫圖的方法可以直觀比較四種放法最多的一個抽屜中鉛筆支數，深刻感悟到“至少”是指最多的一個抽屜中“至少”有幾支鉛筆。學生經歷列舉比較和畫圖比較兩層深度思考，直觀、自然地理解了“總有”和“至少”的含義，筆者認為這就是深度學習。

（作者單位：浙江省杭州市申花小學）