問題導向結合數學建模在“數學物理方法”教學中的應用

王秋玲，張開銀，劉乙飛，范 沁，崔北臣

（1.武夷學院機電工程學院，福建武夷山354300；2.阜陽師范大學物理與電子工程學院,安徽阜陽236037）

0 引言

數學物理方法是高等學校理工科專業的一門重要基礎課，定位在高等數學和普通物理的基礎上，以講授求解數學物理問題的常用古典方法為主，同時注重介紹實際物理問題的數學建模應用。該課程與電動力學、量子力學、流體力學、熱學、聲學、工程等問題和理論有密切聯系，目的是培養學生用數學語言表述物理問題、綜合應用數學工具解決物理問題的能力，為學習后續專業課程和擴大數學知識面提供必要的數學基礎[1]。它是以研究物理問題為目標的數學理論和數學方法，主要包含復變函數、積分變換和偏微分方程等內容。其中，復變函數和積分變換主要是數學內容，知識點邏輯性強，涉及的物理學知識比較少，學生接受相對容易一些。而偏微分方程多起源于連續介質力學、傳熱學和電磁場理論，在介紹這些方程的時候，經典教材使用的物理學問題相對單一，呈現的物理學問題大都是理想化的，而且大都偏重于數學理論，強調偏微分方程的解析求解方法[2]。

教材中此類偏微分方程的定解問題包括泛定方程、初始條件和邊界條件，求解方法隨泛定方程和定解條件的變化差異極大[3-4]。以輸運問題為例，教學過程中，往往從最基本的無限長均勻桿熱傳導方程開始，推演到二維、三維熱傳導方程，求解方法隨逐步增加的限制條件完全不同。從行波法求解半無限長均勻桿溫度分布問題開始，增加限制到第一、二和三類邊界條件則需要用分離變量法求解，最后至非齊次方程的定解問題時需要用沖量定理法處理。盡管教材中的例題通常具有明確的物理意義，但是要從內容繁多，公式推導繁雜的數學推理及其數學表達式中看出所要表達的物理圖像，不僅對學生的數學基礎要求較高，還需要一定的專業知識基礎。自1999年高等教育大規模擴招以來，高等教育已經完全轉變為大眾教育，多數高校擴招后學生的數學與物理功底已大不如從前。在重視數學理論的基礎上，如何增強學生的學習興趣，因材施教，提高教學和學習效果，是一個值得廣泛而且深入研究的問題。

1 問題導向學習與數學建模培訓相結合的策略

最近幾年，慕課和翻轉課堂等啟發式教學得到了廣泛認可，是當前教學改革的潮流，能夠有效開發學生的自主學習潛能。而問題導向學習（Problem based learning，PBL）更是強調學生的中心地位，鼓勵學生組成科研、學習小組，激勵學生以團隊形式就各種有意義的個案，比如科研難題、工程案例等，進行問題分析、解決和經驗總結等。吳建成等人針對需要本碩銜接的課程教學，提出了PBL的十個問題表單并列舉了解決具體問題的七個步驟[5-6]。問題導向學習可以高效激發自主學習能力、問題解決能力和協作交流能力。在問題導向學習中，學生是主體，問題是導向。該模式在一門課程中的應用能否成功，科學、生動、有趣的問題設計是關鍵，需要教師和教輔人員投入相當的精力和時間，考驗非常大。

在大多數高校的人才培養方案中，數學物理方法一般安排在大二下學期開設。在這個階段，學生已經學習了“高等數學”、“線性代數”、“大學物理”、“C程序設計”、“Matlab”、“計算物理”等相關知識，具備了數學建模和數值計算的基本能力，經過一定的培訓可以參加全國大學生數學建模競賽。在數學建模培訓過程中，學生會接觸到多種類型的物理、工程、統計等實際問題。特別是指導老師，經過多年的積累往往收集了大量的類型多樣的案例，其中會有相當數量的案例與數學物理方法課程的相關知識點特別是偏微分方程相關。如果將這些案例進行分類整理，并補充一些來自生活實踐的案例，豐富問題導向學習的案例庫，既能增加課程的趣味性，提高學生的學習興趣，也能消除學生的畏懼和消極心態，激發好勝心，使數學物理方法課程成為一門學生愿意學習并能為其所用的課程，達到事半功倍的學習效果。

以高教社杯全國大學生數學建模比賽題目為例，我們對2010年到2019年的題目進行了分析，發現能夠與物理學和數學物理方法或多或少有一定的聯系的題目有近10道。以這些題目為背景，教師可以根據教學需要進行一定的改造，從而變化出一定數量的個案，豐富問題導向學習的案例庫供教學學習使用。當然，其中的個別案例與課程關聯度不是很強，需要教師結合物理、工程等實際問題進一步提煉出更多更有趣更有意義的案例，比如結合學生的專業特點選取一些生產實踐的實際問題作為應用案例。把這些實例與教學內容結合起來應用到課堂教學中去，使學生了解數學知識是怎樣應用于實際，怎樣解決實際問題，有利于打破書本與實際的界限，實現數學與應用物理學科之間相互滲透、交叉，緊密結合實際生產中的問題，綜合運用數學理論分析和解決實際問題，形成“學”與“用”的良性循環。

在建立了融合數學建模訓練的問題導向學習案例庫的基礎上，鼓勵學生大膽學習并應用計算軟件，例如C程序、Matlab、Orign和Excell等，將傳統教學手段與計算機仿真相結合，改變只用符號和復雜數學公式教學的模式，使得學生對復雜、抽象和煩瑣的數學物理問題具有更深刻的理解。

2 教學案例

以2018年的一道數學建模題“高溫作業專用服裝的設計”為例，探究在教學過程中以問題導向結合數學建模思維，培養學生應用數學方法解決實際問題的能力。在此，我們先對該案例做個簡單重述。在高溫環境下工作時，人們需要穿著專用服裝以避免灼傷。專用服裝通常由三層織物材料構成，記為I、II、III層，其中I層與外界環境接觸，III層與皮膚之間還存在空隙，將此空隙記為IV層。為設計專用服裝，將體內溫度控制在37°C的假人放置在實驗室的高溫環境中，測量假人皮膚外側的溫度。為了降低研發成本、縮短研發周期，需要利用數學模型來確定假人皮膚外側的溫度變化情況。如給定專用服裝材料的某些參數值由表1給出，對環境溫度為75°C、II層厚度為6 mm、IV層厚度為5 mm、工作時間為90分鐘的情形開展實驗，測量得到假人皮膚外側的溫度。建立數學模型，計算溫度分布。

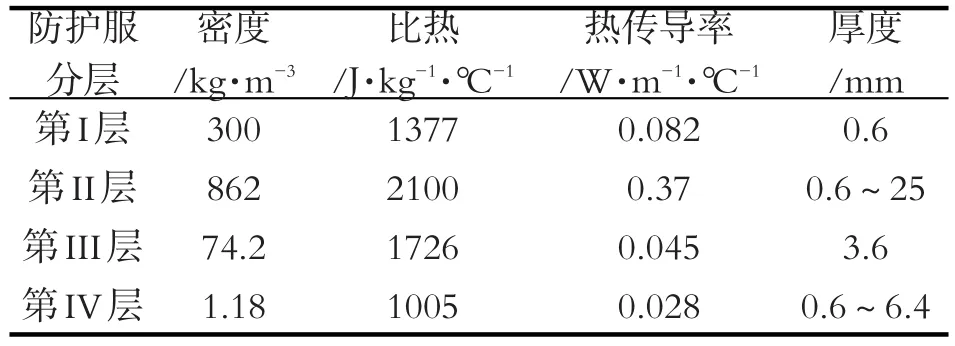
表1 防護服的物理屬性

首先引導學生將負責的問題理想化，并將此問題近似為一維輸運問題，也就是如圖1所示的環境-熱防護服-假人構成的系統。本問題考慮的環境溫度較低，熱輻射效應遠小于熱傳遞，因此其影響可以忽略不計。防護服各層之間、防護服內層與空氣之間、空氣層與假人皮膚之間的溫度分布都是連續的，通過界面的熱流通量連續[7]。

圖1：空氣層-高溫作業專用服-假人皮膚層系統

該系統可用的輸運方程（1）表示，而且系統密度、比熱容以及熱傳導系數等均為位置依賴的參數。

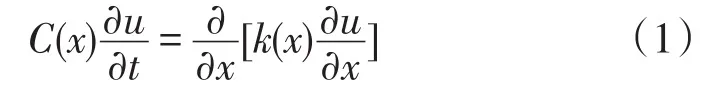
系統顯熱容函數為

其中ρi、ci、di分別表示系統第i層材料的密度、比熱容和厚度。系統熱傳導函數為

其中ki表示系統第i層材料的熱傳導系數。

系統的初始條件為

系統的邊界為外殼層左邊界面和假人皮膚層右邊界面。假定系統兩端界面均按照牛頓冷卻定律散熱[5]，即

其中Hshell和Hskin分別為殼層和假人皮膚層的熱對流系數，uL和uR分別為外界環境溫度和假人內部溫度。

方程（1）～（6）構成了描述熱防護服熱量輸運過程的定解問題，求解該定解問題可獲得系統溫度隨空間和時間的分布。在Matlab軟件工具箱中有個pdepe函數，可以用來求解上述偏微分方程。該函數求解形式形如式（7）的偏微分方程。

該式中第一項指顯熱容隨空間時間的變化梯度；第二項指的是熱量隨空間時間的變化梯度；第三項指的是熱源隨空間時間的變化梯度。pdepe函數的調用格式為：sol=pdepe(m,@pdefun,@pdeic,@pdebc,x,t)，其中輸入函數@pdefun指的是PDE的問題描述函數，@pdebc指的是PDE的邊界條件描述函數，@pdeic指的是PDE的初始條件，輸出函數sol指的是一個三維數組，sol(:,:，1)表示一維系統溫度函數u的解。

在初始條件方程（4）中有u0=37°C，同時邊界條件方程（5-6）中uL=75°C，uR=37°C。由于殼層材料和假人材料未知，在求解問題時參數Hshell和Hskin作為可調參數，并引導學生進行對比分析。調節參數Hshell和Hskin，獲得問題的解，輸出假人皮膚處溫度隨時間的變化關系，與實驗測定的假人皮膚溫度變化實驗數據進行比較，確定最優參數值。圖2是參數Hshell和Hskin取不同參數值時模擬得到的假人皮膚溫度隨時間的變化關系曲線。由圖2可知，參數Hshell對曲線前期時間段的溫度分布影響明顯，而參數Hshell則對系統達到穩恒狀態的后期溫度分布影響明顯。Hshell和Hskin取值為10和4.4時得到的模擬曲線與實驗數據符合的非常好。

圖2 假人皮膚溫度隨時間的分布

高溫防護服的熱傳導過程是典型的輸運方程定解問題。通過該案例的訓練，不僅可以使學生學到有關的基礎知識，而且可以引導學生通過對具體物理過程的具體分析，抓住主要因素、進行必要的簡化近似、建立數學模型來求解和對比分析，從而對該過程有較深的理解。

3 教學效果評價

結合數學建模培訓的問題導向學習在數學物理方法的教學中的作用，主要用于解決學生以下幾個問題：學習被動、學時不足、學科交叉不突出和科學應用的思維欠缺。就像上文所述的，問題導向中的案例庫是一個關鍵。構建有趣有意的案例庫，能夠觸發學生的好奇心，吸引學生主動參與，課后多思考多練習，自然也就增加了課時。科學的教學效果評價，能夠有助于教師和教學輔助人員更好地改進案例庫，更好地調動學生的學習熱情。

為此，可以從以下三個方面對基于數學建模培訓的問題導向學習方法進行評價：①考查學生對知識點的掌握。這是一個短期效果的評價，一般在學期末課程結束的時候，通過考查考試等形式，檢查學生對數學物理方法的整體認識和各個知識點的系統性理解和把握；②考查學生對數學物理方法相關知識的應用。這個可作為中期效果評價，一般在學習量子力學、材料力學等專業課的時候，調研學生對數學物理方法各個知識點在相關課程中的靈活應用情況，從而進一步反饋教學效果，反映學生對學科交叉知識的靈活運用；③考察學生的科學素養。這個一般在大學生畢業前做調研，重點從競賽、畢業論文設計和職業發展等多個角度進行評價反饋。比如全國大學生數學建模競賽可以直觀地反饋問題導向學習結合數學建模培訓的方法在數學物理方法教學中的作用。畢業論文設計更能夠客觀地反映數學物理方法在畢業設計中的應用程度，反映學生對該課程的掌握及其靈活應用解決問題的能力。

我們的調研發現，與傳統教師主導、學生被動參與的教學模式相比，基于問題導向學習并結合數學建模培訓思想和案例庫的方法能使學生深刻地感受數學物理方法知識在實際學習和生活中的應用，增強學習興趣。同時開展一定的數值模擬計算，將結果可視化，更直觀地呈現出來，提高了教學效果，不僅使學生的數學物理方法學的比較扎實，而且在數學建模競賽中也取得了良好成績，一舉多得，事半功倍。

4 結束語

本文以三大類方程中的輸運方程教學為例，介紹了在教學中根據學生的專業特點把生活中的一些實際問題與知識點聯系起來，教學中融入數學建模思維，將抽象的數學內容具體化，積極引導學生進行問題導向學習。這樣可以使學生切實體會數學物理方法的應用價值，增強數學物理方法的學習興趣和主動性，并提高學生應用數學知識分析和解決實際問題的能力。通過實踐教學提高學生的學習興趣，可以顯著提升教學效果，達到事半功倍的良好效果。