關于矩陣乘積秩的一種簡捷證明
2020-09-11 13:41:32孔妮娜北方民族大學數學與信息科學學院寧夏銀川750021
數學學習與研究 2020年11期
◎孔妮娜 (北方民族大學數學與信息科學學院,寧夏 銀川 750021)
一、基本概念及定理
已知矩陣
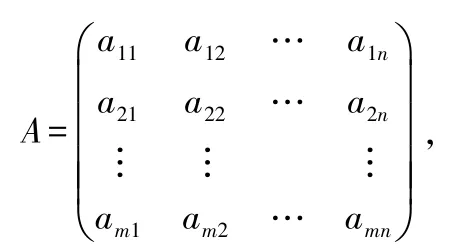
如果把矩陣A的每一行看成一個向量,則

稱為矩陣A的行向量組.
如果把矩陣A的每一列看成一個向量,則
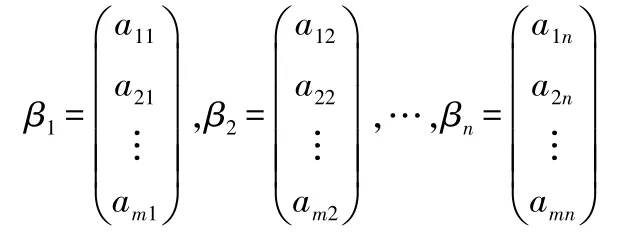
稱為矩陣A的列向量組.
定義[1]矩陣A的行向量組的秩稱為矩陣A的行秩,矩陣A的列向量組的秩稱為矩陣A的列秩,且矩陣A的行秩與列秩相等,統稱為矩陣A的秩.
參考文獻[1]中給出的關于矩陣乘積秩的定理如下:
定理[1]設A是數域P上s×n矩陣,B是數域P上n×m矩陣,于是

即矩陣乘積的秩不超過各因子的秩.
二、主要結果
本文用一種簡捷的方法證明了矩陣乘積秩定理,并舉例說明定理的結論成立.
定理的證明要證明式(1)成立,只需要證明秩(AB)≤秩(A),同時秩(AB)≤秩(B).下面分別證明這兩個不等式.
(1)首先證明秩(AB)≤秩(B).
已知
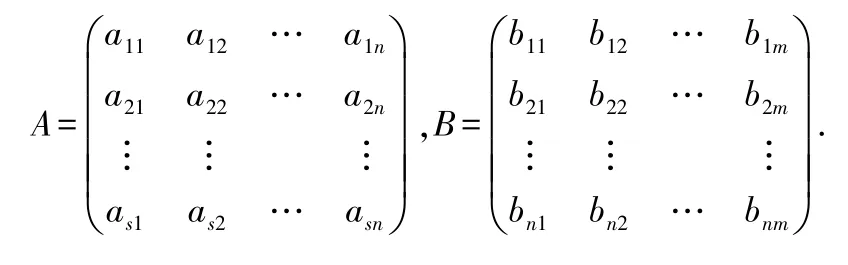
設β1,β2,…,βn表示矩陣B的行向量組,則
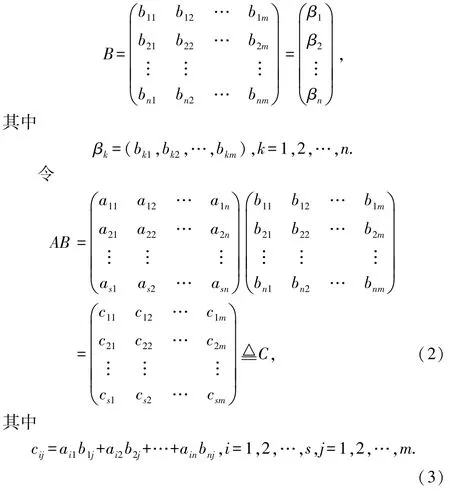
則矩陣C的第i行元素分別為
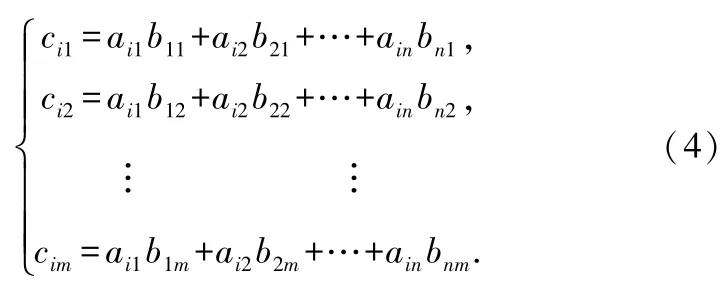
令γ1,γ2,…,γs表示矩陣C的行向量組,則

把式(4)帶入式(5),得
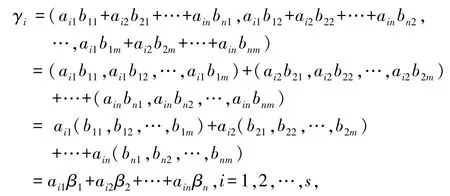
即矩陣C的行向量組γ1,γ2,…,γs可以由矩陣B的行向量組β1,β2,…,βn線性表出,所以


(2)其次證明秩(AB)≤秩(A).
令α1,α2,…,αn表示矩陣A的列向量組,則
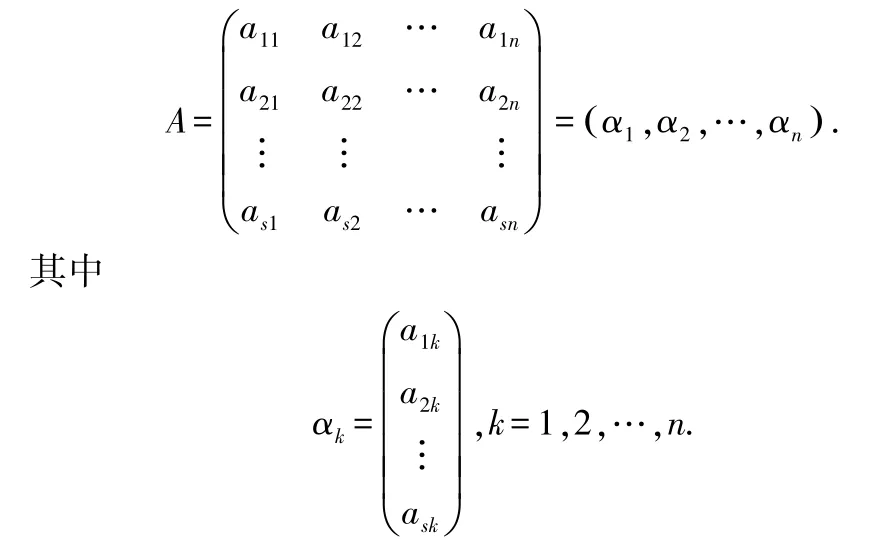
由式(2)和式(3)可知,矩陣C的第j列元素分別為
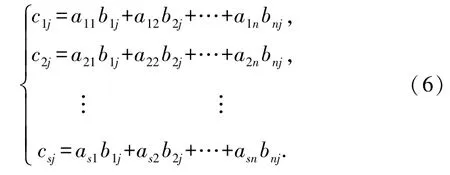
如果令μ1,μ2,…,μm表示矩陣C的列向量組,則
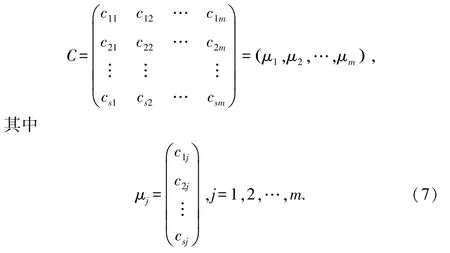
把式(6)帶入式(7),得

即矩陣C的列向量組μ1,μ2,…,μm可以由矩陣A的列向量組α1,α2,…,αn線性表出,所以
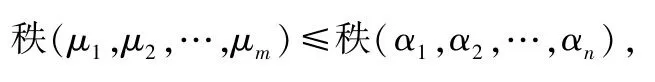

綜上所述,結論成立.
例已知矩陣
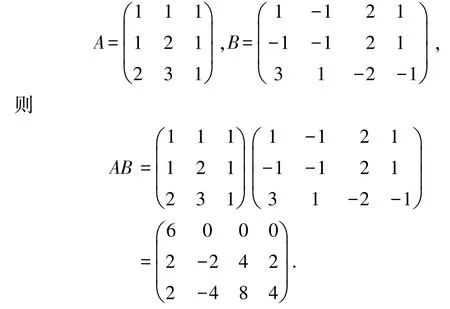
下面利用矩陣的初等行變換分別計算矩陣A、B及AB的秩:


