求收斂的數項級數“和”的若干典型方法
◎黃毅蓉 (成都航空職業技術學院,四川 成都 610100)
1 引言
2 方法論述
2.1 利用數項級數自身求數項級數的“和”
2.1.1 直接求解法(定義法)
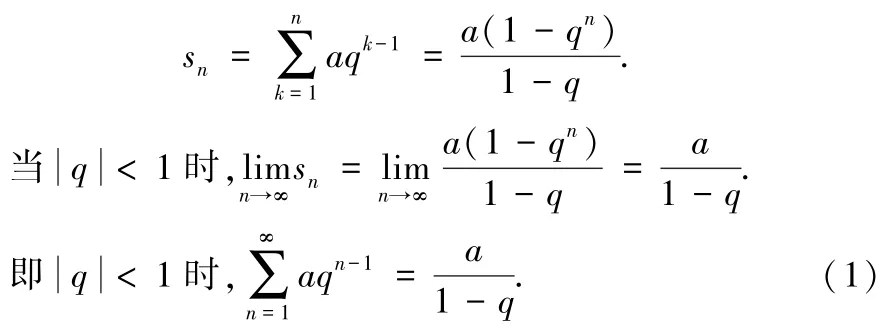
例1求級數的和.
解由上,此時
說明:只要等比級數滿足公式(1) 的條件,均可以用公式(1) 求和.
2.1.2 方程式法
方程式法是利用一些運算技巧對部分和數列構造方程表達式,進而得到部分和數列的和式表達,再取極限求得數項級數的“和”.
例2求數項級數的和.
解可以判定此級數是收斂且絕對收斂.設sn=1-
上面兩式相加有:
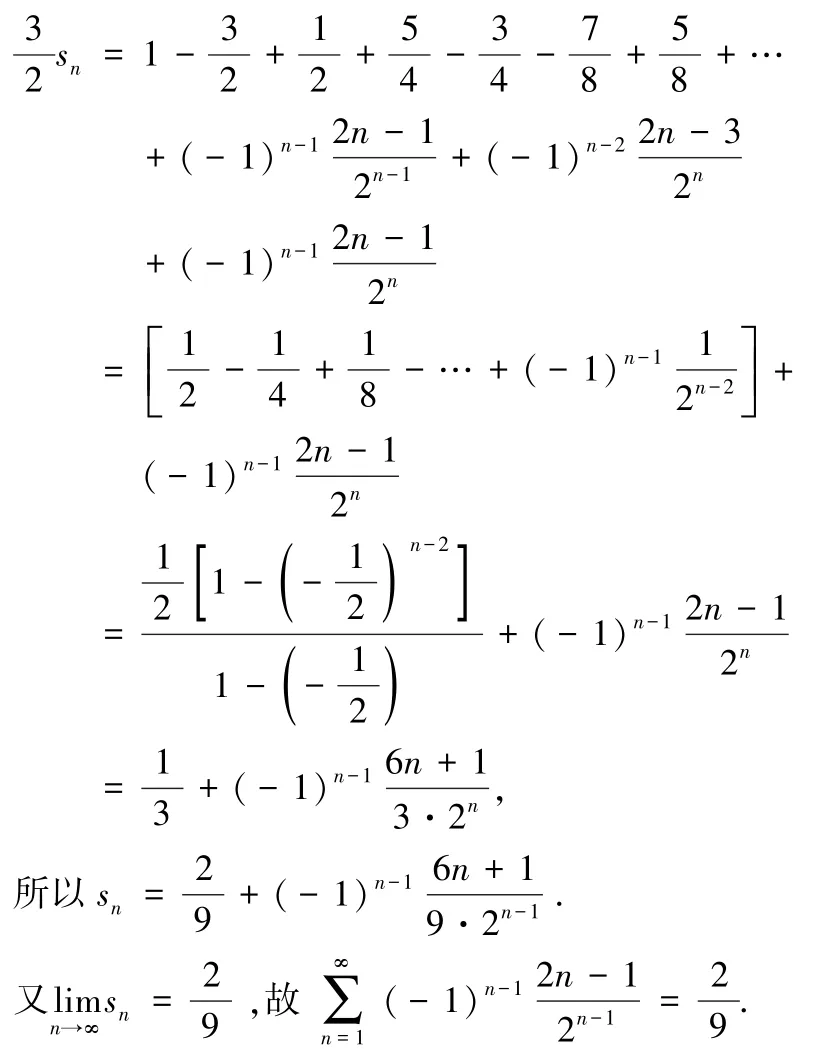
2.1.3 通項拆項法
通項拆項法是將數項級數的通項進行拆分,將部分和數列簡化后再取極限求數項級數的“和”.
定理1數項級數若un=an - an+1,且a,則
例3求級數的和.
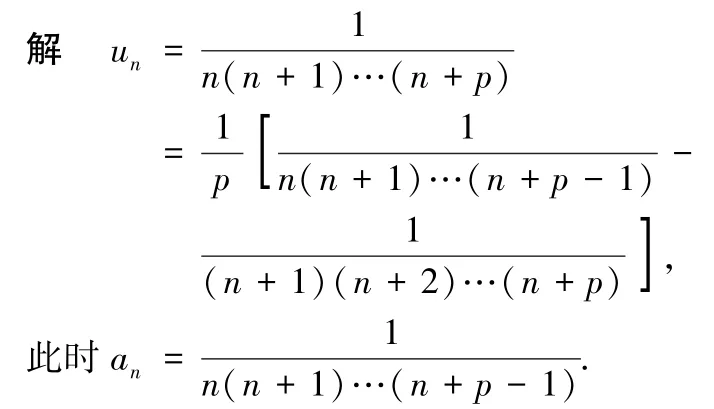
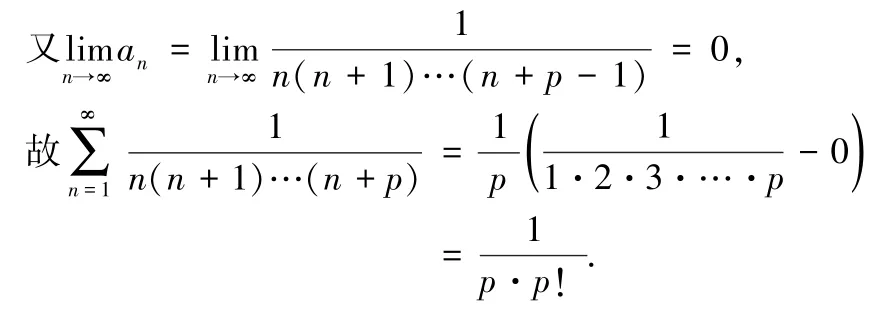
定理1 的一種變形為:
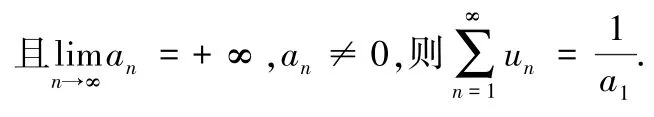
例4求級數的和.
解此時數項級數的通項
由an=n,且
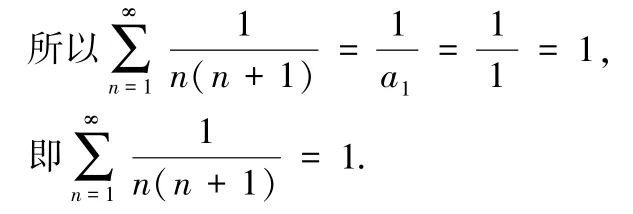
2.1.4 間接求和法
間接求和法是通過級數運算、級數性質將某些未知的數項級數表示為已知的收斂級數的線性組合,從而求得“和” 值.

2.2 利用冪級數求數項級數“和”
2.2.1 冪級數定值法
利用冪級數定值法的關鍵在于針對收斂的數項級數構造一個對應的冪級數.
例6求數項級數的和.
解構造形如的冪級數,當x= 3 時即為上述數項級數.
逐項求導,得
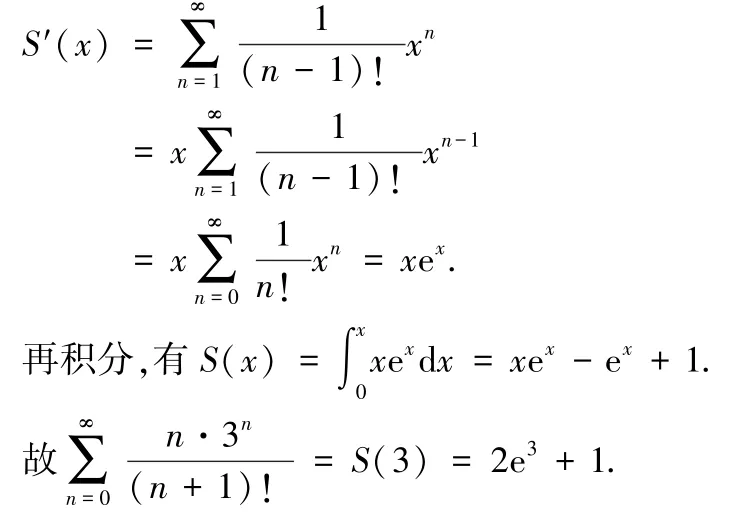
2.2.2 冪級數阿貝爾定理法
阿貝爾的冪級數連續定理:
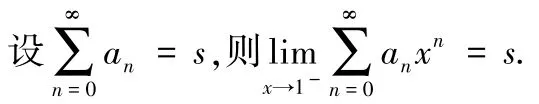
在應用阿貝爾定理求數項級數和時,首先要依據所給數項級數適當地設置一個冪級數,再求出此冪級數的和函數.定理表明和函數在x=1 處是左連續的,最后對和函數求極限,從而求出收斂數項級數的和.
例7求數項級數的和.
解構造冪級數其收斂區間是(-1,1].

2.3 利用傅里葉級數求數項級數“和”
nancosnωx0+bnsinnωx0,而x0是傅里葉級數展開式收斂區間的點,所以有此法也稱傅里葉級數的定值法.
例8求數項級數的和.
解將[-π,π]上的函數f(x)=x2做周期為2π 的周期延拓,并做傅里葉級數展開.
因為f(x)=x2為偶函數,
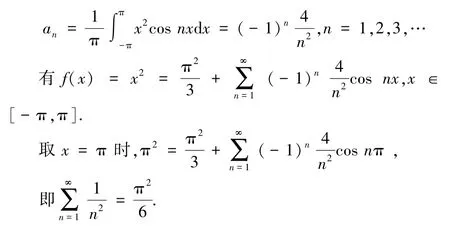
2.4 利用復級數求數項級數“和”
利用復級數求數項級數和的方法一般稱為三角級數法,主要是求級數的和,通常把它們視為復數域內的復級數此時z=eix, 然后對求和,并將其展成實部與虛部,則所求級數就是此復級數的實部與虛部對應的系數,從而求出“和”.
例9求的和.
解因為 cosnπ= (-1)n,n= 0,1,2,…所以
令z=eix,考慮復級數
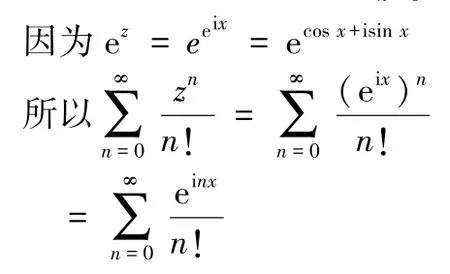
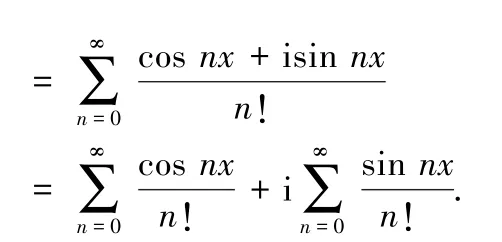
有 ez= eeix= ecosx+isinx= ecosx·eisinx= ecosx[cos(sinx) +isin (sinx)].
取x= π,得
3 結束語
求收斂的數項級數“和”是級數理論中的一個重點與難點,教學過程中因學時限制不能做系統地介紹,本文歸納和總結了一些典型的求“和”方法,主要涉及利用數項級數、冪級數、傅里葉級數及復級數的分析性質、和函數及函數的級數展開等對收斂的數項級數求“和”,有助于學生對級數理論的深入理解和提高.

