異質性條件下中國地區工業產能利用率的估測
——基于KLH模型和BC模型的比較分析

符 磊 李占國

(1.河海大學 商學院，江蘇 南京 211100;2.江蘇省社會科學院 泰州分院，江蘇 泰州 225300)

一、引言

自2008年金融危機以來，在外部市場沖擊與內在條件變化的交互作用下，中國經濟進入以中高速增長為特征的新常態。在這樣的背景之下，供需兩側矛盾集中爆發，產能過剩問題日益凸顯。2017年國際貨幣基金組織報告指出，產能過剩問題已經構成影響中國宏觀經濟穩定的重大風險。產能過剩橫跨公共和私人部門，牽涉十多個行業，存在于各個地區，對經濟體制改革、制造業高質量發展和區域協調發展構成嚴峻挑戰。2017年和2018年中央經濟工作會議先后強調，要繼續深化“供給側結構性改革”，以推動產能過剩問題化解，鞏固“三去一降一補”成果。作為供給側結構性改革五大任務之首的“去產能”，受到前所未有重視，但社會各界對于產能過剩治理政策及其效果卻存在一些爭論。

由于產能過剩問題的復雜性和長期性，對其治理陷入“屢調不止”(楊振，2017)和“久調不決”(徐朝陽 等，2015；朱希偉 等，2017)困境。目前，學界對于如何突破產能過剩治理困境仍未形成共識，存在較大分歧，具體表現在三方面。(1)產能過剩成因方面的分歧。現今產能過剩成因方面至少有三種代表性觀點，分別表現為：產能過剩主要由地方政府GDP競爭及特殊的政商關系等相關制度不完善導致的(耿強 等，2011；江飛濤 等，2012；朱希偉 等，2017)；對前景行業形成共同投資預期的潮涌現象所致(林毅夫 等，2010；林毅夫，2007)；市場失靈或是市場結構不成熟所引發(徐朝陽 等，2015；程俊杰 等，2015)。顯然，三種代表性觀點之間存在嚴重分歧，到底是市場缺陷導致，還是相關制度不完善導致，抑或是投資預期導致，并沒有形成定論。(2)產能利用率或產能過剩程度測算方面存在顯著差異。相關研究不勝枚舉，但測算產能利用率或產能過剩文獻仍然偏少，其中代表性文獻有：楊振兵等(2015b)測算2001—2011年中國工業整體的生產技術效率水平在63%～73%之間；劉京星等(2017)測算2001—2014年企業整體平均產能利用率為86.76%。現有文獻研究樣本的時間跨度基本相同，但產能利用率研究結論卻呈現顯著差異。(3)產能過剩治理的政策主張各有側重。制度不完善論者認為應以市場機制來消化產能過剩；潮涌論者強調投資信息的對稱性，即通過信息共享建立一致性預期以抑制投資沖動；市場論者主張更加積極地發揮政府治理過剩方面的作用，重點在于彌補市場不足。

基于不同產能過剩機理得到的研究結論和政策主張都存在一定的合理性，但缺少一般性和內在一致性。那么，能否找到一個統一的分析框架，將以上不同機理的產能過剩整合起來，找到彼此的聯系并進行合理界定呢？周勁等(2011)根據產能過剩發生機理將其分為周期性產能過剩、結構性產能過剩和體制性產能過剩，三類過剩特征不同，卻相伴而生為統一整體。周期性產能過剩的特征是隨著時間的變化而變化，與經濟周期具有協同性，這與潮涌現象所描述的過剩特征吻合；結構性產能過剩擁有較強的個體差異性，產生于供給匹配需求的矛盾中，與市場失靈和結構不完全導致的過剩特征吻合；而體制性產能過剩具有時間不變性、全局一致性及較強剛性，難以短期改變并在全國各地區幾乎同時存在。不過，僅僅進行理論上的歸納整合是不夠的，還須基于實證研究進一步驗證。

目前，測算產能利用率至少有六種方法：(1)用實際產出與設計生產能力之比來表示，Nelson(1989)利用該方法計算了美國私有電氣設施行業的產能利用率，該方法適用于少數企業或特定行業，適宜進行局部案例分析。由于具體企業產能采集數據工作量太大，且易于失真，故不適宜推廣到全部行業或進行宏觀層面全局性分析；(2)峰值法，也就是把生產水平顯著高于前后年的年份當作峰年，將實際產量與峰年產量對比測算產能利用率，這種方法易于處理但存在主觀性和系統性偏差；(3)數據包絡分析法(DEA)，該方法通常用估計企業的最大產出方式測算產能利用率，這一方法主要問題在于測算出來的數據區分度不大；(4)成本函數法測量，即以生產單元的歷史最優投入產出比為參照，將該時期的產量看作合適產出來測量產能利用率，孫焱林等(2017)利用該方法測算了中國2008—2014年間制造業全口徑分行業的產能利用率；(5)協整法，該方法避免了具體函數形式設定的不科學，消除了函數設定的主觀性造成的影響，但是相對于生產函數法和成本函數法，該方法忽略一定的微觀經濟基礎，同時也無法觀察不同生產要素之間的替代彈性；(6)根據隨機前沿分析預測行業的潛在產出水平，并計算產能利用率，該方法將生產函數、利潤函數或成本函數納入模型，同時引入符號受限的非效率誤差項，有效保證了模型的隨機性，成為眾多產能過剩實證研究的核心工具(楊振兵 等，2015b；程俊杰，2015a；程俊杰，2015b；楊振兵 等，2018)。綜上，當前并不缺乏研究產能過剩的實證文獻，但遺憾的是，并沒有統一框架下產能過剩的細分測度方法。

綜上，本文利用2003—2016年各省份規模以上工業企業數據，在Battese et al.(1995)構建的隨機前沿模型(以下簡稱BC模型)的基礎上，進一步使用Kumbhakar et al.(2014)的模型(以下簡稱KLH)并改進其設定，通過加入地區異質性并區分時變性和持久性非效率，以更好刻畫周期性產能過剩和體制性產能過剩，力求在統一框架下測度產能過剩。具體而言，本文有以下幾方面貢獻：第一，使用多誤差項隨機前沿模型，考慮地區異質性、時變性和持久性過剩來系統測度產能利用率，注重模型內部結構的剖析；第二，使用比較分析的思路，以經典的BC模型為參照，通過對比估計結果來詳細闡釋KLH模型下的測算結果，歸納產能過剩測算的基本事實，并討論BC模型對產能利用率低估的可能性和KLH模型測算的科學性。

二、文獻綜述

(一)產能過剩測度與隨機前沿面

國內測度產能過剩的代表性文獻中，楊振兵(2015)、楊振兵等(2015a、2015b)使用Aigner et al.(1977)和Meeusen et al.(1977)隨機前沿面模型測度產能過剩。程俊杰(2015a)基于Shaikh et al.(2004)的協整法測度產能過剩，程俊杰(2015b)基于Battese et al.(1995)的嵌入非效率項回歸方程的復合隨機前沿面模型測度產能過剩。上述代表性文獻所借鑒的方法都是經典隨機前沿面方法。

隨機前沿分析法(Stochastic Frontier Analysis, 簡寫為SFA)始于20世紀50年代估計生產函數的研究熱潮之中。具體看，生產函數刻畫的是既定投入與最大產出的技術關系，因此估計函數方程所收集的全體樣本觀測值需嚴格分布在小于最大產出的那一側，即只能接近或達到最優的“前沿面”卻不允許越界(Greene，1980)。Farrell(1957)將前沿面描述為產出包絡的一個等量線。這啟發了Aigner et al.(1968)的研究，即在保證殘差平方和最小化的前提下，使用二次規劃方法控制從模型中擬合而得的殘差，且限定其為負值，以此保證潛在最優產出一定可以大于實際產出，從而得到生產前沿面。但此時的模型沒有考慮隨機因素，故被稱為全前沿面模型(Full Frontier Model)。Aigner et al.(1977)(以下簡稱ALS)在此基礎上，首次引入誤差項組合結構：ε=u+v，其中，u代表不同樣本實際產出距生產前沿面的距離，即樣本間的產出效率差異，設定其服從截斷正態分布或者指數分布，v服從0均值同方差的正態分布，反映的是前沿面的隨機特征。ALS的貢獻在于首次引入誤差項組合結構，且詳盡計算兩者聯合概率密度函數，基于該函數可以利用極大似然法估計相應參數，從而獲得生產函數形式。由于生產函數和成本函數的對偶特性，隨機前沿分析也可以被用來估計成本函數，不過對于u的符號設定需要改變以刻畫表現為最小成本的前沿面。從Aigner et al.(1977)開始，隨機前沿面分析方法的基本思想和模型主體基本確定，后續研究在此基礎上進行創新和發展。

Stevenson(1980)進一步增強了SFA分析的一般性，其建立無需考慮u具體分布形態的估計模型，討論了均值不為0的一般情形，并設計了具體估計步驟。Jondrow et al.(1982)討論了包括u在內的誤差項復合結構整體的條件概率分布，從而測算出非效率的條件期望均值，并計算出不同樣本的非效率值。非效率的測算是隨機前沿分析的關鍵，非效率狀態的影響因素也值得關注。以產能過剩為例，過剩程度固然重要，其影響因素也同樣重要。比如，引進新技術工藝、加強需求信息收集、加大市場營銷力度和政府稅收相關政策等因素會顯著改變產能過剩狀態。Battese et al.(1995)、Huang et al.(1994)、Reifschneider et al.(1991)和Kumbhakar et al.(1991)較早關注以上問題，并建立包含不同非效率解釋變量在內的多方程隨機前沿分析模型。比如，Reifschneider et al.(1991)允許u作為非效率解釋向量Z的函數，即u=f(Z)。本文的BC模型就是Battese et al.(1995)在其研究中提出的嵌入非效率解釋變量的多方程SFA模型。

(二)BC模型與KLH模型

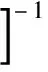
雖然Huang et al.(1994)、Reifschneider et al.(1991)以及Kumbhakar et al.(1991)的模型與BC模型在技術上非常相似，但BC模型卻更受國內學者歡迎。BC模型結構精巧易于理解，而且Battese et al.(1995)對Frontier4.1程序的運用方面論述詳細、步驟清晰。程俊杰(2015b)使用BC模型測算中國各地區的產能過剩，同時也使用Coelli編寫的Frontier4.1程序進行參數估計、檢驗與非效率計算。BC模型也被應用于其他與效率有關問題的研究(何楓 等，2004；符磊 等，2013)。這是國內學者認識較深刻且應用最廣泛的SFA模型之一，然而隨著SFA模型的發展，BC模型卻也至少存在以下兩個根本缺陷：

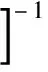
(2)BC模型中面板數據的異質性問題以及非效率中不隨時間變化的成分并沒有被充分考慮。BC模型的主體為：Yit=exp(xitβ+Vit-Uit)，其中，Vit是隨機擾動項，Uit為非效率項，設定為Uit=zitδ+Wit，即為uit=exp(g(t,T,Zit))|ui|線性形式。Wit為零均值常方差的服從截斷正態分布的隨機變量，其截斷點為-zitδ。問題在于，面板模型回歸中非效率項很可能會吸收地區異質性，形成對非效率的錯估，這一點BC模型完全沒有考慮到。Greene(2005)指出，非效率和截面異質性如果沒有得到有效區分，就會相互感染，進而存在嚴重錯估非效率的風險，應當在統一模型中分別加入兩者并進行區分和識別。

為了實現對BC模型的改進，相關研究進行了不同嘗試。Kumbhakar et al.(1995a)和Kumbhakar et al.(1995b)通過添加全新的非效率項組合來刻畫隨時間變化的非效率和不隨時間變化的非效率,即時變性非效率(Transient Inefficiency,以下簡稱TIE)和持久性非效率(Persistent Inefficiency,以下簡稱PIE)。但遺憾的是，這一嘗試沒有考慮截面異質性，因為截面異質性不隨時間變化的基本特性，也就被當作PIE進行處理，結果是PIE吸收了截面異質性，PIE被高估的同時，也高估了包括PIE和TIE在內的非效率整體。Wang et al.(2009)、Kumbhakar et al.(2005)和Greene(2005)雖對截面異質性與TIE進行區分，但卻忽視PIE的存在，比如Greene(2005)建立的真實隨機效應和真實固定效應模型就只考慮截面異質性，而沒有考慮不隨時間變化的那部分非效率。

可見，改進BC模型經歷了一個試錯過程，以上兩類研究都未能綜合考慮截面異質性、PIE和TIE，沒有能真正彌補BC模型的缺陷。真正實現BC模型改進的是KLH模型，KLH模型是指Kumbhakar et al.(2014)文獻中所使用的SFA分析模型，其對截面異質性與非效率進行了有效區分，并將非效率進一步細分為PIE和TIE，以此建立綜合隨機前沿模型，這被稱之為KLH模型，其基本結構為：ln Yit=α0+γxit+μi+vit-ηi-uit。相較于BC模型，KLH模型具有以下三個方面優勢：第一，刻畫更多非效率項，各部分度量更加精確，總體更加全面和科學；第二，既容納了個體異質性，又考慮了長期性產能過剩的存在，并在同一框架下對兩者進行了清晰區分和測度；第三，模型蘊含的重要假設是個體在時間t的TIE與其前期的TIE不相關，這考慮了理性經濟主體會及時解決那些短期可以解決的非效率問題，從而使得效率得以提升。

需要說明的是，Colombi et al.(2014)在有效區分異質性、PIE和TIE基礎上，做了與KLH模型相似的貢獻，兩者區別在于估計技術上的差異。本文的KLH模型僅特指Kumbhakar et al.(2014)所使用的模型，并不包括Colombi et al.(2014)的研究模型。由于KLH模型對BC模型存在實質性改進，有鑒于此，BC模型將作為本文的參照模型，用來與KLH模型估計結果進行對比。本文在綜合考慮地區異質性的前提下，細分測度長期性產能利用率和時變性產能利用率，通過比較兩類模型測算結果，指出特定時期有關中國各地區工業產能利用率的基本情況。

三、BC模型

(一)變量和數據

(1)工業產值。工業產出通常選擇工業總產值或工業產值增加值。由于本文計算產能利用率的回歸模型本質是生產函數，即研究工業總產出與資本存量、勞動投入的關系，最終選擇工業產值而非工業增加值代表產出水平。國家統計局自2013年起不再提供分地區的工業總產值數據，僅有工業銷售產值和存貨數據，本文使用工業銷售產值加上存貨價值表示工業總產值。具體地，我們查找國家統計局分省份年度數據庫中的規模以上工業企業經濟指標數據，存貨數據已經更新到2018年，但銷售產值數據只更新到2016年，因此只能獲得各地區2003—2016年工業總產值，同時將工業銷售產值作為工業產值的替代變量，以便后續進行穩健性檢驗。同時，為去除價格因素影響，查找國家統計局公布的各省份同期工業生產者出廠價格指數。以2003年為基年，對以后各年的名義工業總產值進行價格指數平減，得到不變價工業總產值，然后取自然對數得到總產出變量ln Y的數據。

(2)資本存量。對于資本存量，根據國家統計局分省份數據庫中規模以上工業企業經濟指標數據，選擇規模以上工業企業固定資產合計數據作為資本存量，并以規模以上工業企業資產總計數據作為替代變量，以便后續進行穩健性檢驗。具體地，查找2003—2016年各省份規模以上工業企業固定資產合計數據和資產總計數據，同時為消除價格因素影響，查找同期各省份固定資產投資價格指數，以2003年為基年，對名義凈值進行平減而得到實際固定資產凈值，然后取自然對數得到回歸模型中的ln K。

(3)勞動投入。對于勞動投入變量，本文選擇規模以上工業企業平均用工人數，數據來源于《中國工業經濟統計年鑒》。由于《中國工業經濟統計年鑒》缺少2012年各地區的該類數據，這里使用了牛頓插值法，根據其他年份的數據對2012年數據做內插處理。經過不同的參數選擇及結果比較，最終決定利用2009—2011年、2013—2015年的數據內插出2012年相關數據。最后對各年的數據取自然對數，得到回歸模型中的ln L。

(4)非效率方程的相關變量。地方政府干預程度(GVE)，參考程俊杰(2015b)的做法，使用地方政府一般財政預算支出占GDP的比重表示；國內市場需求因素(MDF)，使用地方最終消費占GDP比重表示；外部需求因素(TDF),使用地方對外貿易總額占GDP比重(即貿易依存度)表示；經濟波動因素(EWF),使用HP濾波分解出實際GDP的波動項來表示。

本文工業產值、資本存量和勞動數據樣本為2003—2016年中國分地區規模以上工業企業數據，數據來源為國家統計局和當年的《中國工業統計年鑒》，并根據同年的《中國工業經濟統計年鑒》數據做補充。由于西藏自治區部分年份數據不完整，故而剔除，共得到中國大陸不包括西藏在內的30個省級行政區域的面板數據。非效率方程的相關數據變量來源于各地區各年度的統計年鑒和國家統計局網站。

(二)模型和估計結果

基于BC模型，我們建立如下回歸方程：

ln Yit=α0+γ1ln K+γ2ln L+γ3(ln K)2+γ4(ln L)2+γ5(ln Kln L)+

γ6t+γ7t2+γ8tln K+γ9tln L+vit-uit

(1)

uit=δ0+δ1GVE+δ2MDF+δ3TDF+δ4EWF+wit

(2)

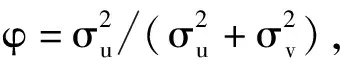
表1 BC模型估計結果

BC模型采用了嵌入式的非效率方程結構，必須先檢驗模型的設定是否合理，具體通過三步來進行。首先，根據以上結果，我們檢驗v-u結構中u是確定性變量還是隨機變量。令原假設為φ=0，回歸結果顯示，φ=0.71，t統計量為8.62，在0.01顯著性水平上拒絕原假設，故認為φ≠0，u是隨機變量，這是BC模型應用的前提條件，否則嵌入式的非效率方程將無法存在。其次，需檢驗非效率項u是否為非效率方程中GVE、MDF等變量的線性表示，確定非效率線性方程總體是否顯著，即檢驗δ1=δ2=δ3=δ4=0。通過回歸我們發現，GVE、MDF、TDF和EWF同時進入非效率方程時，非效率項的各變量皆不顯著，由于第一步檢驗已經排除了非效率為非隨機變量的可能，考慮GVE、MDF、TDF和EWF存在共線性問題，通過逐步排除，最終保留GVE和TDF兩個變量，GVE參數顯著為正，而TFD參數顯著為負，非效率方程的結構進一步優化，即在無法拒絕δ1=δ2=δ3=δ4=0時，我們重新設定非效率方程，試圖檢驗δ1=δ3=0的原假設，非效率方程變為uit=δ0+δ1GVE+δ3TDF+wit。最后，檢驗模型是否可直接使用OLS估計。如果φ=δ0=δ1=δ3=0，那么BC模型的誤差項中的結構v-u并不存在，同時非效率方程也不存在，模型“退化”為一般的線性模型，可以直接使用OLS進行估計。關于δ1=δ3=0以及φ=δ0=δ1=δ3=0為原假設的檢驗，BC模型給出了一種檢驗方法，即通過構造似然比統計量并證明該統計量服從混合卡爾方分布(Mixed chi-square Distribution)，具體的統計量構造公式為：λ=-2(log(likelihood(H0))-log(likelihood(H1)))，likelihood(H0)和likelihood(H1)分別為原假設和備擇假設成立時的對數似然值。相關檢驗結果見表2，表明模型采用當前形式較為合理。可以進一步測算產能利用率，BC模型測得產能利用率數值見表3，圖1則直觀展示了各年份平均產能利用率的變化趨勢。

表2 似然比統計量檢驗

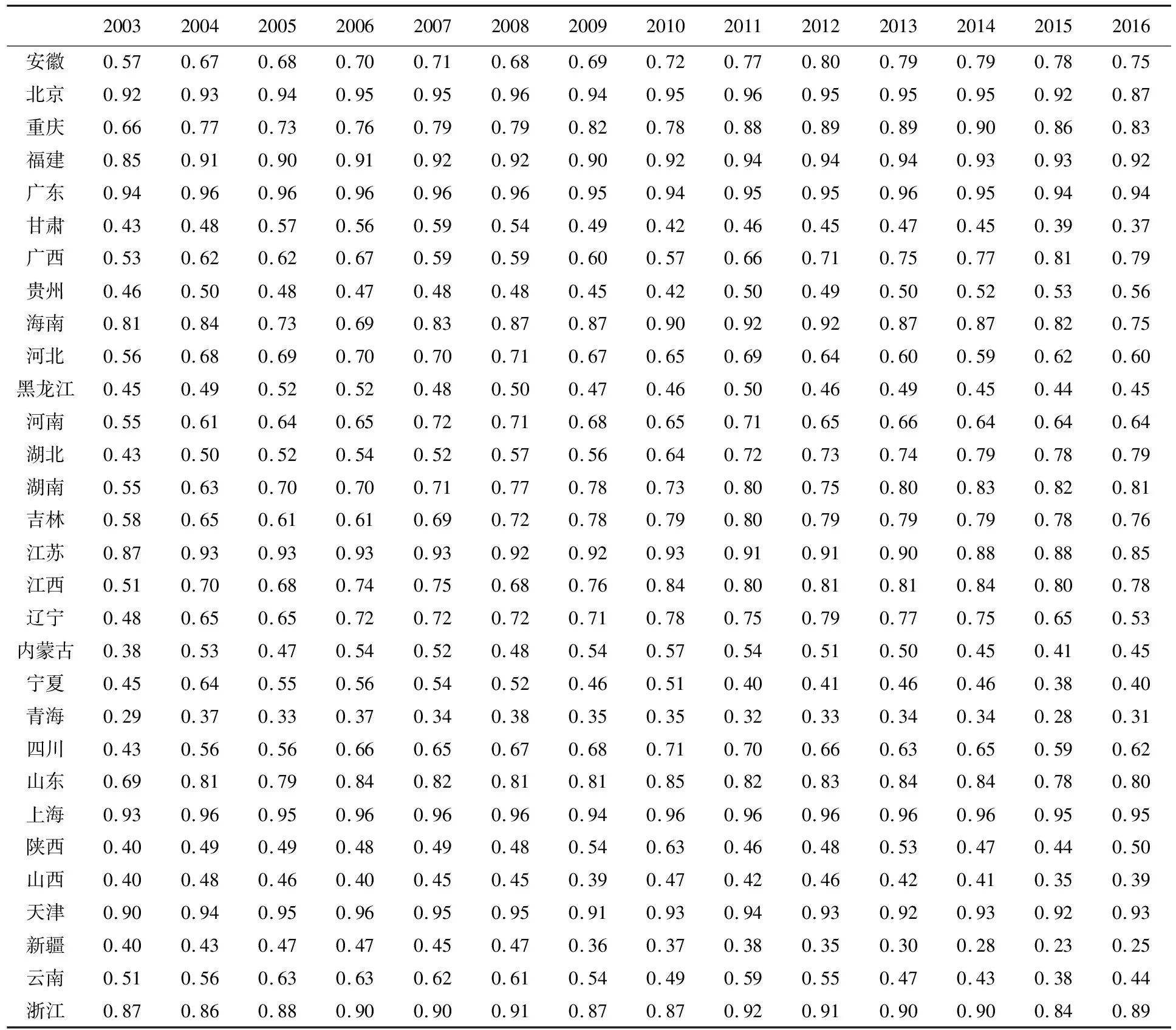
表3 BC模型測算的產能利用率

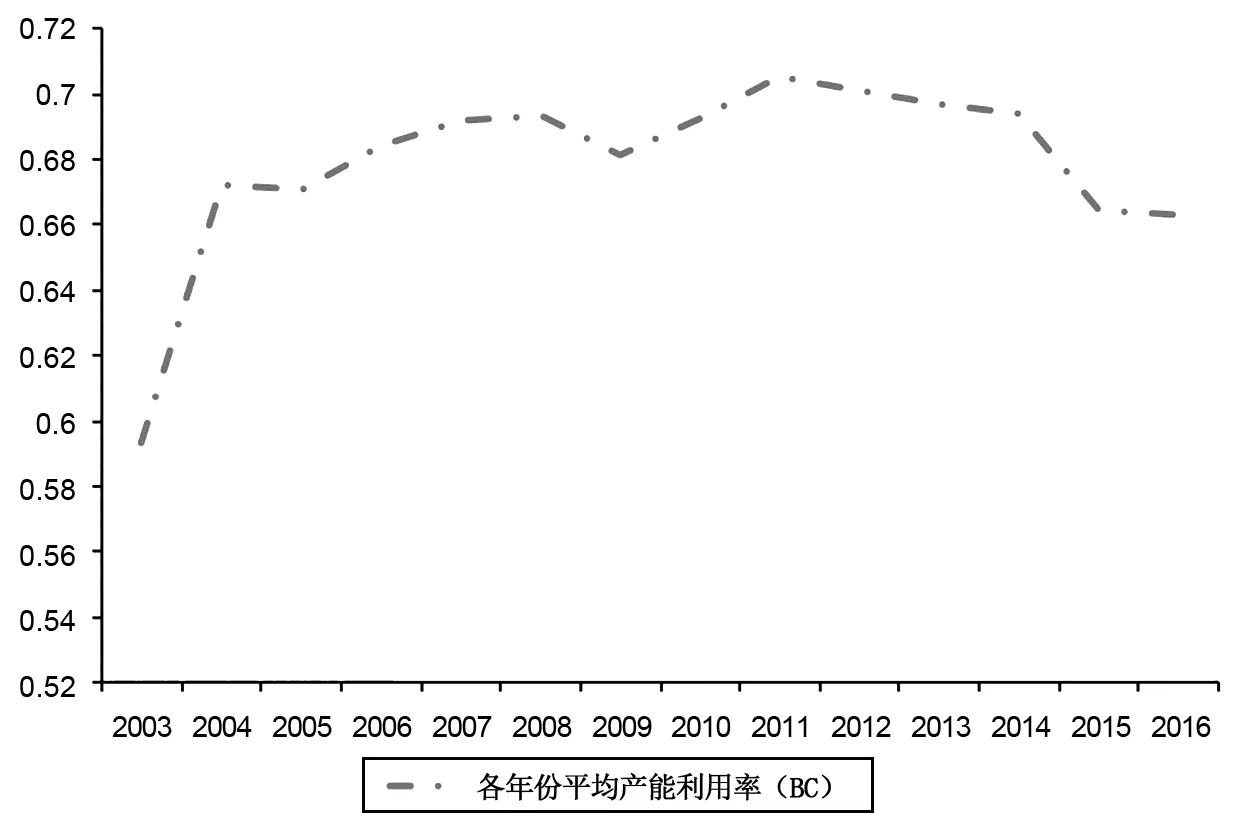
圖1 BC模型各年份平均產能利用率

四、KLH模型

(一)模型結構

按照Kumbhakar et al.(2014)的設想，將截面異質性與非效率之間關系的兩類研究思想進行融合，這既考慮截面異質性，又考慮PIE和TIE，以此來建立綜合的隨機前沿模型。在考慮技術應用趨勢論述的基礎上，本文使用生產函數的超越對數形式表現模型主體部分，具體如下：

ln Yit=α0+γ1ln K+γ2ln L+γ3(ln K)2+γ4(ln L)2+γ5(ln Kln L)+

γ6t+γ7t2+γ8tln K+γ9tln L+μi+vit-ηi-uit

(3)

具體到產能過剩問題，以TIE表示時變性產能過剩，PIE表示持久性產能過剩。產能過剩的反面是產能利用率，為便于分析，使用以下幾個概念：時變性產能利用率(Rate of Transient Capacity Utilization,簡稱TCU)、持久性產能利用率(Rate of Persistent Capacity Utilization,簡稱PCU)以及綜合產能利用率(Rate of Comprehensive Capacity Utilization,簡稱CCU)。

(二)測算步驟

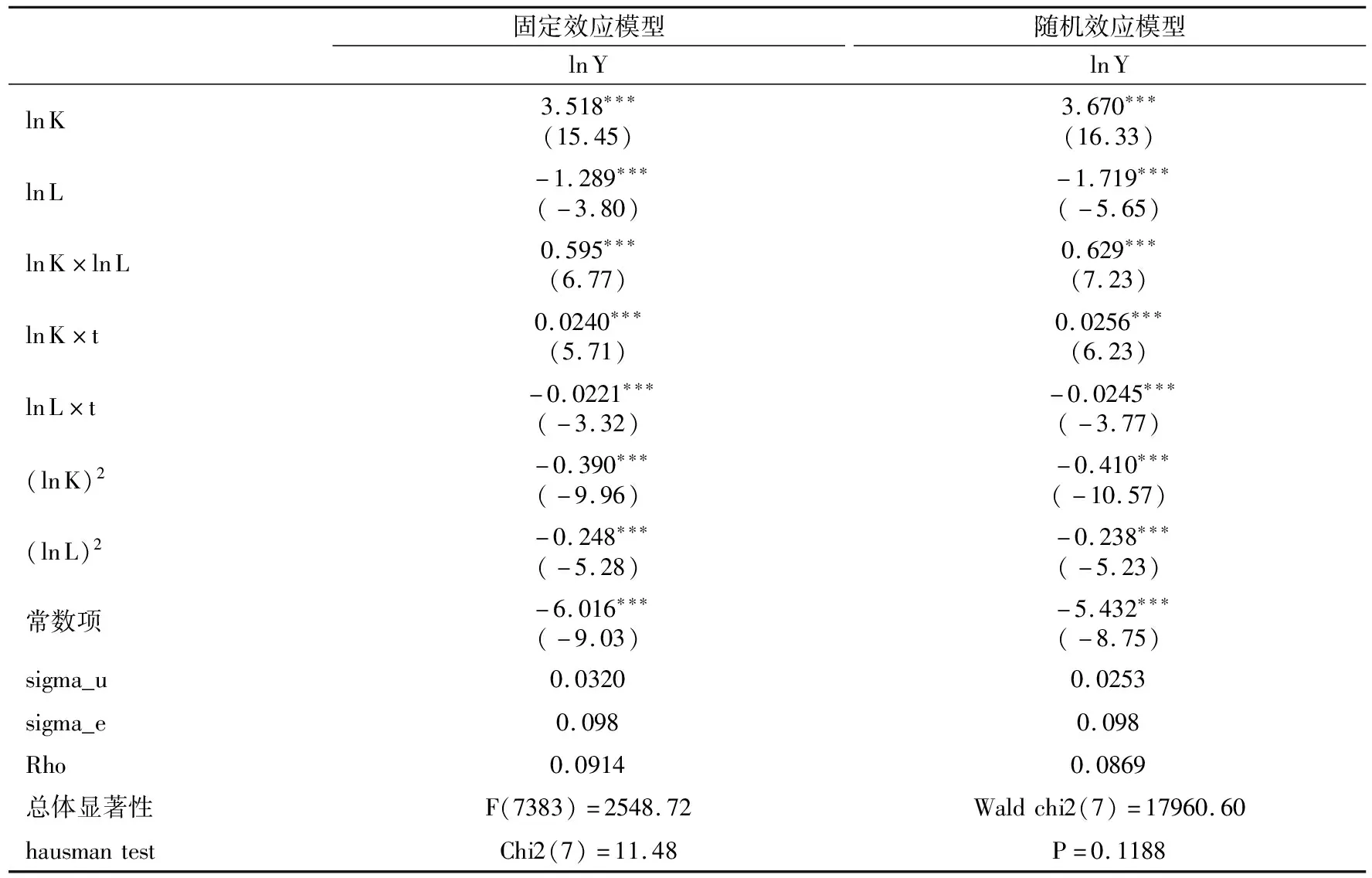
表4 基礎面板數據模型回歸結果

表和的描述性統計量

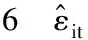
表正態性檢驗結果

(4)

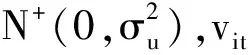
(5)

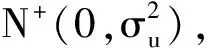
(6)

而vit的概率密度函數為：

(7)

由于uit和vit相互獨立，據此可進一步確定τit：

(8)

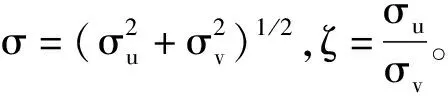
式(5)代入到式(8)，可得：

(9)

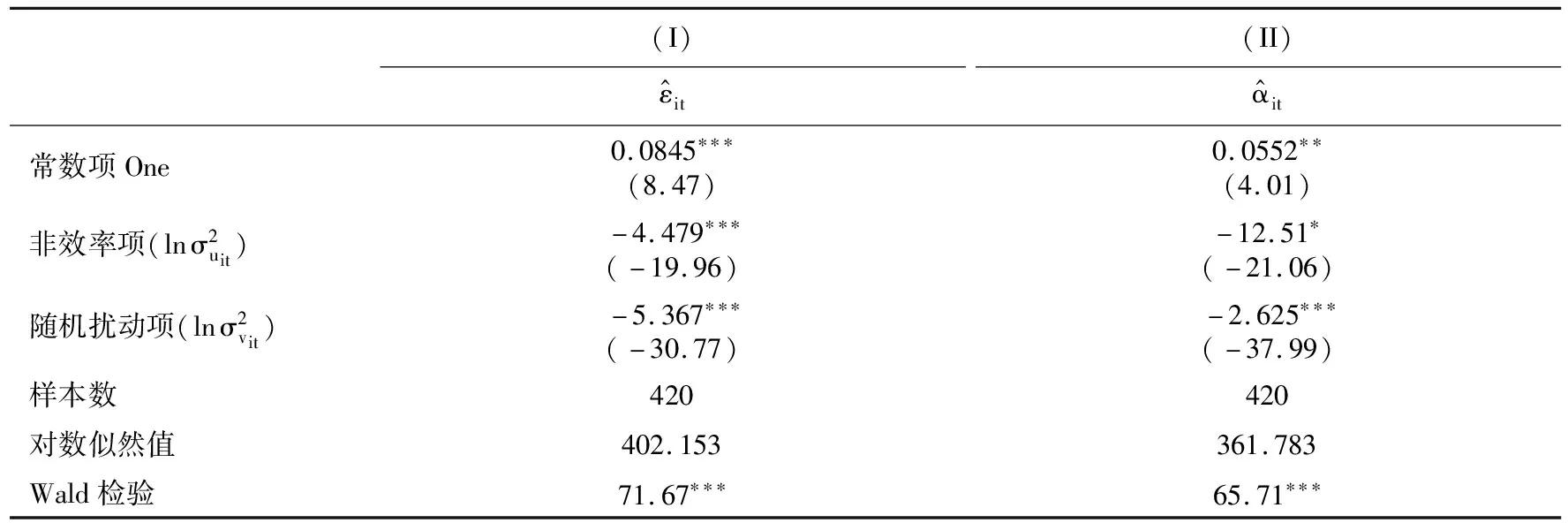
表7 隨機前沿面模型回歸結果

表測算結果

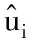
表9 各地區異質性指標測算結果

表10 PIE測算結果

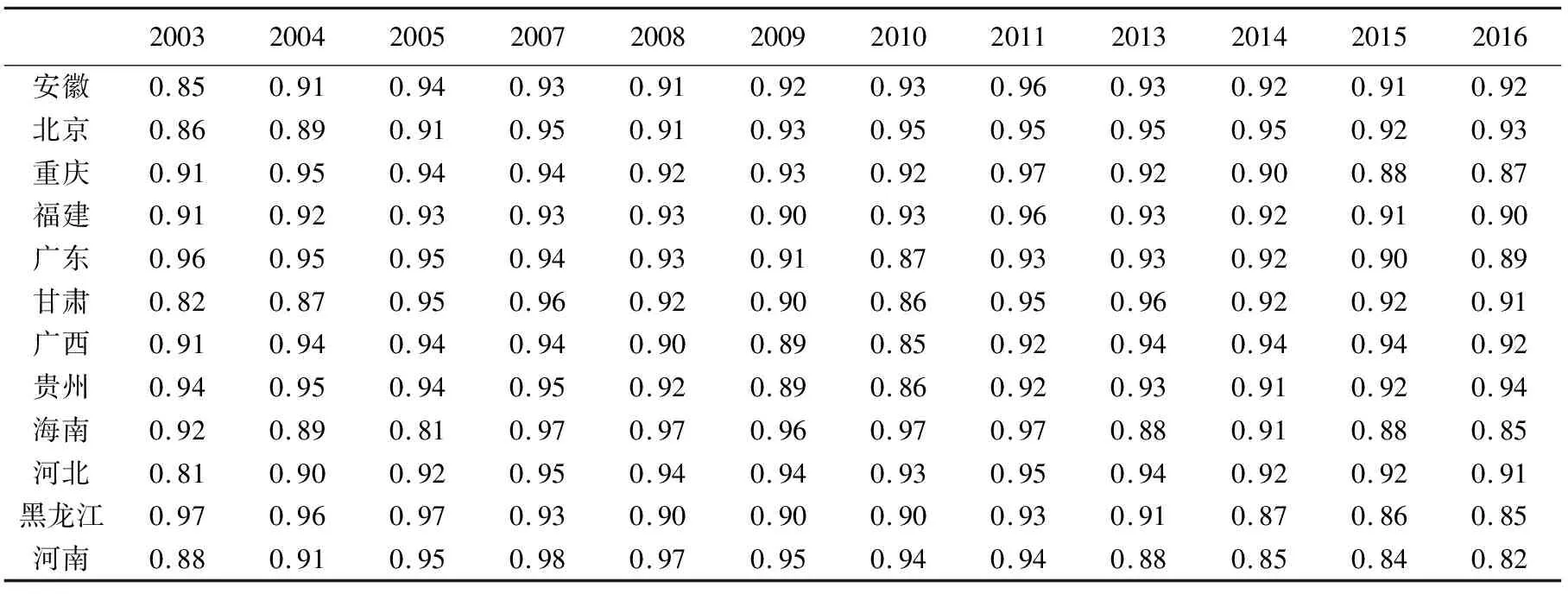
表11 綜合產能利用率CCU測算結果

表12 各類產能利用率測算結果的描述性統計

圖2表示30個省份各年份平均的TCU、PCU以及CCU。整體上，各年份的PCU接近于1，表明長期性非效率導致的產能利用率不足雖存在，但比重極小。TCU在69%～98%之間，是CCU的主要組成部分，表現為CCU與TCU呈現高度一致，這說明TCU不足是CCU不足的主要原因。

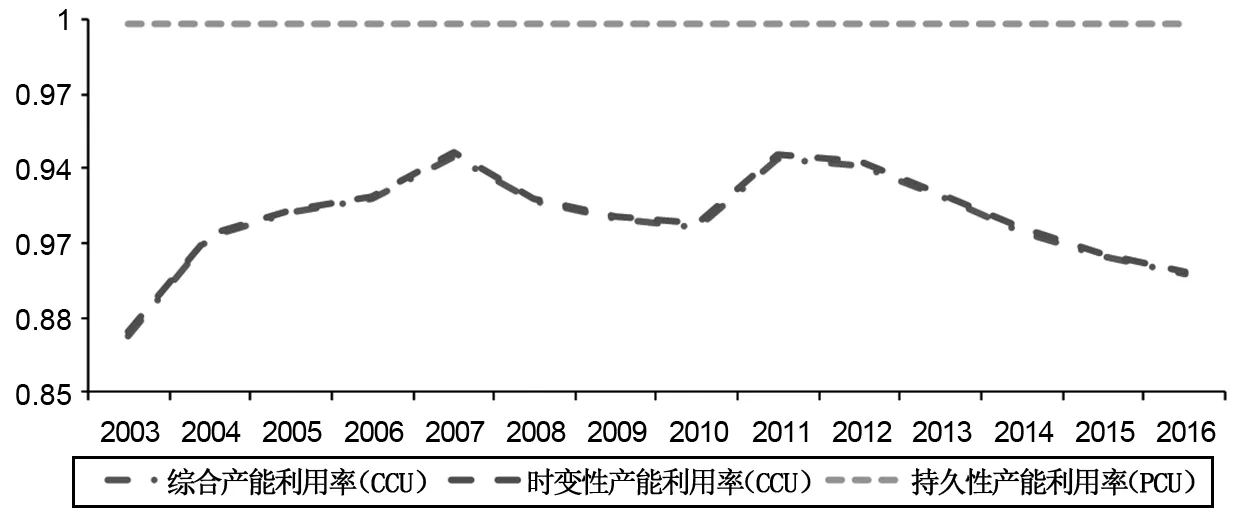
圖2 平均產能利用率時間趨勢

本文的測算結果與程俊杰(2015a,2015b)、楊振兵等(2015b)的結果存在一些差異，具體表現在：第一，本文綜合性產能利用率的測算結果均值約為0.92，高于前述研究結果；第二，由于隨機誤差項的存在，各樣本與前沿面都存在一定差距，無法達到甚至超過前沿面，本文的測算結果不存在大于1的數值，也沒有等于1的數值；第三，本文的測算結果包含時變性與持久性產能利用率，也包含這兩種產能利用率相結合的綜合性產能利用率；第四，本文測算的綜合產能利用率走勢與國家統計局抽樣調查法的走勢基本保持一致，在2007年和2011年這兩個年度是產能利用率的高點(見圖3)，其他相關研究則是呈現出2003年之后產能利用率不斷下降的趨勢(既沒有在金融危機沖擊下出現大幅下降，也沒有“4萬億”投資刺激存在短暫反彈)。本文的測算結果則清晰地展示了這些特殊事件的沖擊。

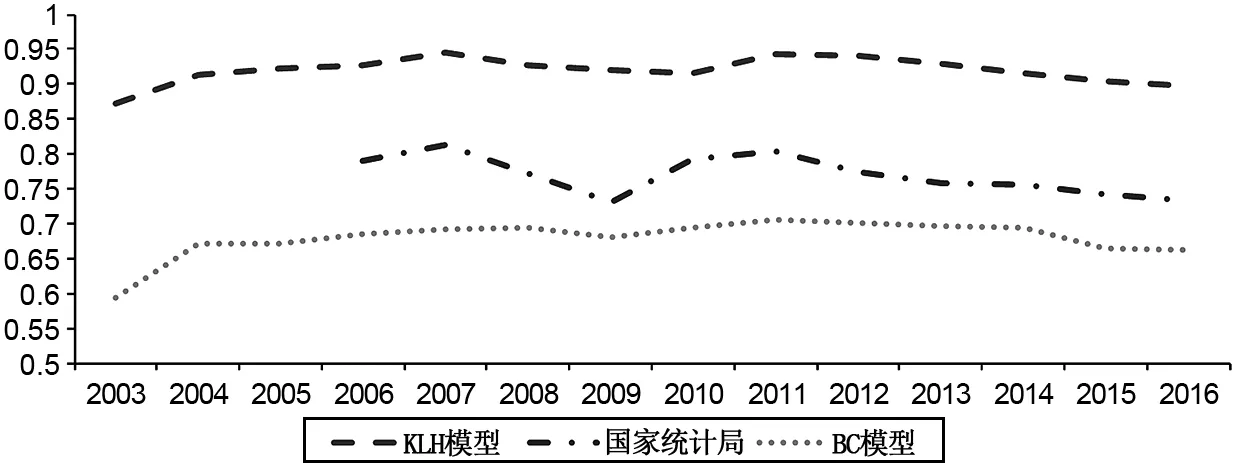
圖3 KLH模型、BC模型測算結果與國家統計局統計調查結果的對比

雖然這些差異的產生與數據、變量選擇有一定關系，但最主要的原因在于本文的實證分析中區分了地區異質性、時變性和持久性產能過剩。由于剝離地區異質性，使得影響產能過剩因素中較少摻雜其他雜質，而不再被高估。地區異質性在KLH模型中實際就是地區技術水平的差異，如果該差異沒有被考慮，而用相對發達地區的技術水平去衡量欠發達地區，無異于否認地區間發展不平衡的現實。KLH模型的測算結果表明，從各地區自身的生產前沿面來看，規模以上工業企業的產能過剩并沒有想象中那么嚴重。但需要注意的是，2011年以來產能利用率一直處于下降趨勢之中，產能過剩問題仍然存在。此外，本文使用的是規模以上工業企業數據，而規模較大企業的產能利用率一般相對較高(1)徐朝陽等(2015)對此就有很好說明，即隨著行業成熟和不確定性減少,優勢企業會不斷擴大規模,逐步淘汰劣勢企業,最終形成較合理的市場結構和產能利用率。，這也很好地解釋了本文測算結果較先前研究要高的原因。

(三)穩健性檢驗

為檢驗KLH模型的穩健性，我們使用各地區規模以上工業企業銷售產值代替工業總產值作為產出變量，用規模以上工業企業資產總計代替固定資產總計數據作為資本投入變量，其余變量保持不變，以檢驗基礎面板數據模型各變量的參數符號是否發生偏轉，估計結果如表13所示。表13估計結果表明，各參數符號沒有發生任何偏轉。唯一變化的是，變量ln L×t的參數不再顯著，變量(ln L)2的參數能通過0.1顯著性水平檢驗，其余變量均能通過0.05顯著性水平檢驗，表明不論是隨機效應還是固定效應模型，都具有比較好的穩健性。

表13 穩健性檢驗下的基礎模型參數

在基礎回歸后，通過hausman檢驗確定使用隨機效應模型進行進一步估計。為節約篇幅，相關步驟結果不再重復交代，而是直接給出綜合產能利用率CCU、時變性產能利用率TCU和持久性產能利用率PCU的描述性統計。穩健性檢驗下CCU和TCU的均值變動在1%左右，結果可以接受(見表14)。KLH模型測算的產能利用率相對形態也幾乎無變化(見圖4)，表明效率測算的最終結果也存在較好穩健性。

表14 穩健性檢驗下各類產能利用率的描述性統計

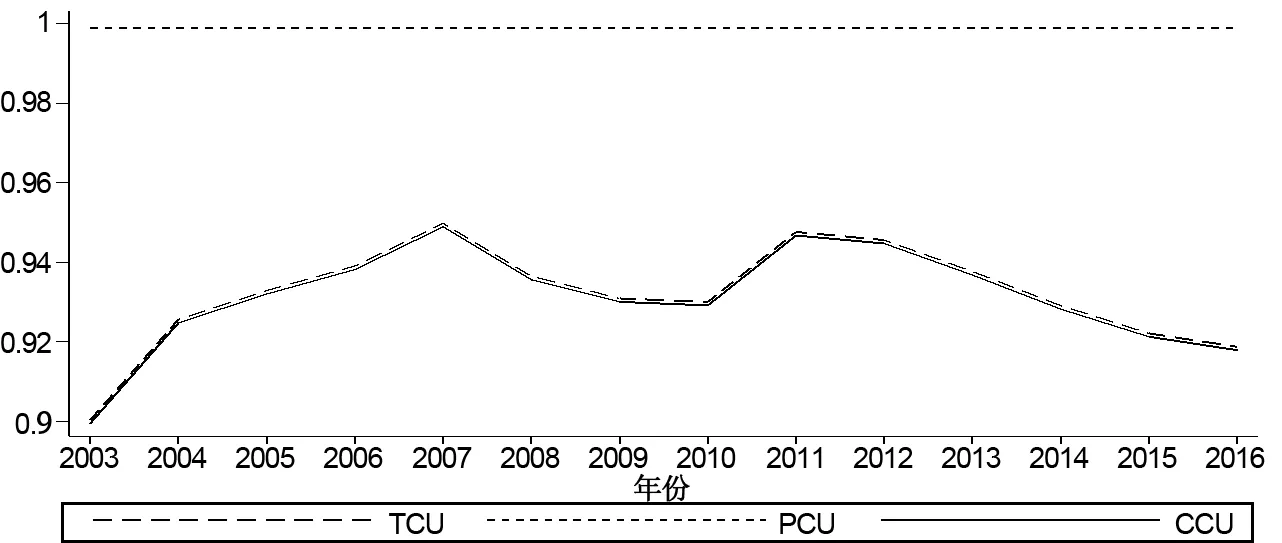
圖4 穩健性檢驗下KLH模型的產能利用率形態

五、兩種模型測算結果的差異

(一)潛在差異分析

由于BC模型忽視地區異質性，未能區分時變性非效率和持久性非效率，使得產能過剩被高估，這是一種系統性偏差，也是BC模型的內生缺陷。另外，持久性非效率和地區異質性之間容易混淆，即便考慮了地區異質性，但若未能有效區分持久性非效率和時變性非效率，那么異質性也會吸收持久非效率項，使得非效率被低估，從而產生系統性偏差。我們在使用模型測算產能過剩時，過剩產能中的短期過剩產能和長期過剩產能都不難理解，那么地區異質性又是什么呢？具體又如何區分地區異質性和非效率呢？Greene(2005)指出，各地區真實潛在的生產函數包含不容易觀測的地區個性特征，反映出使用生產技術本身的差異而不是效率差異。換言之，面板數據下模型選取的具體函數形式是不完全的，在完全的生產函數假設下不存在技術差異，只會存在效率差異。由于BC模型測算結果未考慮地區異質性，相當于忽視了客觀存在的地區技術差異，僅注意到不充分問題而忽略了不平衡問題。而KLH模型加入對地區異質性考量，在考慮客觀存在的技術差異基礎上進一步區分時變性和持久性過剩產能，測度產能過剩要更加科學。

地區異質性是使用KLH方法的關鍵，測算中國不同省份的地區異質性對于理解各地區產能過剩十分重要，我們已經在表9中給出了測算結果。通過計算地區異質性指標也可集中反映樣本時段內各地區在技術差異方面的大致狀態，為求直觀，將測算結果繪制在圖5中。通過比較發現，海南、天津、北京、上海等地區異質性指標為正，這些地區絕大多數為東部地區省份，但也有內蒙古、青海、云南等西部地區省份，說明樣本時段內這些地區的技術先進性特征明顯；而中部地區江西、安徽、河南、湖南和湖北的地區異質性指標皆為負，說明技術水平始終處于相對較弱地位，技術先進性欠缺；部分西部地區省份由于受國家政策扶持，在樣本時段內獲得技術水平較先進產業的集聚，這些地區因承接高技術產業而獲得后發優勢，地區技術先進性水平較高。

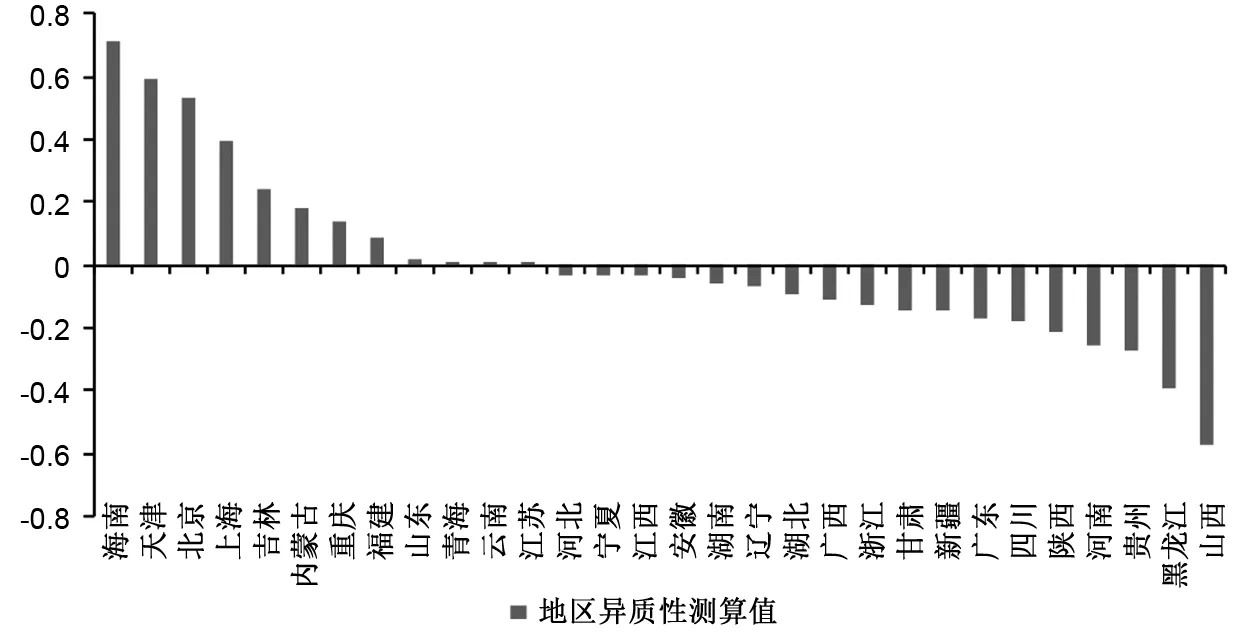
圖5 各省份地區異質性測算值比較

(二)具體差異分析

1.總體差異

第一，KLH模型測算結果的年均值在87.3%～94.5%之間，而BC模型測算結果每年均值在59.3%～70.6%之間。由此可見，KLH模型測算結果明顯高于BC模型測算結果。2003—2016年，均值差異最大的年份為2003年，復雜誤差項結構模型測算結果為87.3%，BC模型測算結果為59.3%，相差28.0%；差異最小的為2014年，復雜誤差項結構模型測算結果為91.5%，BC模型測算結果為69.4%，相差22.1%；其他年份差異值均在24.1%上下波動。第二，KLH模型測算結果中，2003年產能利用率最低，2007年產能利用率最高。BC模型測算結果同樣是2003年產能利用率最低，但產能利用率最高年份卻是2011年。第三，兩種模型的測算結果雖然差異性顯著，若在各年份對每一地區產能利用率取均值，揭示產能利用率地區均值的時序波動趨勢，則發現兩種測算結果的波動趨勢十分接近，具體見圖3。

從模型優劣對比角度來分析以上三方面總體差異：第一，KLH模型測算結果總體比BC模型測算結果高，正如前文理論分析可知，BC模型未能有效甄別地區異質性，從而造成過剩產能被高估，產能利用率被低估，這符合我們的預期；第二，KLH模型與BC模型的測算結果差別不僅僅在于系統性偏差，還在于模型中各部分誤差被識別時模型內部相對差異發生變化，這就造成了兩種測算結果雖然都確認2003年為各自內部的產能利用率低點，但各自的高點卻不相同；第三，兩種測算結果雖然存在系統性偏差和內部相對差異，但他們所顯示的產能利用率地區均值時序波動趨勢基本相同，這說明兩種隨機前沿模型在測算產能利用率時所得到的結果一定程度可以相互印證，但這種印證是相對意義而非絕對意義上的。2003—2016年中國各地區產能利用率基本呈現一種扁平的“M形態”，這恰巧也與國家統計局調查數據相吻合。這進一步說明，在隨機前沿分析框架下，對各地區產能利用率測算得到的相對狀態存在一定程度的統一，不同模型的測算結果差異主要體現在絕對差異方面。

2.地區差異

第一，根據KLH模型測算結果可知，2003—2016年間平均產能利用率最低的地區為廣西，最高是天津；而2003—2016年BC模型測算的平均產能利用率最低的省份為青海，最高為上海。進一步按西部地區、中部地區和東部地區排列發現，BC模型測算的產能利用率存在西部地區、中部地區、東部地區逐漸提升的“階梯爬升”狀態(見圖6右圖)，而KLH模型測算的產能利用率呈現“東西兩端高、中部低”狀況，類似于一種“懸鏈”狀態(見圖6左圖)，而且東部地區高于西部地區。這里再次強調，BC模型是基于同一技術假設，即以東部地區技術水平衡量中西部地區，此時中西部地區產能過剩很可能處于被夸大的狀態。而KLH模型不僅考慮地區異質性，還區分了時變性和持久性非效率。KLH測算結果表明，中國的產能利用率呈現東部地區、西部地區、中部地區依次下降的空間格局，中部地區才是產能過剩最為嚴重的地區。

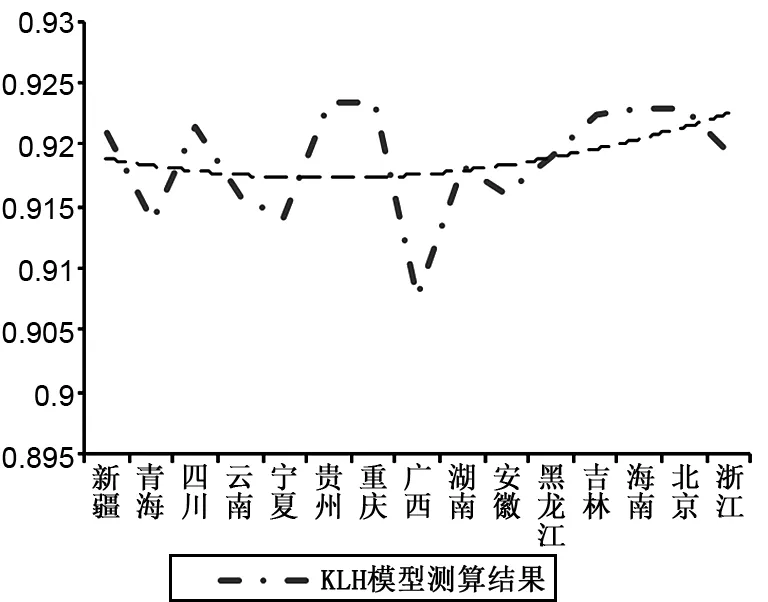
圖6 兩種模型測算結果時間均值的截面圖

第二，有別于各年份的差異性，KLH模型測算結果雖大部分高于BC模型測算結果，但是天津、北京、上海及廣東四個省份的BC模型測算結果卻高于綜合產能利用率的測算結果(見圖7)。而用兩種方式測算出來的省份數據差異中，青海的差距最大，相差了57.8%，福建差距最小，僅有0.6%。這再次驗證了一個邏輯，即BC模型測算下產能利用率高的地區一定是發達地區或者技術先進地區，而技術相對落后地區的產能利用率一定很低，因為這完全是忽視地區異質性的結果。

圖7 兩種模型時間均值的截面對比

第三，若單看圖7，KLH模型測算的各地區產能利用率時間均值幾乎沒有差別。但放大來看，上海、北京、廣東等地依然處于產能利用率排名靠前的位置，而廣西、河南、內蒙古、新疆等地區依然處于產能利用率排名靠后的位置。比較KLH模型和BC模型測算結果來看，排名靠前的地區和排名靠后的地區雖然沒有完全一致，但存在較高重合度。廣東在BC模型測算結果中排名僅次于上海，在KLH模型中排名僅次天津；青海在BC模型排名中倒數第一，但在KLH模型排名中倒數第五(見圖8)，這些都充分體現了BC模型與KLH結構模型在測算中存在的具體差異。

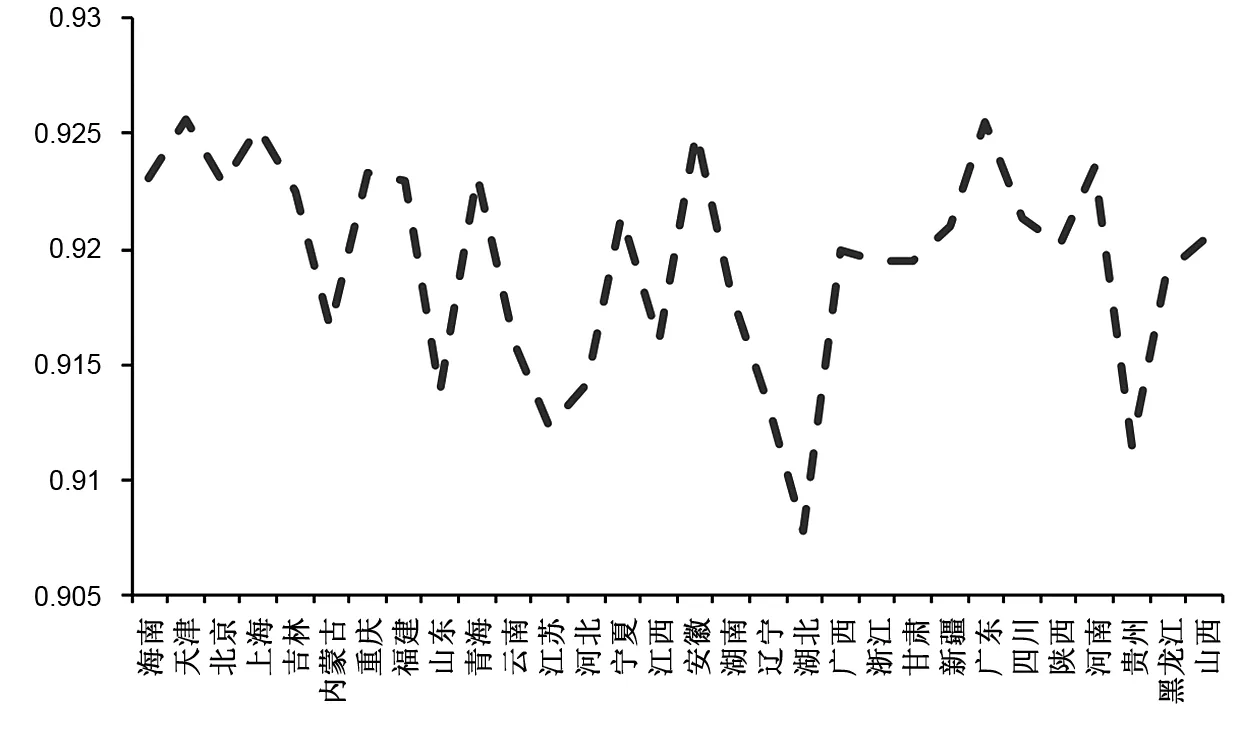
圖8 KLH模型時間均值的截面形態

出現以上差異基本符合理論預期，且與實際情況相符。上海整體的技術先進性毫無疑問應該居于全國前列，KLH模型的地區異質性指標也印證了這一點(見圖5)。對于非效率的定義，Colombi et al.(2014)有明確界定，在一定投入下樣本個體未能達到代表最大產出的隨機前沿面的距離，即為一定技術下的非效率。一個地區技術與效率往往具有強關聯性，但這并不代表二者完全等同。技術水平高的地區效率并不一定高，原因在于市場的根本矛盾是供需矛盾，而不是生產矛盾。生產水平高、需求不足的情況下，效率不可能太高。回到KLH模型，上海的地區異質性指標為0.398947(見表9)，是個正值。BC模型沒有考慮地區異質性，導致非效率項(2)非效率項是SFA模型中對-Uit的統稱。Uit一定需要交代符號，在生產函數型SFA中，如果使用Vit-Uit的結構，Uit一定需要為正，本文就是這種情況。結合本文研究的問題，Uit在本文表示的就是過剩產能。(-Uit)吸收了正的地區異質性(μi)，使得該地區的過剩產能被低估，同時高估其產能利用率，這可能也是BC模型對上海產能利用率估計值大于KLH模型估計結果的原因。同樣地，BC模型測算結果中，天津、北京同上海一樣產能利用率偏高，可能同屬經濟發達技術先進地區，地區異質性指標分別為0.594269、0.533983。

不過，BC模型中上海的平均產能利用率最高，但其地區異質性指標并非所有地區最高，這表明除了地區異質性外，還有其他因素會影響產能利用率的數值。廣東的情況恰好說明這一點，其地區異質性指標為負(見表9)，但BC模型測算的產能利用率同樣高于KLH模型結果。據此可以推斷，地區異質性在數值較大時會顯著影響BC模型估計結果，即正值較大時將會造成過剩產能顯著被低估，負值較大時將會造成過剩產能顯著被高估，而絕對值接近于0時將不再明顯。廣東地區異質性指標為-0.16753，地區異質性是影響過剩產能估計的重要因素，但并非唯一因素，隨機擾動項的影響以及 BC模型錯誤設定使得常數項吸收了部分異質性或持久性非效率，即被BC模型識別的非效率較小，從而形成一定程度的估計偏差。

六、總結與討論

本文使用BC模型和KLH模型分別測算2003—2016年中國各地區規上工業企業產能利用率，并對實證結果進行了對比分析。通過對比發現，應用KLH模型與BC模型測算產能過剩的差異在于：(1)測算邏輯差異。BC模型假設所有截面具有相同技術，以此測算各截面、各時點產能過剩程度；KLH模型則是承認截面存在不同技術，并在此基礎上測算各樣本產能過剩程度。前者是尋找最高技術水平，并將其作為衡量所有樣本的準繩，而后者是對不同地區設定符合其技術水平的標準，以此標準度量地區各時間點上產能過剩情況。(2)測算結果差異。BC模型測算的產能利用率較低，KLH模型測算產能利用率較高。這是因為前者設定標準較高，自然導致測算的整體水平較低；后者設定標準根據各地區具體情況而定，測算值的整體水平較高。產能過剩問題無疑需要從各地區生產能力實際出發，以先進地區的生產能力來衡量落后地區沒有意義。(3)測算置信度差異。KLH模型本身就是BC模型的升級，其具備以下兩個方面特點：一是可區分時變性產能利用率和持久性產能利用率；二是充分考慮地區異質性，從方法上而言，KLH模型要更先進，使用相同數據時測算結果要更可靠。

基于兩種模型的測算結果，關于2003—2016年各地區規上工業企業產能過剩程度，至少存在如下幾個方面可以肯定的基本事實：(1)使用BC模型測算的產能利用率結果，除處于技術前沿的少數地區樣本外，大部分地區的產能利用率必然存在一定程度被低估；(2)中國東部地區的規模以上工業企業產能利用率相對較高，中西部地區則相對較低，中部地區和西部地區孰高孰低并不確定；(3)2011年以來各地區產能利用率逐漸下降，產能過剩風險逐漸加大；(4)2003年以來，產能利用率存在“兩次升高、兩次降低”的趨勢。

另外，通過對比也發現一些值得推敲的地方。第一，KLH模型測算的產能利用率是否符合現實，其值在69%～98%之間，年均值在87.3%～94.5%之間是否科學?一方面，真實的規模以上工業企業產能利用率水平肯定要大于BC模型測算水平，這一點我們已經進行了討論。不僅如此，如果規模較大，企業產能利用率水平較高的假設成立，那么規模以上工業企業產能利用率一定會大于國家統計局通過抽樣調查獲得并公布的數據。這是因為，國家統計局統計調查范圍是大中型企業，對“小微企業”抽樣調查會使產能利用率降低。從這一點看，KLH模型測算結果較為科學。另一方面，作為隨機前沿面模型，KLH模型估計技術存在改進空間，變量的選取優化和模型的校準可能帶來更加精確的測算結果。第二，通過分解時變性產能利用率和持久性產能利用率發現，時變性是關鍵。我們基本可以認定的是，不隨時間變化的那一部分產能過剩微不足道，而隨時間變化的產能過剩則是主要的部分。造成產能過剩三大原因中，周期性原因具有強時變性特征，體制性原因具有強持久性特征，結構性原因在兩者之間。由此可以推斷，當前產能過剩更多是周期性和結構性原因而非體制性原因。不僅如此，體制恰恰是我們應對產能過剩的優勢，這也是各地區產能利用率一直還比較理想的重要原因。